中国の有名な機械学習の本の勉強ノート。自分がわからなかったところだけなので飛び飛びだろう。
全結合層だけで構築すると、以下のような問題が生じてしまう。
- パラメタが多すぎる 入力画像が100*100*3なら、入力層から隠れ層への写像で、1つの隠れ層のニューロンごとに、100*100*3=30000個の入力が入り、それぞれに1つ重みが必要なので30000個のパラメタが生じる。隠れ層のニューロンを増やすとこれが簡単に増えてしまい、訓練が遅いばかりか、高すぎる学習能力による過学習も生じてしまう。
- 局所的な特徴を捉えられない 画像認識の例でいうならば、画像の拡大縮小回転反転平行移動などは全部同じものだと認識してほしい。ただ、全結合層だけで作ると、各場所におけるパターンそれぞれが全部必要となってしまい、面倒なdata augmentationが必要なばかりか訓練もかなり大変になる。
生物学的に受容野は網膜などの上の局所的=一部の場所の周辺の信号のみ受容するという性質を持つ。この局所的な特徴を捉えるのを意識したネットワーク構造が、Convolutional Neural Networkである。
畳み込み(Convolution, 卷积)
一次元の畳み込みの例
一次元の畳み込みの例として、信号処理でよく用いられる。信号の列に対して、減衰を考える。時間1では1倍、時間2では0.5倍、時間3では0.25倍のように各信号ごとに時間によって減衰を考える。これはであるとおく。(これはFilterやConvolution Kernelと呼ばれたりする)
この時、時刻における信号を考える。
このように、総和や積分の中で、パラメタを動かしているとき、添え字とが互いに掛け合わせているものが、一次元の畳み込みである。
一般的に、畳み込みは以下のようにあらわす。先ほどのはの1点のみの畳み込みだったが、すべてについて行うとすると、同様なベクトルが得られる。
二次元の畳み込みの例
同様に、二次元の畳み込みも定義できる。の画像に対して、フィルタの畳み込みを行うとき、以下のようになる。
畳み込みを行った結果、となる。
なお、数学的には畳み込みは互いに交換可能である。
画像処理などでよく使われるmean filterなどはすべての値が同じフィルタを使って平均を取っている。例えば、フィルタの一例。
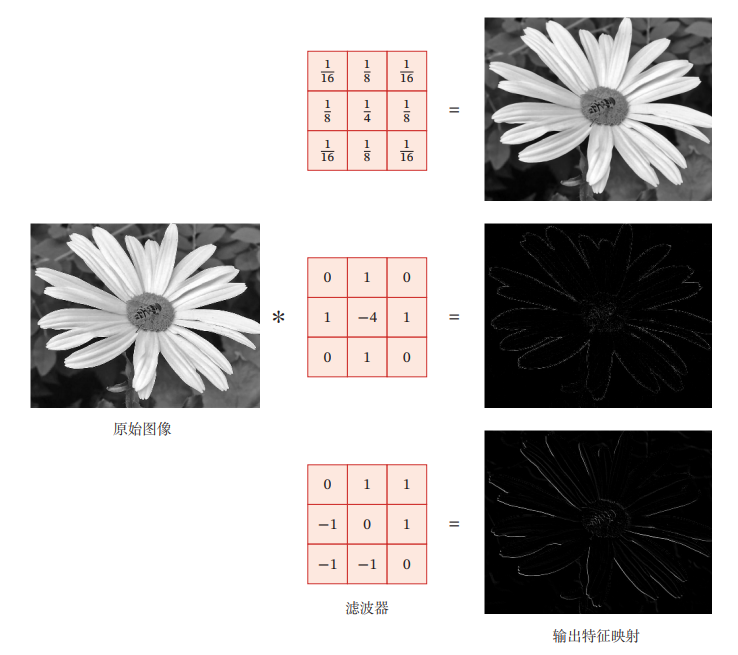
CNNでは、このフィルタ自体を機械学習によって学ぶというもの。
Cross-Correction
なお、畳み込みの順序を真逆にすることによって、フィルタとの似てる度を測定できる。内積みたいな感じで。これはCross-Correction=相互相関関数という。
StrideとPadding
Strideは畳み込みで、毎indexごとに増やす数。普通は1。Paddingはエリア外を0埋めすることによって、畳み込みしても元のデータとサイズが変わらないようにするためのもの。
入力はで、フィルタサイズは、ストライドはだとする。よくあるやり方の例としては以下の通り
- Narrow Convolution 畳み込み後はとなる。
- Wide Convolution 畳み込み後はとなる。
- Equal Width Convolution 畳み込み後はのまま。
- これよく見る気がする。
なお、一般的には畳み込み後のサイズはである。
CNN
畳み込み層
全結合層では、であった。畳み込み層では代わりに、以下のようになる。
これによって過学習の原因となる大量のパラメタを減らすことができ、真に有意義のようなパラメタだけを残すことができる。
畳み込みの性質上、1つのフィルタに対して決められたストライドで動かして畳み込んでいくので、複数のフィルタによって複数個の特徴をつかみたいのであれば、複数の畳み込みフィルタを用意する必要がある。
具体的に画像について述べると、のデータが与えられる。は色の次元数でRGBの三色なら3。
畳み込みフィルタはの次元に対して、のサイズで畳み込みを行う。つまり、全体では、のフィルタは、個存在している。(はフィルタの数である つまり実際はフィルタの数に深さを乗じたもの個のフィルタが存在することになる)
この場合、畳み込みした結果も当然行列が個存在することになる。
プーリング層(Pooling Layer, 聚汇层)
畳み込み層によって、特徴抽出における重みのパラメタ数は劇的に減少したが、畳み込みの結果の行列は個存在しており、サイズ不変のまま畳み込んだとしたら、次の層への入力はとなり、次の層への入力は大きいままである。
これをダウンサイジングするにあたって、全結合層でやると結局大量の重みを抱えてしまう。そこで、の中での各ブロックに区分し、その中から計算を施し、1つだけ値を出力してそれだけを残すという作業を考える。これはプーリングという。
よく使用されるプーリングは二種類存在する。
- Max Pooling 対象の中で最大の値を選択する。
- Mean Pooling 対象の中の平均値を取る。
これによって、画像の全体的な構図大きく損なうことなく、特徴量を減らすことができる。
CNNの全体的な構造
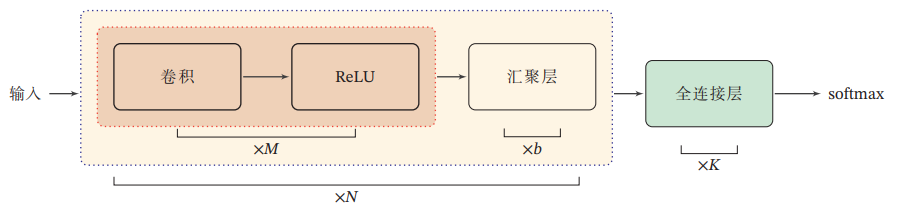
パラメタの更新の理論的な部分はスキップだ。
有名なCNNアーキテクチャ
CVの識別タスクなどで、高い性能を(その時点で)出したSOTAモデルたちの中で、技術のブレークスルーを導いたもの。基本的に論文でも、ベンチマークの基準として使用されている。
LeNet-5
1998年に提案された。入力は32*32のサイズの白黒画像であり、10カテゴリへの分類。(手書き数字の分類)
- 畳み込み層。の画像から、で畳み込みを行い結果としてなので、の畳み込んだ結果が6つ得られる。(はフィルタの数)
- でMax-Poolingを行い、が6つに抽出する。
- 畳み込み層。で畳み込みを行い、結果としてなので、の結果が個の存在する、かと思いきやより相互依存を強く仮定することで上手く削減して個の結果としている。
- 2と同様なことをする。が16個得られる。
- 畳み込み層。。この時結果としてはまで縮めた120個のスカラーが得られる。
- 全結合層+出力層 10個にまとめる。
AlexNet
2012年に革命(かぜ)を起こした深層CNNモデル。現代のCVでも活用されているテクすなわち、GPUで訓練し、ReLU関数を活性化関数として使い、Dropoutで過学習を防ぎ、Data Augmentationも行った。
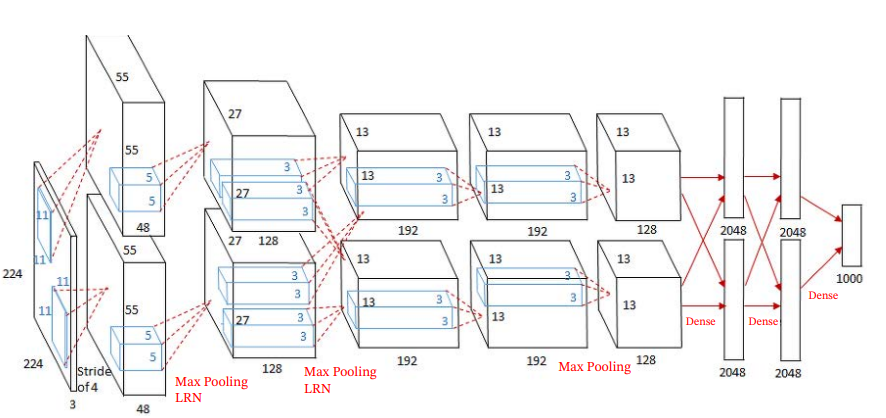
入力画像はであり、出力はカテゴリ。
赤い部分はすべてででMax-poolingを行っていて、サイズを落としている。落としてから、畳み込みをしている。
途中で2つの部分で交叉する畳み込みは、それぞれの部分(上下)から1回ずつ畳み込んで次の結果を作っている。
Inception
1つの畳み込み層に、複数のサイズのフィルタを許容しているのをInception Modelという。
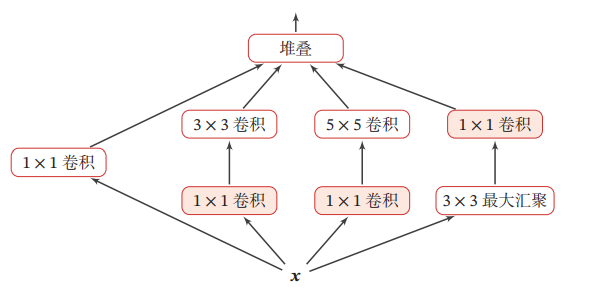
複雑でSequentialでなくなっている。
- 左から1番目は、で畳み込み
- 左から2番目は、で畳み込んでから、で畳み込み
- 左から3番目は、で畳み込んでから、で畳み込み
- 左から4番目は、でMax-poolingしてから、で畳み込み。
- そして上の4つの結果をすべてflattenして1つのベクトルにする。
2014年のImageNet分類コンテストを制覇したGoogLeNetはInception Modelである。勾配消失問題を解消するため、中間層で2つの補助分類器を導入しているらしい。
ResNet
Residual Network、残差ネットワークと呼ばれる。
識別器を使って、を近似したいと考える。このとき、関数を恒等関数と残差関数に分解することができる。実際、後者を学習させる方がずっとやりやすい。恒等関数は次図のように、そのまま持っていくことができるので、勾配消失に強いのである。
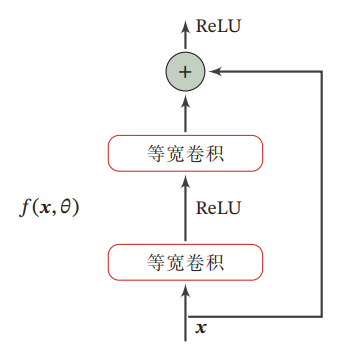
以上では、サイズを変更しない畳み込み→ReLU→サイズを変更しない畳み込みによって、残差を近似させる一方で、はそのまま持っていく。
他の畳み込みの方法について
主に、転置畳み込み、アトラス畳み込みの2つがある。
転置畳み込み(转置卷积)
通常の畳み込みは次元を落とすのが普通だが、低次元から高次元に写像しつつ、畳み込みをしたいときがある。
次のように畳み込みの重みをずらして配置することで、実現は可能。
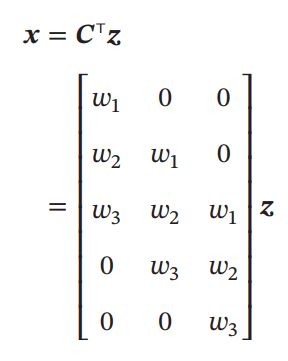
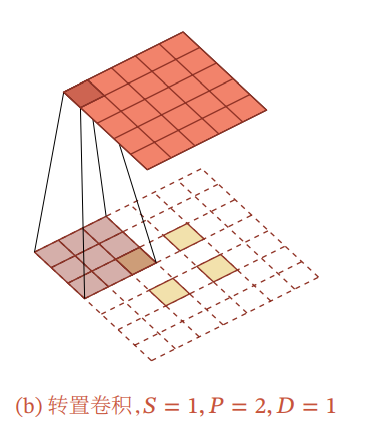
Fractionally-Strided Convolution(微步卷积, 小数点ストライド畳み込み)
の小数点のストライドで畳み込みを行う。各特徴量の行列の成分の間には0を挟むことによって、影響させないようにする。
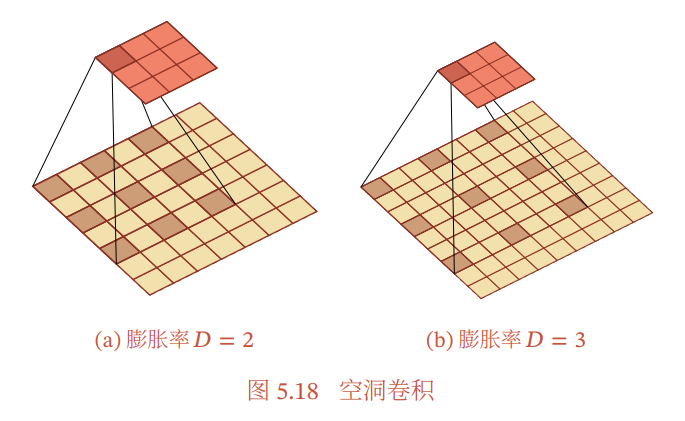
Atrous Convolution(空洞卷积, 空洞畳み込み)
元の間に0を挟むらしい。上と同じじゃね?Paddingの取り方で違うとか