NNDL 第10章独立した複数のモデルの訓練による効用

中国の有名な機械学習の本の勉強ノート。自分がわからなかったところだけなので飛び飛びだろう。

https://nndl.github.io/

Ensemble Learning Bagging AdaBoost Self-trainingとCo-training Self-training=Bootstrapping Co-training Multi-task Learning Transfer Learning(迁移学习)Inductive Transfer Learning Fine-tuning Transductive Transfer Learning Covariance Shiftについて Continuous Learning(Lifelong Learning)Elastic Weight Consolidation Fisher Information Matrix どのように使うか Meta-Learning(元学习)Optimizerベースの学習モデルに依存しないMeta-Learning

複数のモデルを別々に訓練して、これらで協力などをしながら最終的に決定を下すという手法は一般的にはかなりに有効である。この章では各種のこのような手法について触れている。

Ensemble Learning

複数の学習器の出力結果をうまく使って、予測の正解率を上げる手法。

一番簡単なのは単純平均をとること。 $M$ 個の識別器がそれぞれ $f_1, \cdots, f_M$ だとする。単純平均は以下の通り。

F(\mathbf{x}) = \frac{1}{M} \sum_{m=1}^M f_m(\mathbf{x})

単純平均による期待誤差は、以下のように評価できる。真のモデルは $\mathbf{y}=h(\mathbf{x})$ とする。

\epsilon_m(\mathbf{x}) = f_m(\mathbf{x}) - h(\mathbf{x}) \\ R(f_m) = \mathbb{E}_{\mathbf{x}} [\epsilon_m(\mathbf{x})^2] \\ \bar{R}(f) = \frac{1}{M} \sum_{m=1}^M R(f_m) \\

$F(\mathbf{x})$ の期待誤差は、 $[\frac{1}{M} \bar{R}(f) , \bar{R}(f)]$ に収まるという定理が得られる。どのようにやっても、期待値の $1/M$ 倍から1倍の間を動くということ。

証明

各識別器の期待誤差平均がわかっているとき、単純平均すると以下のように2乗のかたちになる。

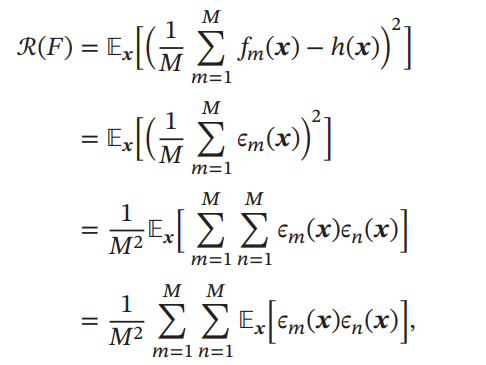
2行目から3行目は、2乗を展開し、畳み込みを明示的に見つけられる。 $\mathbb{E}_{\mathbf{x}} [\epsilon_m (\mathbf{x}) \epsilon_n(\mathbf{x})]$ は2つの識別器のそれぞれの誤り率である。

各 $m \neq n$ について $\mathbb{E}_{\mathbf{x}} [\epsilon_m (\mathbf{x}) \epsilon_n(\mathbf{x})] = 0$ であるときは、2つの識別器のうちどれかが正解であるという意味である。一番理想的なのは $m \neq n$ ならば常にどれかが正解であるときなので、下限は $\bar{R}(f)/M$ である。
一番理想的ではないのが、すべての状況においてどの2つの識別器も間違えていること。これは $\bar{R}(f)$ と同じになってしまう。

つまり、できるだけ各モデルが違っていることが望ましい。

これを実現するための手法として、BaggingとBoostingが存在する。

Bagging

ランダムに訓練に使用するデータを選び出して、 $M$ 個のモデルを訓練する。モデル間で訓練に使用されるデータはお互いに排他的である必要はない。最後には、Votingで決定する。

Random Forestは、モデルを決定木(浅め)のものに限定するBaggingといえる。

AdaBoost

各モデル(Weak Classifier, Base Classifier) $f_m(\mathbf{x})$ に重みを与えて和をとり、理想的なStrong Classifierを作り出す手法。

F(\mathbf{x}) = \sum_{m = 1}^M \alpha_m f_m(\mathbf{x})

各Weak Classifierの違いをできるだけ大きくしたいには、以下の手法を用いる。 $m$ 個のWeak Classifierをすでに学習したとき、次の訓練を行うときに「今までの $m$ 個のWeak Classifierが間違えたサンプルの重みを大きくして」訓練を行う。つまり今までで間違えたサンプルの重みを大きくして、学習器に学ばせるインセンティブを大きくすることである。

二値分類のAdaBoostの実装例

M # Mイテレーションする
X, y # N個のサンプル
sample_w = np.full(N, 1.0 / N) # 重みは1/Nで初期化
classifier_w = np.zeros(M)
classifier # 長さMの配列だとする。

for m in range(M): 
	classfier[m] = train(X, y, sample_w)
	predictY = classifier[m](X)
	err = clacError(y, predictY, sample_w)
	
	# 今の識別器の重みは、errが大きいほど軽くする。
	classifier_w[m] = 1/0 / 2.0 * np.log((1 - err) / err)
	
	# サンプルの重みを調整する。
	for i in range(N): 
		# 各入力について、今の識別器で間違えたもの(classifier(X[i]) * y[i]で負になる)について、今の識別器の重みを乗じて、expの指数を正にして影響を大きくする。
		# 逆にあっているものは、今の識別器の重みを乗じて、expの指数は負になるので影響は小さくなる。
		sample_w[i] = sample_w[i] * np.exp( -classifier_w[i] * classifier[m](X[i]) * y[i])
	
# 出力
# xを予測
x
output = 0
for m in range(M): 
	output += (classifier_w[i] * classifier[i](x))

Self-trainingとCo-training

少量のラベルありと大量のラベルなしデータで学習を行う=Semi Supervised Learningという。

Self-training=Bootstrapping

まずラベルありサンプルでモデル $M$ を訓練する。
$M$ でラベルなしサンプルを予測してみて、そこで高い信頼度が与えられたラベルをpseudo labelとして、本来はラベルなしのサンプルの仮ラベルとして扱う。
仮ラベルと本当のラベル持ちのデータで再度モデルを訓練。2へ戻る。適当なところで切り上げる。

欠点としては、📄2020-Survey-Learning from positive and unlabeled data: a survey にもあるように、最初から間違えると一生響いて終わる。

Co-training

2つの異なる視点=viewを持つ識別器で互いに教えあう感じ。2つの視点 $V_1, V_2$ について見たサンプル $\mathbf{x}$ はそれぞれ $\mathbf{x}_1, \mathbf{x}_2$ である。仮定として、以下のものを置く。

条件独立性　2つの視点は独立である。 $Pr(\mathbf{x}_1, \mathbf{x}_2 | y) = Pr(\mathbf{x}_1 | y) Pr(\mathbf{x}_2 | y)$ が成り立つ。
冗長性　サンプルが十分に多いとき、 $V_1, V_2$ いずれの視点自身だけでも正確な分類器を訓練できる。

これらの仮定は現実的には難しいが、満たしたときに一番Co-trainingが有効である。以下のように学習を行う。

学習の疑似コード

N, X, y # ラベルつきはX, yであり、N個持つ。
M, U # ラベルなしはUであり、M個持つ。
T # Tはイテレーション数
K # Kは各イテレーションにラベル付けするUのサンプル数
P # 毎イテレーションにpseudo labelを付与してUから減らす数。2つの識別器でそれぞれP個とるので、毎イテレーションごとに2 * P減る。

f_1, f_2 # モデル

for t in range(T): 
	train(f_1, X, y) # f_1とf_2は異なる視点からTrainingしている前提である！
	train(f_2, X, y) # f_1とf_2は異なる視点からTrainingしている前提である！
	
	u = random_select(U, K) # UからK個ランダムに選ぶ。
	predictY = f_1(u)
	for p in range(P): 
		label = select_label(y) # 今あるラベルの分布の中から1つ選択する。各ラベルの割合の重みで
		trustful_u = select_trustful(u, predictY) # labelについて最も信頼度が高いuのサンプルにpseudo labelを付与
		X = add_element(X, trustful_u)
	# 同様にf_2についてもやる。

つまり、先ほどのBootstrappingを2つの識別器で同時にやっている。お互いに関係ない視点ならば2倍速いが、完全に同じ視点ならば1つの識別器でやることと全く同じになる。

Multi-task Learning

一定の関連を持つタスクの間では、何かしらの共同の知識を使っていると考えられる。ここで、うまく共同の知識をまず訓練し、次にその共同の知識を使って各自のタスクへの特化を行うことができる。うまくいくと訓練の手間が省ける。

いかに情報を渡しているのかはいろいろなやり方がある。

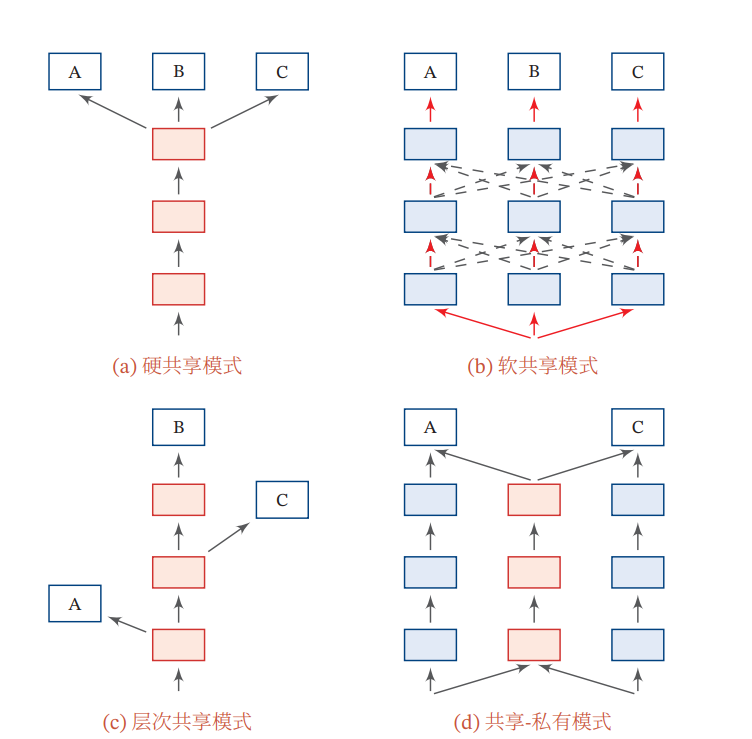
(a) Hard Parameter Sharing 明確に共有する特徴量を選び、それを共有する。
(b) Soft Parameter Sharing 隠れ状態を少し使う、Attentionを使って隠れ状態から情報を選ぶ、損失関数で訓練方向に意図させるなどをして、明示的な共有する特徴量を持たないならも共有するやり方。
(c) 複数の層(浅い、深い)でそれぞれタスクの需要に応じて抽出する。
(d) Public-Private 赤はPublic、青はPrivateのようにする。必ずしも赤→青という流れではなく、層が入り乱れてもOK。

詳細はここのメモがいい。 🚫 Post not found

Transfer Learning(迁移学习)

訓練サンプルとテストサンプルの分布が異なるとき、うまくDomain Shiftに対処する必要がある。

入力 $\mathcal{X} = \mathbb{R}^D$ で、出力が $\mathcal{Y}$ であり、確率分布 $Pr(\mathbf{x}, y)$ を持つ。ドメインは $\mathcal{D} = (\mathcal{X, Y}, Pr(\mathbf{x}, y))$ から成る。

Transfer Learningは、Source Domainで大量に学習した知識を使って、Target Domainでの学習に転用するものである。

Transfer Learningの中でも、Inductive Transfer Learning=归纳学习とTransductive Transfer Learning=转导学习がある。

前者は訓練サンプルとそのラベルを知るという条件で学習を行う。
後者は訓練サンプルとそのラベルのみならず、テストサンプル(ラベルは不明)もそれらの関係性(距離など)も学習に使ってよい。
- 別のテストサンプルに対してこれは適用できない。なぜなら、学習に使ったテストサンプルのドメインと、新たに得たテストサンプルのドメインが異なるから

参考: https://blog.csdn.net/qq_40210586/article/details/118544771

Inductive Transfer Learning

Source DomainにはUnlabaledしかない場合は、Auto-EncoderやDensity EstimationなどのUnsupervised Learningを行い、それをTarget Domainへの転移を行う。言語モデルでは非常に有効なテクニックである(大量にあるドキュメントのラベル付けは大変)。

Source DomainにLabeledのサンプルが大量にある場合、Source Domainで訓練し、そのパラメタをそのままTarget Domainに援用すればよい。(Multi-task Learningと似ているね)。

DNNに対してInductive Transfer Learningを行う場合、浅い層の特徴量、深い層の特徴量それぞれを用途によって使い分けるのが望ましい。

これを用いると、学習が早く、汎化性能もよいというメリットがある。

具体的な実装法は2つある。1つはSource Domainで訓練したものの中間層表現や出力を入力として、追加で数層設けてそれで訓練を行わせる手法。ここでは、追加した層だけパラメタは学習させ、もともとある層のパラメタの学習は凍結させる。

Fine-tuning

Fine-tuningはInductive Transfer Learningの1つの変種。同じようにネットワークを追加するが、もともとある層のパラメタの学習「も」行う。

Transductive Transfer Learning

Inductiveと異なり、テストドメインのサンプルはラベルは不明ながらも、分布自体を予測できるという前提

典型的なTransductive Transfer LearningのタスクはDomain Adaptation。同じ $\mathcal{X, Y}$ を持つが、分布が異なる場合である。つまり、 $Pr_S(\mathbf{x}, y) \neq Pr_T(\mathbf{x}, y)$ である。

Pr(\mathbf{x}, y) = Pr(\mathbf{x}|y) Pr(y) = Pr(y | \mathbf{x}) Pr(\mathbf{x})

ベイズの公式で上が成り立つことから、分布が異なる理由は以下の3つに分けられる。

共変量シフト(Covariate Shift)　SourceとTargetの入力分布が異なる $Pr_S(\mathbf{x}) \neq Pr_T(\mathbf{x})$ 場合。ただし、ラベルの事後分布は同じである $Pr_S(y|\mathbf{x}) = Pr_T(y|\mathbf{x})$ 場合。
1. 例)ソース: 夏ターゲット: 冬　タスクは気温からアイスの売り上げを予測する。
  1. 夏と冬は入力 $\mathbf{x}$ =気温の分布が異なるが、しかし気温 $\mathbf{x}$ と売り上げ $y$ の関係性は一定という考え。
2. ラベル付けの基準は一定だが、データは違う。
3. 今主流の問題設定
概念シフト(Concept Shift)　SourceとTargetの入力分布は同じである $Pr_S(\mathbf{x}) = Pr_T(\mathbf{x})$ 。しかし、ラベルの事後分布が異なる $Pr_S(y|\mathbf{x}) \neq Pr_T(y|\mathbf{x})$ 場合。
1. 例)ソースもターゲットも: 文章の入力　文章から感情の分析をする。
  1. 同じ文章 $\mathbf{x}$ であったとしても、時代によって意味が異なってくる=文章 $\mathbf{x}$ を受けてのラベル $y$ の事後分布が異なる。
2. データは一定だが、ラベル付けの基準が違う。
事前情報シフト(Prior Shift)　ラベルの事前情報分布が異なる $Pr_S(y) \neq Pr_T(y)$ 場合。しかし、ラベルごとの入力分布は同じ $Pr_S(\mathbf{x}|y) = Pr_T(\mathbf{x}|y)$ である。
1. 季節ごとに病気= $\mathbf{y}$ の分布が異なる。しかし、症状 $\mathbf{x}$ から病気への診断 $\mathbf{y}$ の確率は常に一定である。
2. ラベル付けの基準は一定だが、ラベルの分布が違う。

Covariance Shiftについて

Covariance Shiftを数式で見てみる。以下のように、密度比の変換が重要。

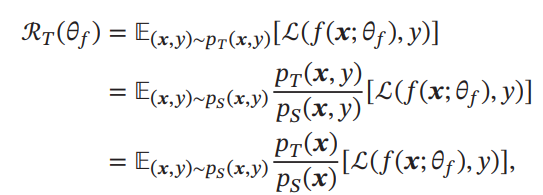
もし、写像 $g : \mathcal{X} \to \mathbb{R}^d$ があり、 $Pr_S(g(\mathbf{x} | \theta_g)) = Pr_T(g(\mathbf{x}|\theta_g))$ と、写像 $g$ で変換すると同じ入力の分布を得ることができるのならば、損失関数は以下のように書き直せる。

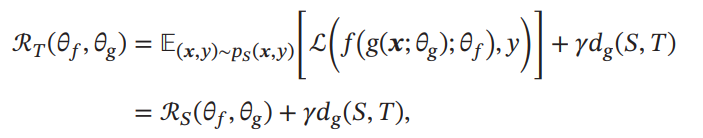
第1講はSource Domain上の損失であり、 $\gamma$ のハイパーパラメタに制御された第二項はSourceとTargetの分布の距離である。

学習では $\theta_f, \theta_g$ を学習して、Source Domainでの損失を最小化しつつも、できるだけDomainに依存しない特徴を抽出させたい。実現方法としては、Multi-task Learningにもあったように敵対的な識別器を用意して、この特徴量はDomain依存で判定できるか？を訓練させて識別できないものをDomainに依存しない特徴量として扱っている。

Continuous Learning(Lifelong Learning)

既存の学習した分野をもとに新たな知識を捉えていく人間は、機械学習のようにあるタスクについて学習し終えた後他のタスクを学習させると元のタスクの知識が忘れることはない。

Conductive Transfer Learningと似ているが、あちらは最終的なタスクの性能だけに着目していた。ここでは、途中の学習による知識の累積にも注意を払う。

これを実現するためには、Catastrophic Forgettingという重要なものを忘れてしまうのをなんとしても防がねばならない。ただ、解決自体は希望的である。現在のDNNはパラメタ基本的に過多であり、タスクAの高い性能を実現するようなパラメタの組は多数存在する。その中で、タスクBの性能を上げるときにタスクAの性能を損なわないものを見つければよい。

解決法の1つとして、Elastic Weight Consolidationである。

Elastic Weight Consolidation

参考: https://qiita.com/yu4u/items/8b1e4f1c04460b89cac2

タスク $T_A, T_B$ がそれぞれサンプル集合 $D_A, D_B$ を持つとする。 $D = D_A \cup D_B$ 。ここで、2つのタスクはそれぞれ独立に生成されたと仮定する(独立ではない場合はMulti-Task Learningで独立まで共同な特徴量を学べそう)

\log Pr(\theta | D) = \log Pr(D | \theta) + \log Pr(\theta) - \log Pr(D)

ベイズの定理により成り立つ上式を以下のように書き換えられる。このパラメタの事後確率を最大化したい。

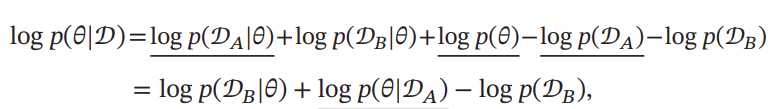
下線部はベイズの定理により下式の二項目へとまとめられる。ここで、 $-\log Pr(D_B)$ は定数なので関係ない。

$T_A$ を学習した後のパラメタの分布 $Pr(\theta | D_A)$ である。確かに $T_A$ について学習して学習器を得たが、今のパラメタとなった時の事後確率自体を計算するのは難しい。

ここで、フィッシャー情報行列による近似を考える。

参考: https://masamunetogetoge.com/fisher
$Pr(\mathbf{x}|\theta)$ のパラメタ $\theta$ についての情報量を測定する指標。パラメタ $\theta$ の分布への影響は、gradientの大きさと考えられる(動いたらどれほど影響するか)。(パラメタ $\theta$ は太文字ではないが、複数のパラメタであるので、gradをとるとvectorになる)

s(\theta) = \nabla_\theta \log Pr(\mathbf{x} | \theta)

このように、対数尤度のgradをスコア関数とする。なお、このスコア関数の期待値 $\mathbb{E}[s(\theta)] = 0$ である。そして、フィッシャー情報行列は以下のように定義される。つまり共分散行列である。

F(\theta) = \mathbb{E}[s(\theta) s(\theta) ^ T]

共分散行列なので、非対角成分はパラメタ間の相関の強さ(増えたら一緒に増えるか)をあらわす。対角成分が大きいほどそのパラメタの分散が小さく、信頼できる値だということ。

意味としては対数尤度の曲率であり、対角成分で曲率が高いほど急激に曲がっている=パラメタが鋭敏=推定が十分に正しい、という意味。

どのように使うか

$T_A$ についての事後分布を $Pr(\theta|D_A) = \mathcal{N}(\theta_A, F^{-1})$ で近似できるとする(フィッシャー情報行列の対角成分だけ使って分散逆行列を構築できる)。すると、 $T_A$ を学習するときの損失関数は、本来のものに加えてフィッシャー情報量をも使う。 $\theta_{A,i}^*$ は $T_A$ で学習したときのパラメタ。

L(\theta) = L_B(\theta) + \sum_{i=1}^N \frac{\lambda}{2} F(\theta)_{i,i} (\theta_i - \theta_{A, i} ^ *)^2

対角成分が高い=曲率高く少し動かすだけで変わる=確実性が高いパラメタほど、今のパラメタと $T_A$ で訓練したパラメタに差がつかないようにしたい。

Meta-Learning(元学习)

参考: https://qiita.com/25226153/items/bf37c8ce5f128897e9e7

複数の作業を通じて学習のテクニックやコツを理解し、未知の作業に応用したい。モデル自体を入力として学習を行っていく。目標は多数のモデルから、1つの通用する流れを作りたいということ。基本的に、学習率を何倍にすると早く学習できるか？を学んでいく。

Meta Learningの手法として2つあり、optimizerベースの学習とモデルに依存しないMeta-Learningがある。

Optimizerベースの学習

Meta Learningによって、タスクの学習の学習率による進む度合いを決めていく。 $g$ という進み度合いを訓練することによって、

\theta_{t+1} = \theta_t + g_t(\nabla L(\theta_t); \phi)

$g$ の実現にはいろいろなやり方があるが、値を保存していくLSTMでgradientを覚えていたりすることができる。各パラメタごとにLSTMをよういするのは非現実なので、1つのLSTMでパラメタのgradientを覚えるほうがいい。

モデルに依存しないMeta-Learning

すべてのタスクが1つの空間に所属しているとする。この時普遍的な勾配降下の方法を学ぶことに意義がある。ある学習したモデル $f_\theta$ について、 $\mathcal{L_{T_m}}$ を学習することで新たなタスクの降下度合いを学ぶことができる。

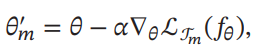
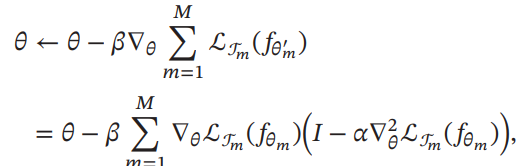
このように更新を行う。二回微分を求める必要があるが、一回微分から近似的に得られるものであっても、比較的に良い性能を得ることができるらしい。

上の $\alpha$ が小さいときは、マルチタスク学習の最適化のようになる(実質的に複数のタスクについてそれぞれの学習率を調節しているだけ)。