中国の有名な機械学習の本の勉強ノート。自分がわからなかったところだけなので飛び飛びだろう。
今までのネットワークでは以前の入力などに依存しない、デジタル回路で言うと組み合わせ回路であった。しかし、現実的には以前の入力は重要な影響を及ぼすのが普通であり、それが記憶という形でどこかしらで残っている。デジタル回路で言うと順序回路。これをNNで実現させたい。
ネットワークに記憶力を持たせるには
Time Delay NN
出力層以外の層に、直近数回のニューロンの出力値を記憶しておく。昔ながらの方法だが、今は性能不足である。
外部入力がある非線形自己回帰モデル
自己回帰モデルは時系列データの予測でよく使用されるモデル。はノイズ。
Recurrent Neural Network(RNN)
隠れ層について、時刻における状態をだとおく。すると、以下のように過去の隠れ層の状態と入力によって、今の隠れ層の状態を作り出すというモデル。
Simple Recurrent Neural Network(SRN)
1つの隠れ層だけを持つ、一番簡単なRNNの模型。時刻において、入力は、出力は、中間状態は。入力層の重みは、以前の中間状態に対する重みは、全体のバイアスはだとする。この時、DNNは以下のように更新される。
RNNには記憶能力が導入できた。これによって、チューリング完全であるとなり、理論上はチューリングマシンで表現できる関数の全てを表現できるようになった。
機械学習における応用
Sequentialな入力による最終的な分類
上の関数を、ロジスティック関数や他のDNNなどで予測ラベルに落とし込む。最後のものをとっても良いし、で平均をとってもいい。
Sequentialな入力による各段階の分類
どうようにロジスティック関数や他のDNNなどで予測ラベルに落とし込むが、は時刻における予測結果を表すという意味。
Encoder-Decoderモデル(异步的序列到序列模式)
長さの入力から、長さの出力を出すもの。
具体的には以下のようになる。
- 入力されるときは、によって隠れ状態を生成する。
- 入力が終わり(EOS)、によって、前回の自分の出力のと、前回の隠れ状態を入力として、今の出力をつくる。
- 前回の自分の出力を入れるので、自己回帰モデルともいう。
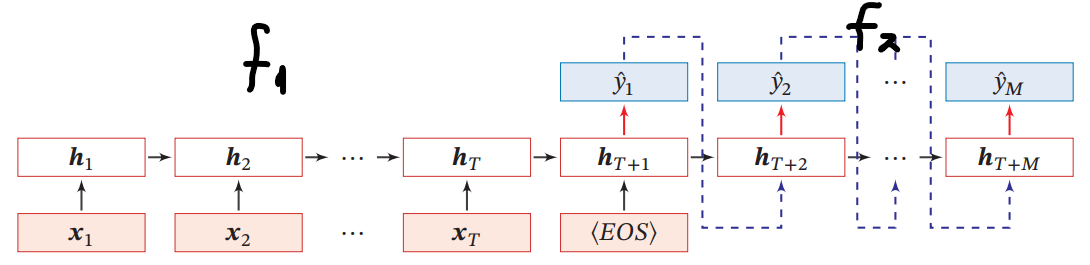
RNNにおけるパラメタの学習
RNNは長さの入力があるので、合計個の出力のが存在する。なので、損失関数はだとすると、合計で個定義できる。
このすべての損失について、全体的な損失を作る。クロスエントロピー損失ならば、加算をすればよい。となる。
これで、隠れ状態の重みのを学習すると考える。
Back Propagation Through Time(BPTT)
微分したときの傾きは、
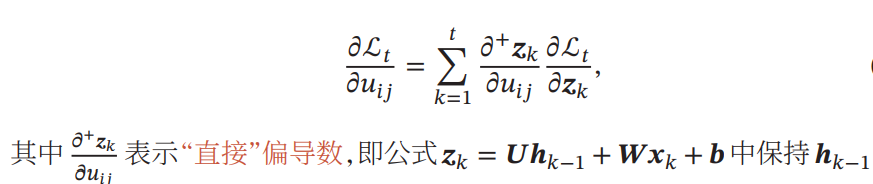
計算を進めると、以下のようになる。
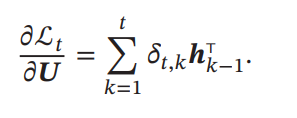
このように計算するとき、通常通りの順伝搬を行ってから、逆伝搬を行うことになる。微分を計算するとき、出力のカテゴリ数に依存しているため計算量自体は少ない(入力より出力の方が次元が少ないのが一般的)が、順伝搬を終わらせての逆伝搬となるので、すべてを記憶しなければならず、空間計算量の要求が非常に高い。
Real Time Recurrent Learning(RTRL)

一気に最後までIterationせずに、途中までその都度都度まで計算することもできる。具体的には、各ステップごとにgradientが求まるので、そのステップ時点で勾配降下を行うということになる。
正確にはBPTTとは異なるものを導くが、こちらはこちらでメリットを持つ。底が見えないもの、例えばオンライン学習や無限の長さの学習ではこの手法しかない。
Long Rangeにおける情報の消失
RNNは昔の入力をずっと理論上は伝播させることができるが、入力の長さが大きくなるにつれて、消えてしまう。について以下のように展開できる。
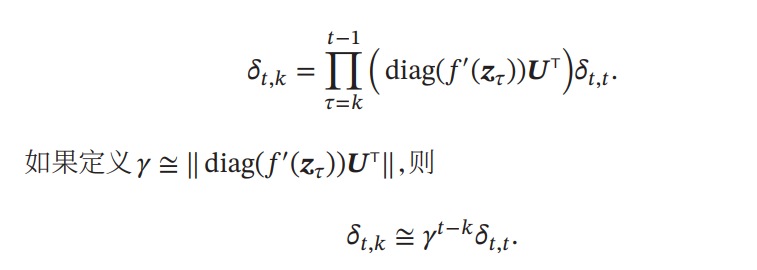
ここで、ならば、逆伝搬の計算を行う時に長さだけ指数的に拡大されて、非常に大きいgradientになる。これは、勾配爆発問題、Gradient Exploding Problemと呼ばれている。
逆に、ならば、指数的に縮小されてgradientが非常に小さくほぼ0になる。これは、勾配消失問題、Vanishing Gradient Problemという。(DNNでも起きていた問題)
理想的にであるべき。だが計算の綾で無理だろうから、やはりきつい。結果として、素のRNNでは長い依存関係を捉えることができないということになる。
RNNの実装例
PyTorchで実装してみた。簡単な時系列データの予測もしてみた。PyTorchのRNNやLSTMは、(seq_len, batch, input_size)の順にデータの次元が決まっている。参考: https://yonesuke0716.hatenablog.com/entry/2021/01/09/145500
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
# RNNのモデルの本体はここ。
class RNNHardCell(nn.Module):
def __init__(self, n_input:int, n_hidden:int, state=None) -> None:
super(RNNHardCell, self).__init__()
self.n_input = n_input # 入力の特徴量の数
self.n_hidden = n_hidden # 隠れ層の数
self.in_h = nn.Linear(self.n_input, self.n_hidden, bias=True) # 入力x_iに乗じる重み
self.h_h = nn.Linear(self.n_hidden, self.n_hidden, bias=True) # 1つ前の隠れ状態h_{i-1}に乗じる重み
self.state = state # 今持っている隠れ状態h
self.register_parameter() # パラメタの初期化
# パラメタの初期化。伝統的に標準偏差は1/sqrt(n)でやっている。
def register_parameter(self) -> None:
stdv = 1.0 / math.sqrt(self.n_hidden)
for weight in self.parameters():
nn.init.uniform_(weight, -stdv, stdv)
def forward(self, x, state=None):
# ここでは、活性化関数はhardtanhにしている。
self.state = state
if self.state is None:
self.state = F.hardtanh(self.in_h(x))
else:
self.state = F.hardtanh(self.in_h(x) + self.h_h(self.state))
return self.state
# モデルをどのように、再帰的にやってRNNを実現させるかを記述する。
class RNNModel(nn.Module):
def __init__(self, n_input, n_hidden, n_output, num_layers=1):
super(RNNModel, self).__init__()
self.rnn = RNNHardCell(n_input, n_hidden) # 先ほど定義したRNN
self.out = nn.Linear(n_hidden, n_output, bias=False) # 出力する前の全結合層
self.num_layers = num_layers # 複数のRNNをつなげて予測モデルを作れるということ。
def forward(self, xs, state=None):
state = None
h_seq = []
for x in xs: # ループを使って各時間順にのデータを入れていく。
x = torch.from_numpy(np.asarray(x)).float()
x = x.unsqueeze(0) # batch学習扱いなので
for _ in range(self.num_layers):
state = self.rnn(x, state) # このようにstateを更新していくことでRNNを実現する。
h_seq.append(state)
h_seq = torch.stack(h_seq)
ys = self.out(h_seq)
ys = torch.transpose(ys, 0, 1)
return ys改善の試み
理想的にとするのは不可能だし、毎回無理やり1に較正しても表現力が落ちるなどする問題が起きる。
勾配爆発は、
- パラメタが大きくなり過ぎないように、L1やL2正則化を行う。
- 勾配が一定値を超えた時、無理やり上限をに制限する。
この2つを使うことで、勾配爆発はの勾配消失の問題に一般化することができる。
勾配消失については以下のように対策している。ここでのは隠れ状態を入力して次の隠れ層を出力するための関数示している。
ここで、次のようなを代わりに学習する、ResNetのような設計方法を考える。
この時、との比率は1対1であり、RTRLで学習するときは勾配消失や爆発を和らげられる。
だが、まだ解決が完全にできるわけでもないうえ、どんどんが入ることによって、隠れ状態のが表現できる情報の量に限りがあって溢れてしまう。どうしても情報が不完全なものになってしまうという欠点がある。
Long Short Term Memory-network(LSTM)
以下の記事を参考にした。https://blog.csdn.net/v_JULY_v/article/details/89894058
すべてを覚える必要はない。長期記憶と短期記憶に分ける。短期記憶は、今まで通りの隠れ状態であり、別途長期記憶というを設定する。
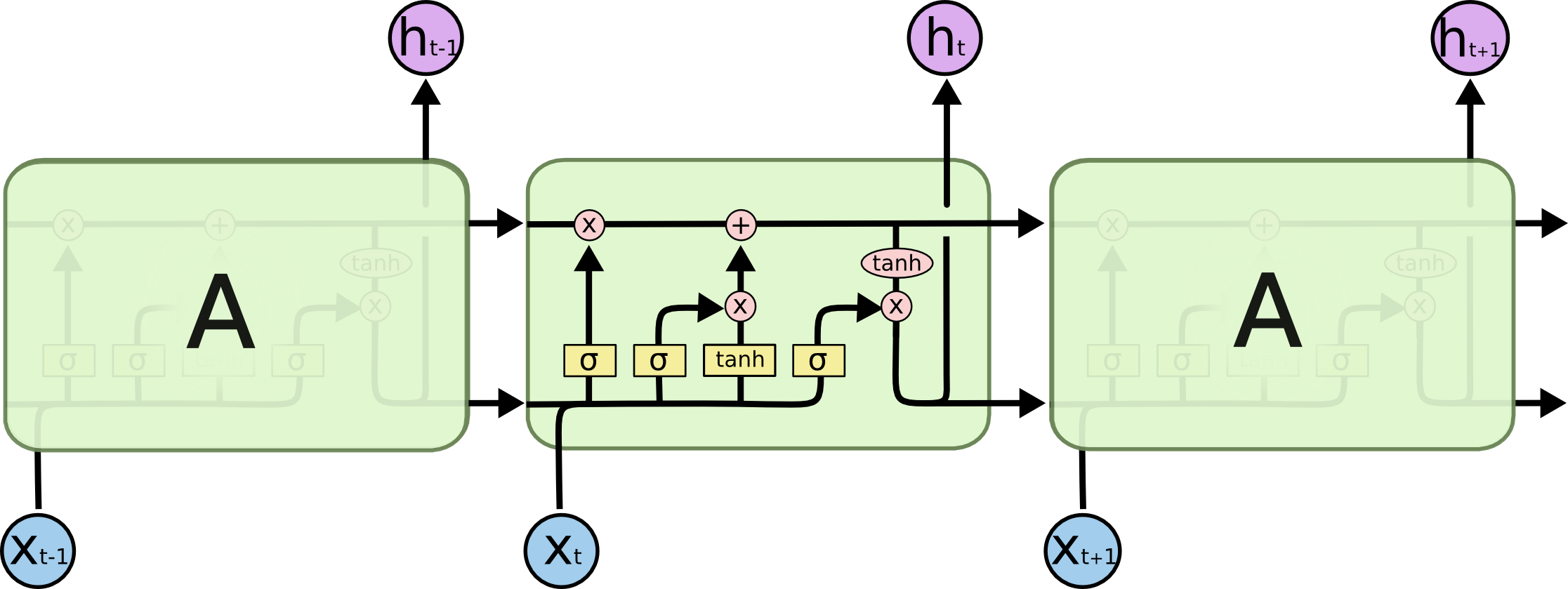
各矢印の意味は以下の通り

一番上のは長期記憶であり、下は短期記憶である。左から順に説明する。
- まず、短期記憶と入力を結合したベクトルを考える。
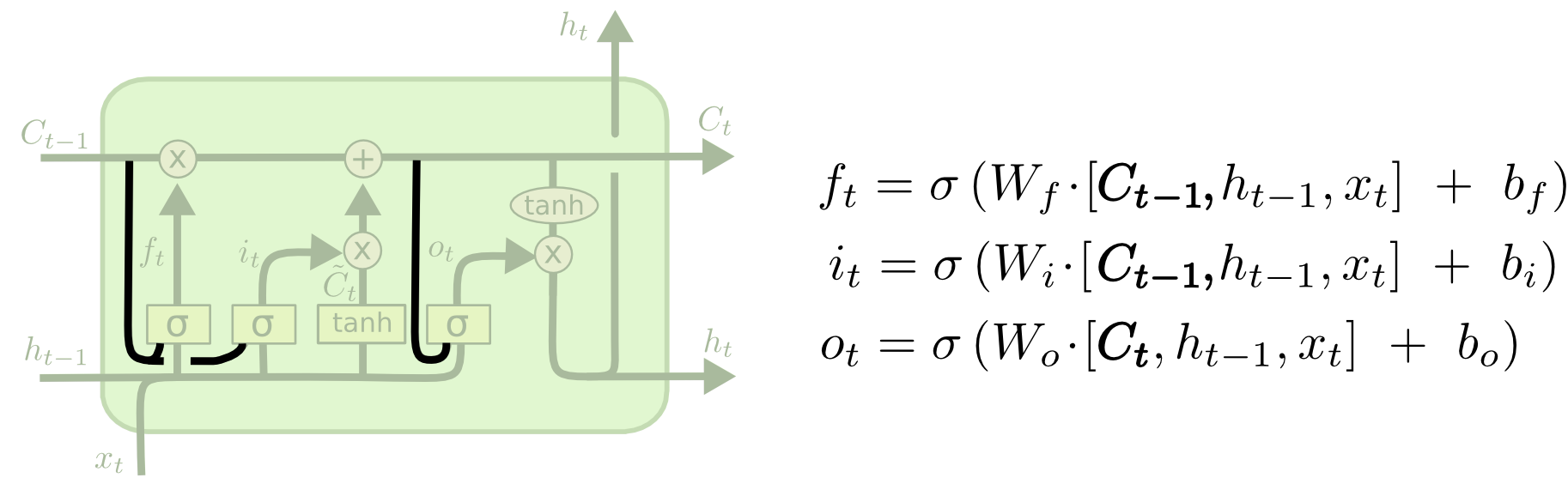
- まずは、忘却ゲート。
- sigmoid関数を用いた層で、と各次元ごとにsigmoid関数を適用することで、0から1までの成分からなるベクトルを作る。
- で更新する。これによって、長期記憶の各次元の成分を一定の割合消すことができ、「忘却」させることができる。
- 次は、入力ゲート。
- 同様にsigmoid関数を用いた層で、忘却ゲートの時と同じようにでベクトルを生成する。
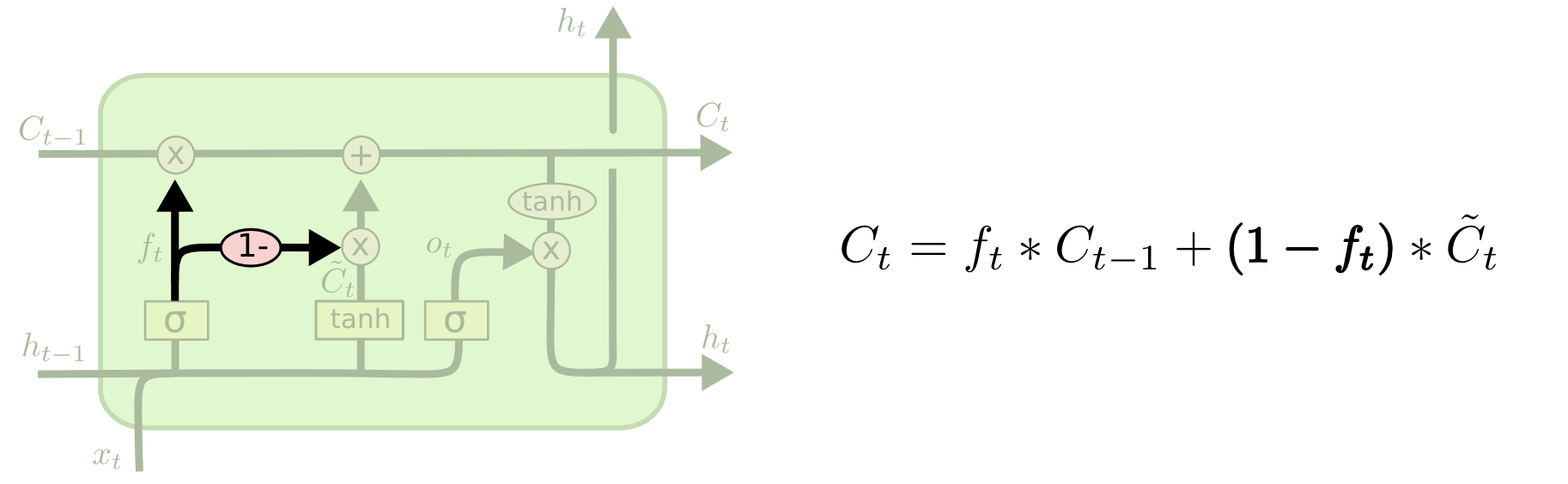
- 次は、長期記憶のアップデートしていく。今回の長期記憶への追加情報となるベクトルをつくる。。
- 。このように追加していく。
- 忘却ゲートと入力ゲートの2つ長期記憶の更新がなされる。式をまとめて書くと以下の通り。
- 最後に、出力ゲート。短期記憶はそのまま出力となるという設計。
- 今までと同様にsigmoid関数を用いた層で、忘却ゲートの時と同じようにでベクトルを生成する。
- 更新した長期記憶を用いて、tanh関数によってへ変換する。それを先ほど生成したとアダマール積を取る事で、短期記憶を更新する。長期記憶を符号つきの値ん位落とし込んで、短期記憶を更新する。
これらの機序が、太初のLSTMというものである。
実装例
LSTMの亜種たち
様々な亜種が存在しており、簡単に紹介する。
peephole連結
以下のように、3つのゲートすべて(忘却ゲートと入力ゲートと出力ゲート)の計算に、パラメタとして長期記憶も使う。つまり、NNの層に入れるのは、長期記憶、短期記憶、今の入力すべてを結合したベクトル。
coupled連結
今までは忘却ゲートと入力ゲートは別々に決定されたが、入力ゲートの値を以下のように固定する。
Gated Recurrent Unit(GRU)
長期記憶と短期記憶を1つのものに混ぜ込んで、忘却ゲートと入力ゲートを1つにまとめた。

- peepholeのように、実質的に長期記憶、短期記憶、入力のすべてを使ってに作る。
- はcoupled連結のように、(長期記憶に対して)忘却するものと新たに記憶するものを相補的なゲートのベクトルにする。
- はと同じようなモデルで作られるが、これはを事前に(あるゲートを通してだが)コピーをしておく意味である。それを使って、入力を結合して次の記憶する情報のベースたるを作っている。
結局どの亜種の性能がいいの?
本質的には同じくらい良いです。
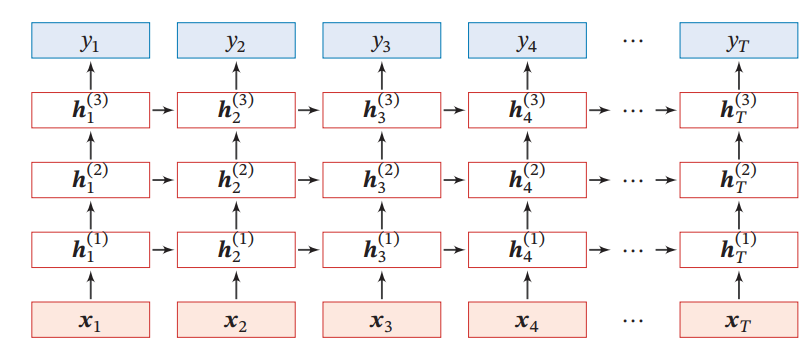
Deep Recurrent Network
Stacked Recurrent Neural Network(SRNN)
RNNについて、隠れ状態を増やして、の隠れ状態との1つ下の隠れ状態から入力を得ていく設計。
Bidirectional Recurrent Neural Network(Bi-RNN)
自然言語処理では、単語は前の単語たちのみに依存することはなく、後ろの単語にも依存する。これを実現する一例として、以下のような
- まずは時間順に伝搬する。これはとなる。
- 次は逆時間順に伝搬する。これはとなる。
- 2つの隠れ状態を結合して新たなベクトルを作る。
- ここまでは同じ時間での話。
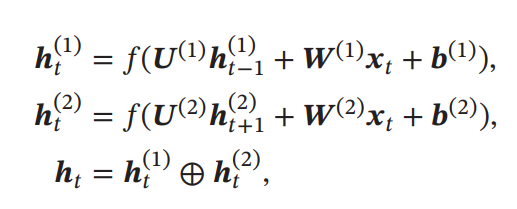
Graph Neural Networkへの拡張
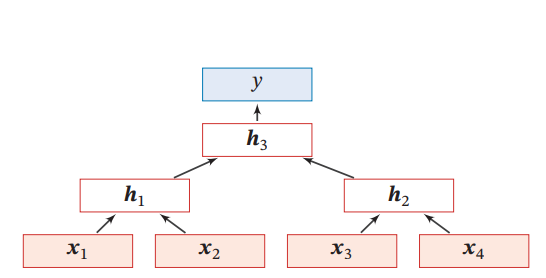
Recursive Neural Network(RecNN)
DAGの上でRNNを伝搬させること。先ほどのSRNNは隠れ状態はきれいな1本の流れであったが、それがDAGに代わる場合。以下の場合はちょうど二分木になっている場合。
Graph Neural Network(GNN)
グラフ上でのすべての頂点について、時刻のは、1つ前のの頂点と、頂点に隣接してる頂点とその辺の特徴を入力する。そして、すべての隣接する頂点について、非線形層を通した後に合算する。
そこからとの頂点における情報を統合して、最終的に新たなを作る。
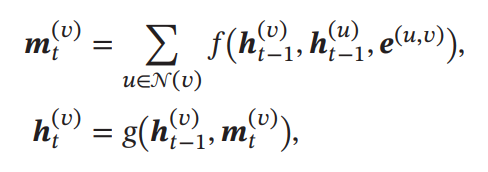
演習してみた
RNN
PyTorchにあるRNNを使って、簡単な時系列データのパターン予測をしてみた。
