NNDL 第4章 NN(ニューラルネットワーク)

中国の有名な機械学習の本の勉強ノート。自分がわからなかったところだけなので飛び飛びだろう。

https://nndl.github.io/

ニューロン Sigmoid型活性化関数 ReLU型活性化関数 Swish型活性化関数 GELU型活性化関数 Maxout型活性化関数ネットワーク構造 Forwarding Neural Network 誤差逆伝播法最適化するにあたって勾配消失問題 PyTorchでの実装例

ニューロン

入力 $\mathbf{x} \in \mathbb{R}^D$ に重み $\mathbf{w} \in \mathbb{R}^D$ を乗じて、そこにバイアスの $b$ を足した後に、活性化関数(Activation Function)の $f$ を乗じたものがニューロンであり、NNの最も基本的な構成要素。

a = f(\mathbf{x} ^ T \mathbf{w} + b)

$f$ が01損失であれば、パーセプトロンである。

Sigmoid型活性化関数

活性化関数としてよく使われうのが、以下のようなものである。

Logistic関数。これは実数を $(0, 1)$ に制限するともいえる。

\sigma(x)=\frac{1}{1 + \exp(-x)}

Tanh関数。これは実数を $(-1, 1)$ に制限するともいえる。

\tanh (x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)} = 2 \sigma (2x)- 1

これらはすべてSigmoid型の活性化関数。

Logistic関数のように、出力する値の中心が1/2であるので、何層も層を重ねるとそれぞれが出力する値はだんだんと1に近くなる。このとき、Sigmoid関数の傾きは非常に小さくなるので、勾配降下法による最適化が遅くなる、欠点をもつ。

いずれも指数関数を計算に用いることで、計算コストが重いという欠点を持つ。代替案として、マクローリン展開で一次式で近似するということができる。微分不可能な点が生じてしまうが。

Hard-Logistic関数。

\max(\min(x/4 + 1/2, 1), 0)

Hard-Tanh関数。

\max(\min(x, 1), -1)

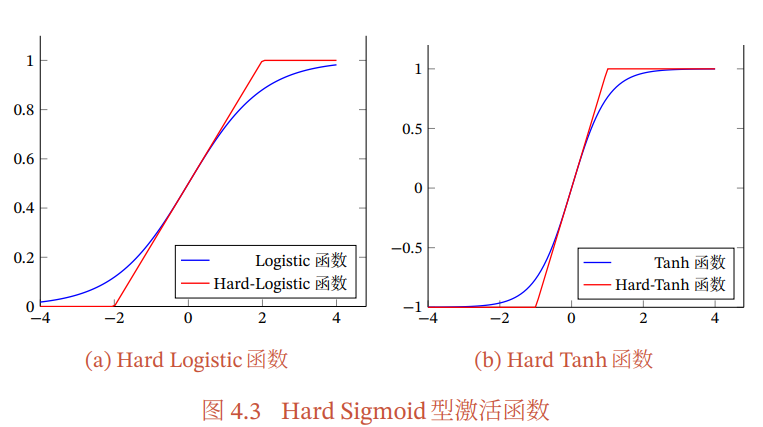
ReLU型活性化関数

興奮度合いが1を超えて上がる、少数のニューロンをアクティブにするという生物学的な合理性を持つReLU関数。

\max(0, x)

傾きが小さすぎて勾配消失しかねない問題をある程度解消できる。

ただ、Sigmoidと同様に、ReLU関数も出力の中心が0ではなく、層を重ねるごとに勾配降下法での最適化の効率が悪くなる。また、パラメタのgradientが大きい結果、がっつり更新してその結果、他のどんな入力が来てもReLU関数の引数には負しか与えられず、永久にそのニューロンが使えなくなる=Dying ReLU Problemが起きてしまう。

これの改善としての提案はLeakly-ReLU関数。

\max(0, x)+\gamma \min(0, x)

$\gamma$ は1より非常に小さいながら正のパラメタである。これによって、たとえReLUでDyingしたとしても、小さいながらも傾きを持つことによって、勾配降下法でReLUの入力を正に引き戻すことができる。

他にも $\gamma$ を各々のニューロンごと、複数のニューロンごとで共有して(Leaklyのように決まり切った値ではなければ全部同じでも、それぞれ別々でも構わない)、それも学習する変数としたパラメトリックReLUもある。

他にも、ReLUのような形を持つものは以下のものがある。

Exponential Linear Unit(ELU)関数。

\max(0, x) + \min(0, \gamma(\exp(x) - 1))

Softplus関数。

\log(1 + e^x)

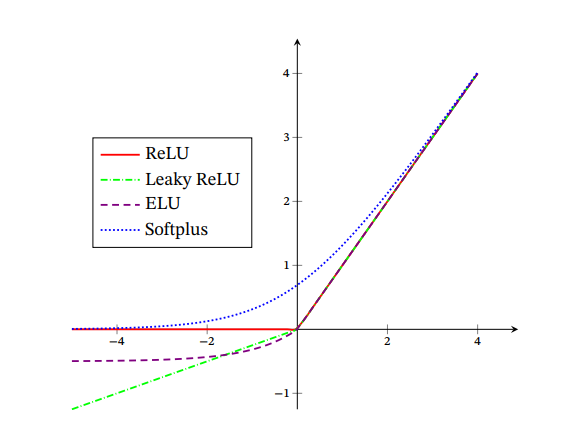
Swish型活性化関数

Self-Gatedであると言われている。GatedというのはReLUみたいに、明確にON、OFFを指し示す値(01がふつう)ができてるということ。

\sigma(x) = \frac{1}{1+e^{-x}} \\ x\sigma(\beta x)

$\beta$ はハイパーパラメタでも学習させるパラメタでもよい。

GELU型活性化関数

Gaussian Error Linear Unit。

P(X \leq x) \sim \mathcal{N}(\mu, \sigma^2) \\ x P(X \leq x)

これはSwish関数に似ている。

Maxout型活性化関数

ReLUのような曲がり角を複数個許容し、0でなくてもよくしたもの。凸の折れ線グラフって感じ。

\forall i, z_i = \mathbf{w}i ^ T \mathbf{x} + b_i \\ \max _{i} (z_i)

ネットワーク構造

一般的に使われるネットワーク構造は以下の3つ。

Forwarding Neural Network(前馈网络)　普通に我々が知っているネットワーク。DAGになっていて、各層の構造を持つ形。表現も関数の合成写像であると言える。回路でいうとCombinational Circuit。
Memorization Neural Network(记忆网络)　RNNなどの状態の記憶ができるネットワーク。回路でいうと、Sequential Circuit。
Graph Neural Network(图网络)　DAGという制約も消えた、グラフでのネットワーク。

Forwarding Neural Network

第0層目は入力で入力層、最後は出力層、真ん中はすべて隠れ層。層を深くすることで、Deep Neural Network=DNNとなる。一般的には出力層はsoftmaxであり、いろんな値を確率に較正する。

NNの特性として、niversal Approximation Theorem(通用近似定理)がある。これは、いかなる関数であっても、適切な活性化関数と有限の数のニューロンによって表現することができるというもの。つまり、NNの表現力は理論上無限大。

実際では、うまく与えられた特徴量から、よりよい特徴量 $\phi(\mathbf{x})$ を得ると訓練の効果が良くなる。

解決法は色々あるが、簡単で有効な手法はReLUのようにそもそも勾配が0か1かしかないものを使うことですね。

PyTorchでの実装例

全結合層によるNNである。

実装例。

import torch
import torch.nn as nn

# ネットワークの定義
network = nn.Sequential(
    nn.Linear(784, 128),  # 入力層から隠れ層への全結合層 (例: 784はMNISTの画像サイズ28x28を平坦化したもの)
    nn.ReLU(),            # 活性化関数ReLU
    nn.Linear(128, 64),   # 隠れ層からさらに別の隠れ層への全結合層
    nn.ReLU(),            # 活性化関数ReLU
    nn.Linear(64, 10)     # 最終層から出力層への全結合層 (例: 10はクラス数)
    # 出力層に活性化関数が必要な場合はここに追加します (例: 分類問題の場合は nn.LogSoftmax(dim=1) など)
)

# ネットワークの概要を表示
print(network)