中国の有名な機械学習の本の勉強ノート。自分がわからなかったところだけなので飛び飛びだろう。
再度いうが、理論上DNNとRNNは非常に強力である。DNNは任意の関数を近似できるし、RNNはチューリング完全である。しかし、最適化のやり方や処理能力(そんなに大きいネットワークは作れない)の制約上、CNNなどの賢いアーキテクチャを事前に人間考えて訓練させないとなかなか性能出ないということがわかった。
ネットワーク内で保存できる情報量はNetwork Capacityと言う。一般的には、RNNの保存できる情報量はニューロンの数とネットワークの複雑度に比例する。
しかし、これは人間の脳も同じである。わずか数秒しか覚えられない脳は、RNNでいう記憶消失問題そのものを抱えている。しかし、人間には注意力=Attentionと、長期記憶を持つ。
Attentionとは
大量の情報がある中で集中的にみる分野を選び出すことをAttentionという。以下の2種類ある。
- Focus Attention 意識的に○○に集中すること
- Saliency-Based Attention 無意識に、周りとすごく違うものに注目すること
CNNのMaxPoolingやRNNのGate制度は、Saliency-Based Attention(意識的に最大)を行っているといえる。
入力がと与えられるとき、重要な情報だけに注目したい=一部の情報をそぎ落としたい。
ここで、Query Vectorというを導入し、これに従って番目のVectorが選ばれる確率を定義したい。
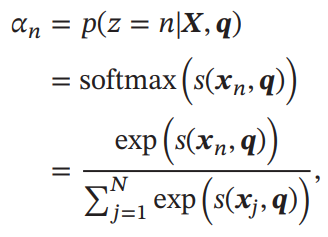
離散的ではなく連続的に扱いたいので、softmaxを噛ませてCalibrationしている。そして、とは、サンプルがQuery Vectorの下でどれほど選ばれるべきかのスコアを出力するスコア関数。スコア関数は以下の数通りありえる。
| スコア関数のモデル名 | 形 | 学習するパラメタ |
| 加算モデル | ||
| 内積モデル | ||
| スケールつき内積モデル | ここではの次元 | |
| 二次形式モデル |
理論上加算モデルと内積モデルは同じ表現能力を持つが内積のほうが計算も早い。
入力の次元が高すぎると、内積モデルそのままでは大きな標準偏差を持つので、で割ることによって解決することができる。
二次形式モデルは一番表現力が高い。
このよう計算したは、が選ばれる確率となるが、どれほどの割合で注目を受けるかということともいえる。それを確率論ではなく、期待値のようにそのまま計算したものがSoft Attentionである。
これと逆なのがHard Attentionというもの。何が選ばれるかを明確に1つだけ選出する。選び方としては、
- が最大のを選ぶ。
- 自体がある確率分布なので、その確率分布の中でランダムに選び出す。
ただし、これでは決定的に選べているわけではないんので、損失関数からの誤差逆伝搬で更新するのはできない。これは強化学習を使わないといけない。というわけで、MLでは誤差逆伝搬で追うことができるように、全部Soft Attentionである。
Key-Valueの構造
すべてのデータについて、のようにキーと値を分離させる。Attentionを計算するのはで、Soft Attentionで合算に使われるのがである。
実際の機械学習ではどのように組み込むのか
Attentionは、
- 何かしらの入力をQuery Vectorとして扱い
- それと一連のデータに対して、あるスコア関数のもとで計算を行い
- Weightとしてのスカラーを得る。
- そのWeightをどう使うかはそれぞれ次第
というものである。この枠組みによって、人間の意図的に集中して○○を見るという部分がうまく学習で実現できる。
Multi-Head Attention
Transformerアーキテクチャでも使われている手法。複数のQuery Vecotorがあるとき、並列的に各Query VectorのAttentionを計算する。各Query Vectorはそれぞれ違うところに注目しており、その結果得られたSoft Attentionの結果もそのまま結合して1つのベクトルにまとめる。(次元を増やしてそのままそれぞれの結果をつなぎ合わせる感じ)
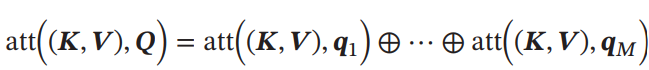
構造化されてるものへのAttention
上下関係が存在するとわかっているものに対して、再帰的にAttentionを適用させてももちろん良い。
Pointer Network(指针网络)
参考: https://blog.csdn.net/qq_38556984/article/details/107574587
従来のEncoder-Decoderモデルでは、Decoderとして得られるベクトルはDictionaryのどれであるかを表すOne-hotベクトルであった。しかし、TSPや凸包を計算するとき、入力される長さは可変なので、出力するone-hotベクトルの次元数も可変になってしまうが、既存のone-hotによるdecodingではそれに対処することはできない。
従来のAttentionは、入力された一連の各サンプルに対して、どれを重視するのかを計算していた。ならば、一番重視しているもの=出力されるもの、とすればone-hotによるDecoderの出力表現とおさらばできる!これがPointer Networkである。(既存のAttentionベースのものは、Dictionaryのone-hotについての確率分布を出力してた)
Pointer Networkの入力にはが与えられ、出力としてが出力され、その値の中身はである。
次の出力が得られる条件付き確率は以下のように近似できる。を直接得る代わりに、がインデックスとして指し示しているを条件付確率として渡す。
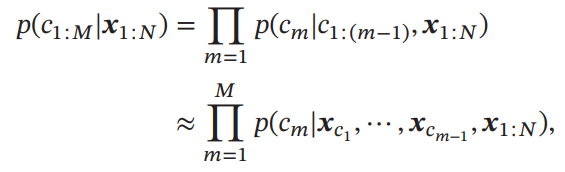
はEncoderの時刻においての入力。はDecoderの時刻においての隠れ層の出力。はAttentionによって計算されたものであり、ここでのスコア関数はRNNの隠れ層の計算のようなものになっている。
ここでは、Softmaxですべてのについてイテレーションしているので、Keyがのものについて、Query VectorがとしてAttentionをしているといえる。そして、そのAttentionによって得られたWeightをそのまま確率に転用しているように学習を仕向ける。ここでは、を学習する。
Self-Attention
長さが一定しない入力に対して、同じ長さの何かを出力するには、CNNやRNNを使えばできる。しかしCNNでは近傍的な関係しかとらえられず、RNNは短期記憶しか持たないのでやはり近傍的関係になる。それはLSTMとしても、性能上の限界が残る。
ネットワークの構造上、長距離の依存関係をとらえるには1. 全結合層を使う 2. ネットワークを深くする がありえる。しかし、訓練コストや訓練データの準備が非常に大変であるうえに、長さが一定ではない入力に対して、全結合層は同じ重みを適用させようとするので難しい。
ここで天才がひらめく。Attentionをうまく使うことで、重みを長さごとに自動生成して変化させれば、全結合層の重みが長さごとに変動できない問題が解決できると。このように、自分自身に対して判断して、現実的には長距離の依存関係を捉えられるようなWeightを生成できるのが、Self-Attentionである。
入力がであるとする。出力はである。これは入力に対して自分自身へのAttentionを行うことで、その結果各に対して何かしらの望ましいというベクトルを得るということ。これは全結合層よりと比べて、異なる長さの入力に対しても異なる重みを(重みを結果的に自動的に生成することで)適用することができ、全結合層さえもしのぐ非常に高い表現力を持つ。具体的には以下のように行う。
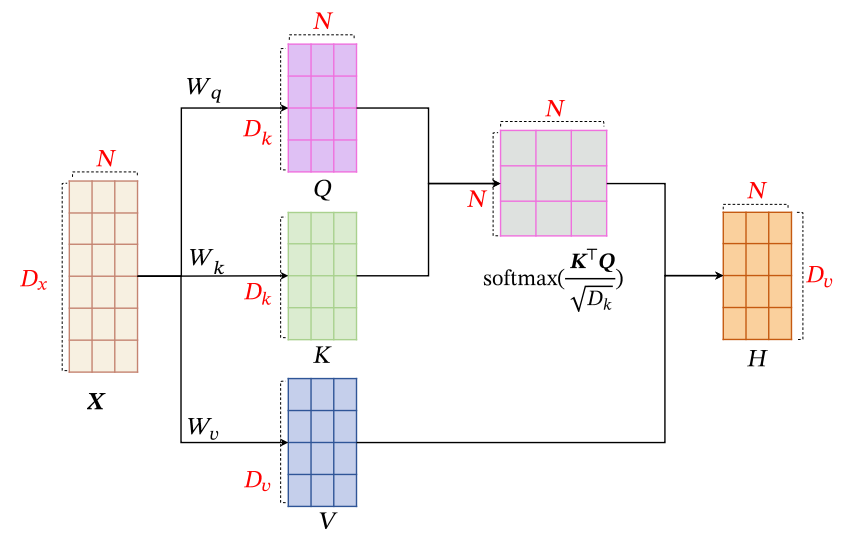
- まず、3つの線形写像によって入力のを写像する。同じ入力からQuery、Key、Valueをそれぞれ個生成する感じ。3つの線形写像はみな学習するパラメタ。
- すべてのに対して、Attentionを行い、soft attentionの結果を得る。なお、よくが使われるらしい。
- このこそが、Self-Attentionという構造によって得たかったもの。
つまり、自分で作ったQueryと自分で作ったKeyを使ってAttentionをして、その結果を使って自分のデータを混ぜる(ようにパラメタを学ばせる)ことで、自分自身のどこを注目するのかを決めさせるという高い表現力を持たせることができる。
このSelf-Attentionについても、複数の3つ組の重み行列によって複数のチャンネルを作ることができ、Transformerアーキテクチャではそれが使われている。
ただ、Self-Attentionはの関連性だけを見るので、どの入力が先か後かはわからない。どんなだろうが同じようなやり方でSelf-Attentionで計算される。どの入力を注目すればいいのはわかるが、注目したのが何番なのかの情報がない。(これは全結合層でも同様にそう。なので、RNNのような順序立った入力を受けるシステムが必要だった)
これを防ぐには、の次元を拡張してそこに位置の情報を追加することが大事。一番簡単なのは何番目かを追加した次元に入れることである。他にも、1番目の値に+1, +2と+(位置)のように入れることである。ただ、これで一応情報は入れてるが、うまく学習してもらえるのはやはり難しい。
そして、Transformerでは、単純に何番目なのかを追加するよりも、三角関数を利用したベクトルを作り、それを本来の入力に加算をしたあとにMulti-Head Self Attentionを行うことで、数学的に高次元に拡張したのでより容易にSelf-Attentionに位置情報付きの前提で学習できるように仕向けている。
Positional EncodingのQiita解説はこちら: https://qiita.com/snsk871/items/93aba7ad74cace4abc62
いずれ自分でもまとめてみる。
外部記憶
RNNの中では短期記憶にとどまってしまう。それを長期的に保持するためにLSTMは別に1つ用意したが、それを拡張して外部記憶のようなDBのようにアクセス専用のものを考えてみよう。
人間の脳で記憶は1つの場所においてるのではなく、広いところに少しずつ置かれているらしい。
そして、人間は
- Working Memory 臨時で覚えるもの。何に使われているかまで覚えている。容量は一番少ない。
- Short-Term Memory 短期的に覚えるもの。容量はちょっと多い。
- Long-Term Memory 長期的に覚えるもの。容量はかなり多い。短期記憶から長期への遷移はEvolutionという。
また、記憶に関しては関係性によって記憶を覚えており、人のことを思い出したら顔や声などが思い返されるというようなものである。
LSTMの長期記憶と比べると、人間の長期記憶はより多くの情報を保存できるうえ、更新されることはあれど、自身を使って他の短期記憶などを更新することはない。
Memory Augmented Neural Network(MANN)
外部記憶という追加の情報を保存する部分を作ることで、ネットワークの記憶能力を増大させる。外部記憶について、Soft Attentionを行うことで、必要な情報を引き出すことができる。
これを利用して3つの典型的なMANNがある。
- End-To-End Memory Network
- Neural Turing Machine
End-To-End Memory Network
読み取り専用の外部記憶とする。に対して、Attentionに使われるKeyはであり、Valueはとする。これは何かしらからいい感じに生成する。
入力に対して、Queryのをメインネットワークが生成する。そして、Attentionを行い得たをもとに、以下のように計算したかったラベルを得る。
これは非常にシンプルな例であるが、次式のように何度もQuery Vectorを更新してその都度Attentionを行ってもよい。
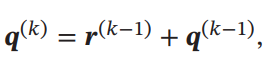
これをMulti-Hopという。毎回Attentionするは同じものでもよいし、別々のものでもよい。同じくから生成されたものであればそれでよい。
Neural Turing Machine
チューリングマシンの説明は省略。気持ちとしては外部記憶をTuring Machineのようにすることで、書き込みや読み取り両方できるようにしたい。
コントローラーと外部記憶という2つの部分からなる。
外部記憶はと定義される。は各記憶の次元数で、は記憶の個数。
コントローラーはDNNかRNNで実現する。
- コントローラーは今の入力、1つ前の出力と1つ前に外部記憶から読み取ったを入力し、今の出力を得る。
- を出力するのと同時に、検索Vector、削除Vector、増加Vectorをより生成する・
- はAttentionに使い、を得る。これは既存のAttentionであり、読み取り操作にあたる。
- 新しいのは、書き取り操作を実現するための削除、増加Vectorもあるということ。(LSTMのGateをより複雑な層で実現した形)
- は個目の記憶へのAttentionの重みだとする。以下のように削除したいと、新たに加えたいを使って更新していく。
Neurodynamicsに基づくAssociative Memory Model
Associative Memory Model=入力された情報から関連する情報を呼び出すためのモデル。
不完全な情報、ノイズのある情報でも連想ができるのが望ましい。
Hopfield Network
隠れ層がなく、自分の出力が自分を含む次の入力に全部使われる再帰的なネットワーク。
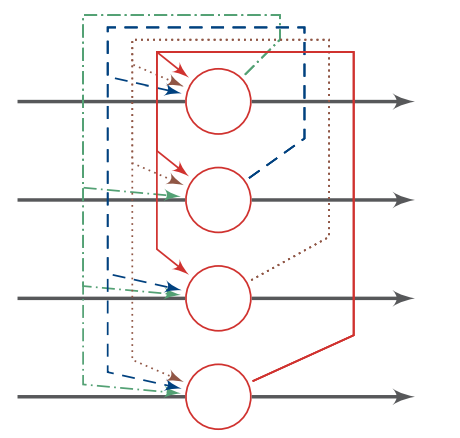
離散版だと以下のように更新できる。重みはが成り立つ。
更新のやり方として、各ニューロンがランダムに1つ1つ更新されていくものと、同時にで一気に更新するのがある。違いとしては、1つ1つ更新だと次のニューロン更新にさっそく今更新したが使われているが、一気に更新だとすべて古いものを使うということ。
この各状態について、HopField Networkはエネルギー関数というものを定義できる。これをIterationしていくと収束することは保証されている。
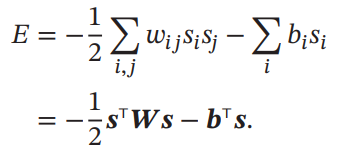
収束した先はエネルギー関数の局所最適解で、Attractorという。複数のAttractorを持つ=複数のパターンを持つ、Attractorへたどり着く動きは検索といえる。Noiseがあっても同じAttractorへ収束すればいいというのは結構都合がいい性質。
