中国の有名な機械学習の本の勉強ノート。自分がわからなかったところだけなので飛び飛びだろう。
ちゃぶ台返しみたいになるが、DNNを実際に訓練する際には2つの難点がある。
- 最適化が難しい 非凸な関数であるので、大域的な最適解を見つけることはほぼ不可能である。また、パラメタが非常に多いので、二回微分を用いた最適な勾配法=ニュートン法などが使えない。そのうえ、勾配消失や爆発が生じやすく、それも最適化を失敗させる障壁となる。
- 過学習する 表現力が非常に強いので、正則化を頑張ることで何とか過学習を防がないといけない。
ちなみに、DNNは理論上(VC次元、Rademacher複雑度などの道具で)非常に表現能力が高くすぐ過学習するというが、学習する情報には後先がある=Memorization Effectがあることが経験的にわかっている。そのうえ、正則化各種正規化の性能は高いということが経験的にわかっている。これをうまいことサポートする理論はいまだにない。
最適化
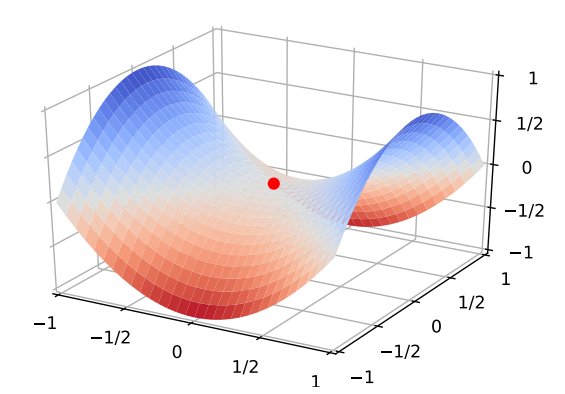
高次元での最適化では、実は鞍点にいるということが非常に多い。そして、勾配降下法は鞍点の近くにいると、停滞してしまい鞍点から離れることができない。なので、確率的な勾配降下法を持ちて鞍点から離れられるようにしていた。
また、DNNでは非常に大量のパラメタがあり、お互いに強い依存関係を持つ(なくていいパラメタ)ことが非常に多いので、各パラメタごとに最終的な損失に寄与する量は非常に少ない。その結果、局所最適解の近くでは、gradientがほぼ平坦な領域=Flat Minimaであることが多い。以下が例。
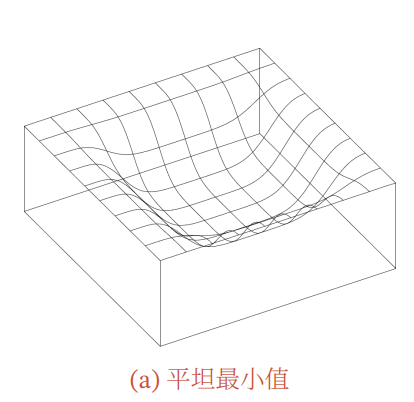
だが、逆に言えば大体平坦ならどれをとってもよいということである。これはロバスト性が高いという意味でもある。
DNNは大きくなるにつれて、局所最適解に陥ってしまう問題は解決されないが、局所最適解だとしても、真の解とほぼ同じぐらい良い解であることが多い。過学習の問題も考えると、局所最適解のほうが逆に良いこともある。
最適化手法の改良
本来はすべてのデータについて勾配を計算して、そこから勾配逆伝搬を行う必要がある。それでは大変なので、以下のような改良をするのが普通。
Mini-batch Gradient Descent
全部のデータではなく、個のデータからなるミニバッチで損失関数を計算し、そこから勾配降下を行って更新し、また次のミニバッチについて同様に計算する。
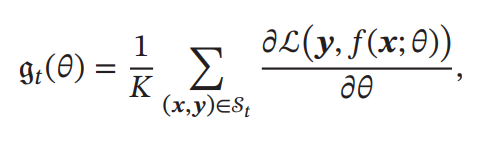
バッチサイズはバッチの分散に影響し、大きいほどノイズの影響が小さくなる。ミニバッチを行う以上、データとして全体を一周した(と期待値的にわかっている)ら、それを1epochだという。
また、研究によって汎化性能とバッチサイズも影響することがわかっている。
- より大きいバッチサイズは、周辺のgradientが鋭い最小値に収束しやすい。
- より小さいバッチサイズは、周辺のgradientが緩やかなflat minimaの最小値に収束しやすい。
学習率の調整
勾配法は基本的には調整しないが、調整するアルゴリズムは存在する。AdaGrad、RMSprop、AdaDeltaなど。
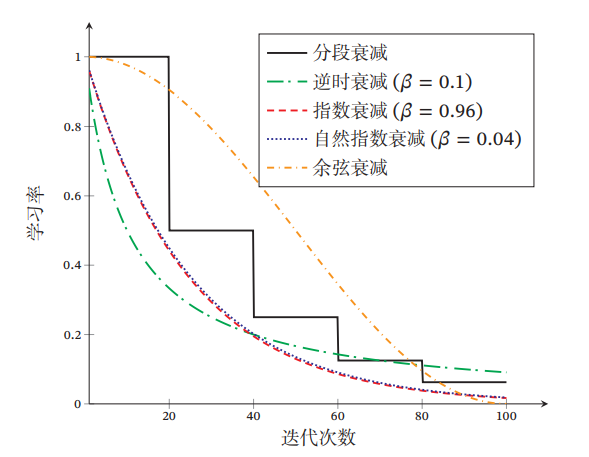
学習率の減少のやり方として以下のような例がある。
- Piecewise Constant Decay(Step Decay) 回のイテレーション経過するごとに、学習率をにすること。
- Inverse Time Decay 時間の経過に従って学習率が下がる。
- Exponential Decay ただし、
- Natural Exponential Decay
- Cosine Decay
学習率のWarm Up
最初はランダムな値で初期化しているので、大きなGradientが予想される。そこに大きい学習率が掛け合わさると、あらぬ方向へと言ってしまう。
以下のようにまずはWarm Upをしてから、学習率減衰をしてもいい。
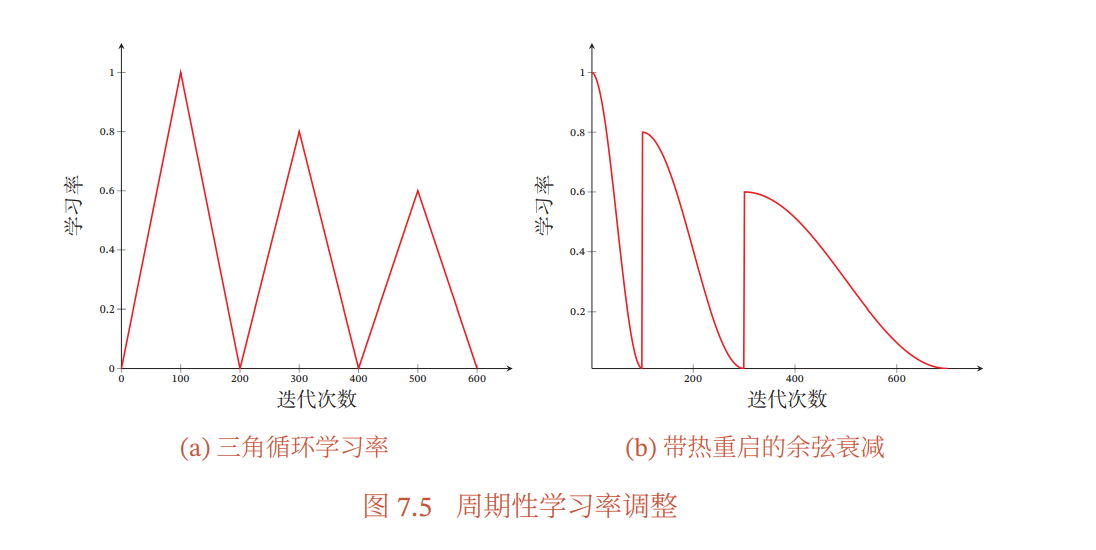
周期的な学習率の調整
経験的に良い性能が出ると知られているのが、周期的に学習率を増やすこと。鞍点の近くでは学習率が大きくてもロバスト性があるので問題がないが、鋭い最小値の周りではすぐに悪い性能を出してしまう。
イテレーション線形に増加し、いてレーション線形に減少するとか。(左図)あとはあらかじめに設定したイテレーションで再起動して、そこからCosine Decayをするとか。(右図)
AdaGrad, RMSprop, AdaDelta
AdaGradという手法がある。を、1から回目のイテレーションまでのGradientの成分の平方値の和だとする。以下の学習率を制御する。は数値の安定性のための小さい定数。
ただ、別にこれは学習が進んでいるかどうかを見て減少させてるわけでは何でもないので、まだ終わってないうちに収束が遅くなってしまう欠点も持つ。
RMSpropは、AdaGradの改善版の1つ。というハイパーパラメタ(0.9とすることが普通)を使って、
このように指数的に減衰させる移動平均をとる。この時、はひたすらに増加するわけではなく、移動平均なので減ったりすることも。
AdaDeltaというAdaGradの改善版もある。をほかのものにした。は、Gradientの前回との差

Gradient Estimationの変更
Gradientに対してどれほど進むのかのみならず、進むべきGradientに手を加える手法もある。
運動量法
毎回のGradientは加速度とみなし、その結果の速度の向きに勾配降下法を行う。という摩擦係数みたいなものを設けて、指数移動平均をとることによって、変な向きを向いたとしても影響を最小化できる。(通例としてがいいとのこと)
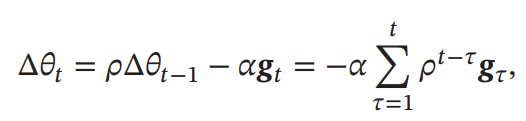
Nesterov法(NAG)
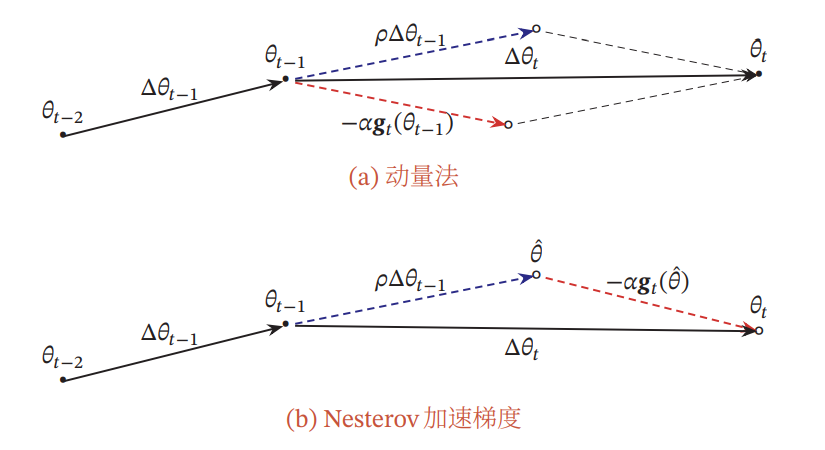
1つ前のGradientを加速度として扱うのではなく、今の速度で進むだろう距離のGradientを加速度として扱う。
Adam
運動両法とRMSpropの組み合わせ知いえる。
RMSpropと同様に、勾配の成分の2乗和の指数移動平均を計算しながら=RMSprop、勾配の1乗和の指数移動平均=運動量法を計算する。
は運動量、は勾配の2乗和。ここでとしている。
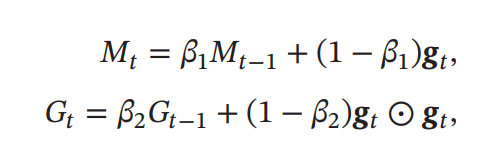
ただし、いずれの2つも0に近いとき、実際から乖離するので、以下のように改善しなければならない。
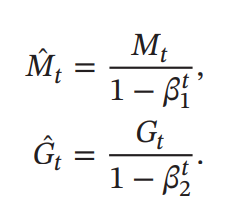
パラメタの更新は以下の通り
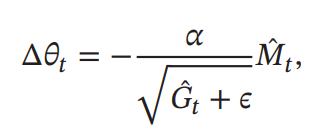
なお、RMSprop+運動量ではなく、RMSprop+Nesterov法の場合、Nadamと呼ばれている。
Gradient Clipping
DNNにおいて勾配消失のみならず、勾配爆発も学習を失敗させる原因である。RNNとかでは実際的に指数的に回数を肩に乗せて計算するので、簡単に爆発しかねなくなる。
Clippingするといっても二種類のやり方がある。
- 値を無理やりに制限する。
- 縮小する。であるならば、そのままにする。そうでないときは、以下のようにする。
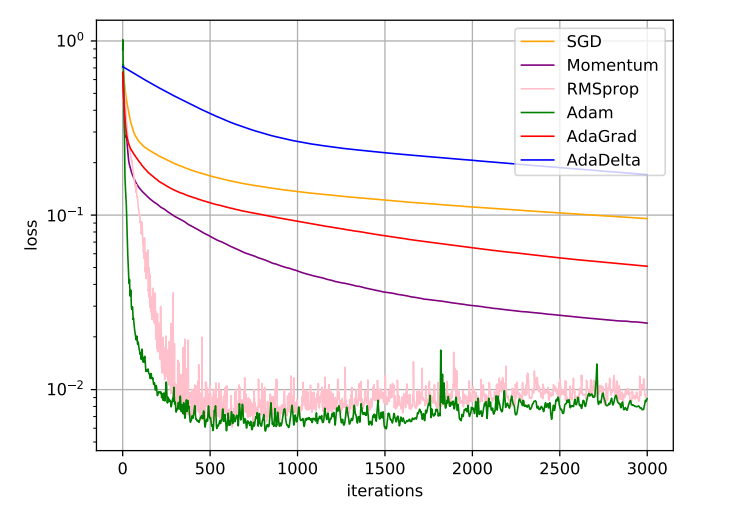
↑おまけ。MNISTに対して各最適化手法の実行結果。
パラメタ初期化
- 最適解に収束できそうな、よさげな値で初期化をする。
- ランダムに初期化。
- とくにDNNではすべてを0に初期化すると、同じLayerのすべてのニューロンは同じ出力を持ってしまい意味がなくなる。
- 固定値初期化。bias=0と固定する。
ランダムに初期化が一番いい。
分散固定した初期化
ある固定した平均値と分散を与えた、指定の分布(ガウス分布、一様分布)で初期化する。
分散を決めるのが難しいのでお勧めしない。
分散をスケーリングしていく初期化
DNNで、活性化関数にSigmoidベースのものを使うとき、あまりにも分散が小さすぎると出力が小さすぎて信号が数層あとに消えるのと、平均0で分散が小さいとsigmoid型はではほぼ線形なので、わざわざDNNにして非線形性を得た意味がなくなる。
そこで、分散をスケーリングしていこう。
以下のようにいろいろ手法がある。は層目のニューロンの数。

直交正規化
気持ちとしては、線形層の変換行列のノルムをと制限したい。
- 期待値0、分散1のガウス分布で行列を生成する。
- その行列を特異値分解し、得た2つの行列のうち、正方行列ならばユニタリ行列にあたるほうを初期値として扱う。
この時ノルムが1に近いまま学習できる。
データの前処理
データの各次元において、同じスケールであることが望ましい。スケールが違うとGradientが不要に敏感になりすぎて、勾配降下法の性能が低下する。
正規化=Normalizationとは、データの尺度をそろえるという意味。一方、正則化は過学習を防ぐため。
やり方としてはいろいろある。Zスコア正規化という、というものがある。
主成分分析(PCA)
データの特徴をとらえたアフィン変換をして、そこから重要ないくつかの次元だけを残して残りを捨てることで、次元を下げつつ情報量をあまり落とさないテクニック。重要な次元=分散が高い。なお、共分散行列は以下のようにも求まる。

このように、平均減算した後に分散を最大化する方向のベクトルをみつけたい。
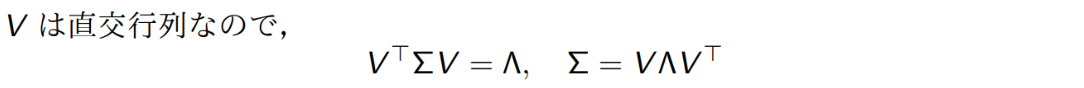
共分散行列は半正定値行列なので、ユニタリ行列で対角化できる。
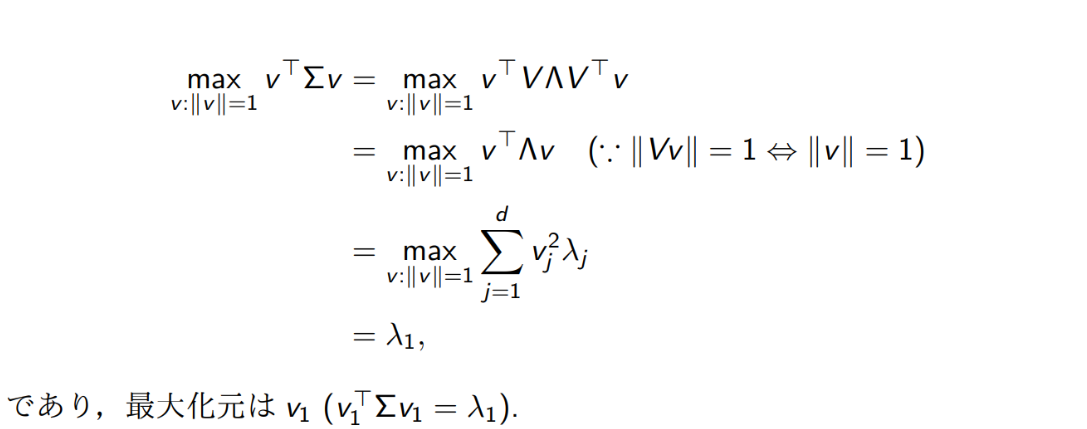
任意の方向のなので、ユニタリ行列を乗じても同じノルムのになり、これの最小化をするといえる。
最大化するには、であるので、最終的には以下のようになる。
とこのように、最大の固有値に対応する固有ベクトルのとなる。

すると、は定数扱いなので次元を1つ落とすことができて、同様に先ほどの問題に帰着することができるので、第二主成分は二番目に大きい固有値に対応する固有ベクトルになる。
そして、半正定値なのですべての固有値は正になるので、固有値全体における選んだベクトルの固有値の和の割合こそが寄与率となる。
なお、この時次元ごとの分散を割って正則化してあげれば、超きれいな多次元分布になるはずである(分散1)。これをWhitningという。
Layer-wise Normalization
各層への入力を、その都度その都度正規化する感じ。
毎回正規化すれば、入力を標準正規分布近くに保証することができるようになる。この時、入力の分布が層を追うごとに違ってしまう問題=Internal Covariate Shiftを改善できる。これによって、Sigmoid関数などで層を追うごとにどんどん1に近づいて傾きが消える問題なども原理的には消え、ちゃんと活性化関数の傾きがsensitiveになるようにすることができる。
いくつかのLayer-wise Normalizationが存在する。
自分向けメモ: 結局複数の層にわたってその出力すべてを見て正規化するのは存在しない!
参考: https://qiita.com/jun40vn/items/2105467cea35f179ea45
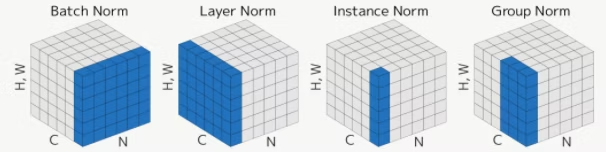
平均をとるとはつまり、そこをイテレーションしていき平均を計算することを指す。
| バッチ内 | チャンネル(各成分)うち | 画像のサイズ | |
| Batch Normalization | 平均をとる | 個々で独立に計算 | 平均をとる |
| Layer Normalization | 個々で独立に計算 | 平均をとる | 平均をとる |
| Instance Normalization | 個々で独立に計算 | 個々で独立に計算 | 平均をとる |
| Group Normalization | 個々で独立に計算 | 一部のチャンネルだけで 平均をとる | 平均をとる |
Batch Normalization
先ほど述べたのがまさにこれ。具体的に説明する。以下のようにDNNの層が与えられる。
ここで、に対してZ正規化を行う。(に対して行っても計算後ずれてきそうだ)
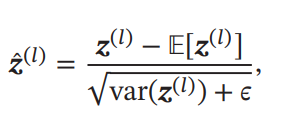
ただ、純粋にこれをやると値は0付近に行ってしまう。Sigmoid型の活性化関数を使うとき、それはつまりほぼ線形変換になってしまう(0の近くはほぼ線形になるので)という問題を持つ。これを解決するために、以下のようにZ正規化に線形変換を加える。Z変換のための平均と分散は、同じ層のすべてのチャンネルの間(つまりすべての入力)で計算される。
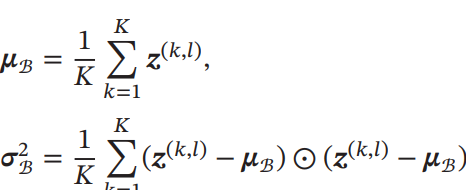
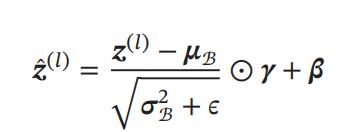
実際、ここまで行うことによって、実質的には通常の線形層(バイアスはない)のあとに、Z正規化+線形変換という層(線形変換のパラメタは学習対象)を新たに足しているのに等しい。バイアスを「Z正規化+線形変換」で内包化しているので、以下のように通常の層ではバイアス項は不要になる。
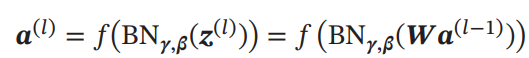
よく見ると、バッチの数と高さと幅のでイテレーションして平均をとっている。
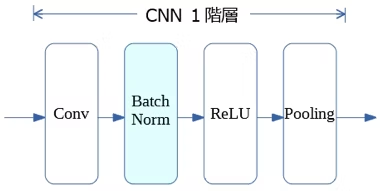
入れる場所は畳み込み層ではこのようになっている。
Batch Normalizationは最適化をしやすくするだけではなく、一種の正則化の効果をもたらすこともできる。バッチごとにやることで、他のも参考するようになり、いくつかのサンプルだけに過学習をさせないようにすることができる。
Layer Normalization
Batch Normalizationは、バッチサイズが小さいと逆効果という欠点を抱えている。また、RNNのように各層で重みを共有する場合、毎回同じパラメタで正規化もできないので本質的にはBatch Normalizationができない。
代わりに、同じチャンネルの層の出力(1つのチャンネルだけ)について、で正規化を行う。式は同様に正規化+線形変換である。ただし、Batch Normalizationと違って、1つのデータだけについて、そのデータの各次元(各チャンネル)の平均や分散をとって、各チャンネルの値を正規化している。
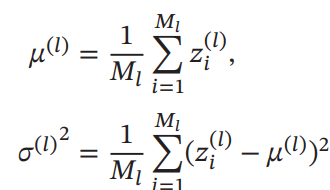
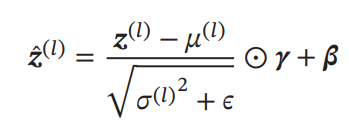
チャンネルの数と高さと幅でイテレーションして平均をとっている。なので、でもかまわないということ。
RNNでLayer Normalizationを簡単に適用できる(なんせ1つのサンプルの成分だけ見ればよく、過去のデータなど見なくてよいので)
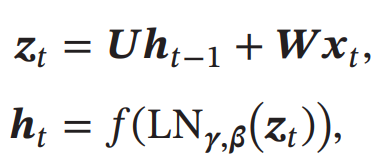
余談だがここでのLayerはむしろチャンネル。本当にDNNのLayerごと正規化するのは、Weight Normalization。
Instance Normalization
高さと幅でイテレーションして平均をとっている。
つまり、各チャンネル、各データはそれぞれそのままで独立している。
欠点としては、複数のチャンネルの組み合わせによってあらわされる特徴をうまくとらえられない。
Group Normalization
高さと幅だけでなく、一部のチャンネル(すべてではない)でイテレーションして平均をとっている。
一番よさそう。やり方次第では、Batch Normalizationに匹敵するらしい。
Weight Normalization
参考: https://blog.csdn.net/hxxjxw/article/details/124071198
先ほどの4つはDNNの層を跨がなかったが、今回は層を跨いで各層の重みを正規化する。LSTMとNoiseに敏感なモデルに対して高い性能を持つ。
もともとの層での重み行列に対して、次のように再定義する。は行目である。は学習するパラメタであり、各層の間で共有されるものである。2つの学習パラメタに分割することによって、SGDが早くなるらしい。
いい性能を出すためにはいい初期値をあてがわないといけないという問題を持つ。
Local Response Normalization(LRN)
参考: https://developers.agirobots.com/jp/blog-lrn-cnn/#:~:text=LRNとは畳み込みニューラル,を防いでいます。
あるフィルタによって、チャンネルが得られる。このについて、として、とすることができる。以下のように近傍をみて正規化を行う。
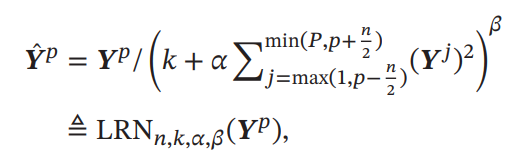
はハイパーパラメタである。気持ちとしては、近隣のチャンネルの値が大きければ、今のフィルタが全体的に小さくなる。これは生物学的に、1つのアクティブなニューロンのまわりのニューロンはアクティブではないことが多いというところから示唆を得ている。
ハイパーパラメタチューニング
魔法です。組み合わせ最適化問題なので離散的であり、SGDによって解くことができない。あとは各パターンをそれぞれ試すのは非常に難しい。
Grid Search(网格搜索)
すべてのありうるハイパーパラメタの組み合わせを試す。
Random Search
全部総当たりではなくいくつかランダムのものを選んでそれでやればよし。
Bayesian Optimization
すでに行った情報から一番最大の収益をもたらす次の組み合わせを計算してそれを試す。
がガウス過程に従うとすると、はガウス分布となる。ベイズ最適化では、すでにある経験結果からガウスモデルを推測し、事後分布を求める。
ベイズ的に地ゴン分布をうまく推定するにはは十分に経験が多くないといけないが1つ1つのコストが高すぎる。その結果、ある収益関数でそのが十分によいかを評価する。一番よくつかわれるのはExpected Improvement=EI
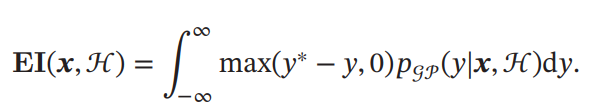
ベイズ最適化の欠点としては、共分散行列の逆行列の計算で時間を食うこと。
Dynamic Resource Distribution
これ実は強化学習の問題ともみなせて、Multi-arms bandit problemとみなせる。
1つのアルゴリズムとして以下のようなものがある。
- N組のハイパラを試すとする。
- 計算資源をN組にそれぞれに以下のように分ける。Tは何回目のループか、は資源の総数。は今の組み合わせの数。
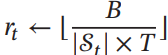
- その中で一番性能が良かったものを半分取り出して、2に戻る。
- 1つだけ残ったら終わり。
Neural Architecture Search(NAS)
1つの制御ネットワークから、子ネットワークを生成する構造。その子ネットワークを最終的に使う。これは強化学習で行い、rewardはその子ネットワークのAccuracyでOK。結構未知の分野らしい。
ネットワークの正則化
過学習を防ぐために、損失関数やネットワークの構造自体に手を加えておくことを正則化=Regularizationという。
DropOutについても述べているが、わかっているのでさすがに跳ばす。
L1, L2, Linf正則化
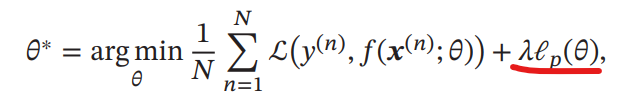
ハイパーパラメタを使って、正則化項を加算することで学習のパラメタの動き方を仕向ける。
L1損失はそのままではでは微分不可能(絶対値関数なので)なので、よくで代用される。
- L1正則化は、パラメタを尖鋭化、sparseにさせる。
- L2正則化は、パラメタをまんべんなく使う、大体似たような値をとらせる。
L1とL2正則化を同時に導入する手法もあり、それはElastic Net Regularizationという。
Weight Decay
パラメタの更新は普段ならばになっている。しかし、ここではハイパラのを導入し(0.0005などの小さい値とする)以下のようにしている。
SGDでは、L2正則化の項を微分するとWeight Decayそのものである。他の複雑なもの(Adamなど)では等価ではなくなるけど。
Early Stop
過学習をする前に止めておくという非常に良い考え。Validation SetのAccuracyが下がってきたらそこで止める感じ。ただし実際の学習曲線は局所的に振動しているのでうまいこと指標で見極めないといけない。
RNNのドロップアウト
普通のドロップアウトはわかってるので跳ばす。
RNNでドロップアウトを使うとき、各状態ごとを飛ばすのはよろしくない(記憶の伝播の流れが切れてしまう)
解決法として、RNNで記憶をつなげる部分にはドロップアウトせず、入力や出力の部分のDNNにはドロップアウトを行う。
たぶん: 記憶を丸ごとドロップアウトするのはまずいが、記憶の重みの一部だけドロップアウト(もちろんすべての時間において同じようなところを欠けさせることが大前提)
Data Augmentation
学習データを特定の操作でかさ増ししてロバスト性を獲得させる。画像の場合、回転、反転、拡大縮小、平行移動、Noiseを加えるなどがある。
Label Smoothing
one-hotのラベルをそのまま目的だとすると過学習してしまうので、そこまでとがってないone-hotっぽいベクトルのように平滑化をすることを指す。
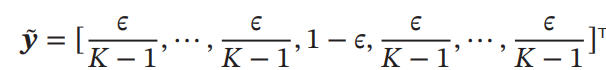
そのように平滑化したものは、Soft Target(软目标)と呼ばれている。
Label Smoothingの一つの応用として、複雑な(複数のネットワークを含む)教師ネットを訓練しておく。そのネットワークの出力を使って(本来のone-hotのターゲットではない)Student Netを訓練する。これによって、Studentは小さいサイズで、教師ネットをトレースできて、知識蒸留=Knowledge Distillationされる。これも教師ネットの出力はSoft Targetと考えられ、Student Netは過学習しづらい(というか極端なone-hotではないので学びやすいのかな?)。
