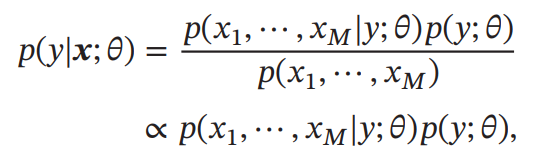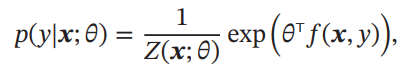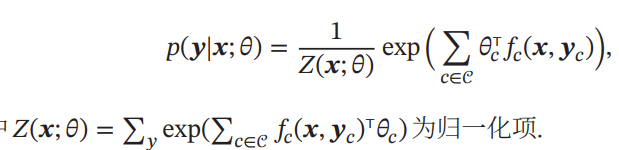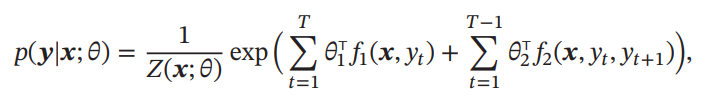NNDL 第11章独立した複数のモデルの訓練による効用

中国の有名な機械学習の本の勉強ノート。自分がわからなかったところだけなので飛び飛びだろう。

https://nndl.github.io/

モデルの表現有向グラフィカルモデル有向グラフィカルモデルを実現するには Sigmoid Belief Network(SBN)Naive Bayes Classifier 隠れマルコフモデル無向グラフィカルモデル無向グラフィカルモデルのクリーク分解一般的な無向グラフィカルモデルを実現するには対数線形モデル Conditional Random Field(CRF)有向と無向の間の転換グラフィカルモデルの学習

Graphical Modelとは、変数間の依存関係を定式化したもの。パラメタにすべて依存関係が存在するのであれば、大量にサンプリングしないといけない。これに対して、独立性の仮定を設ける。 $x_1, \cdots. x_n$ に対して、

$x_1$ を知っている前提で、 $x_2, x_3$ は独立である。

p(x_2, x_3 | x_1) = p(x_2 | x_1) p(x_3 | x_1)

$x_2, x_3$ を知っている前提で、 $x_4$ と $x_1$ も独立である。

p(x_1, x_4 | x_1, x_3) = p(x_1| x_2, x_3) p(x_4 | x_2, x_3)

これを依存関係で構築すると、以下のようにできる。

p(x_1, x_2, x_3, x_4) = p(x_1) p(x_2|x_1) p(x_3|x_1) p(x_4 | x_2, x_3)

Graphical Modelでは3つの基本的な問題がある。

どのようにGraphical Modelで構成するか。
どのようにパラメタを学習するか。
既知の変量をもって、どのようにほかの変量の確率分布を計算するか。

実際ほとんどの機械学習はGraphical Modelで表示することができる。それはそう。

例えば普通のCNNで識別するならば、 $X \to \mathbf{y}$ となるし、中に隠れ変数 $\mathbf{h}$ があるならば、 $X \to \mathbf{h} \to \mathbf{y}$ というようになる。基本は一本線。

モデルの表現

有向グラフモデルと無向グラフモデルに分けられる。

有向グラフモデルの場合、DAGで構築される。 $A \to B$ は $p(B|A)$ となる。
無向グラフモデルの場合、無向グラフで作られる。辺があるということは依存関係があるが、どちらかが原因で結果かはわからない。

有向グラフィカルモデル

有向グラフィカルモデルは、Bayesian Network、Belief Networkとも呼ばれている。上で紹介したかたちが、有向グラフィカルモデル。

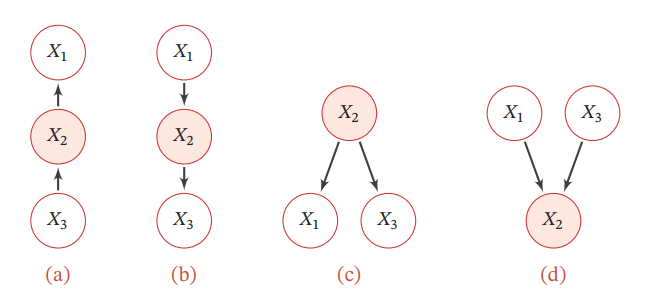
3つによる因果関係として、以下の4つの図のタイプがある。 背景に色がついているのは観測されているパラメタである。

aからcはすべて、 $X_2$ が既知の時、 $X_1, X_3$ は条件付独立。

dだけ、 $X_2$ が未知の時、 $X_1, X_3$ が独立だが、知ってしまったら独立ではなくなる。

局所的マルコフ性という性質がある。任意の変数について、１つの親接点が定まったら、すべての子接点以外のものとは条件付独立というもの。

有向グラフィカルモデルを実現するには

Sigmoid Belief Network(SBN)

変量が $X_k \in \{0, 1 \}$ をとる。親節点の集合は $\pi_k$ だとする。シグモイド関数を $\sigma$ で表す。条件確率分布は以下のようになる。

Pr(x_k = 1 | \mathbf{x}_{\pi_k}; \theta) = \sigma(\theta_0 + \sum_{\mathbf{x}_i \in X_{\pi_k}} \theta_i \mathbf{x}_i)

つまり、線形モデルをSigmoidに入れた感じ。前にも同じような線形モデルによるcalibration=Logistic回帰があった。📄NNDL 第3章線形学習

学習するパラメタは $\theta$ である。親節点の数が $M$ 個ならば、単純に $2^M$ 個パターンの条件が生まれ概算が面倒である。だが上のようにパラメタ化することで、 $M+1$ 個のパラメタで事足りる。

つまり、1つの頂点への入力をすべてまとめて1つのsigmoidのモデルで近似している。

1層のみ含むSigmoid Belief NetworkとLogistic回帰モデルの違いは、前者で $x$ は非確定の変数で分布自体を推定して、生成モデルになれる、後者は確定の値で、分類モデルとなる。

Naive Bayes Classifier

ベイズの定理により、以下が成り立つ。

仮定として、 $Y$ が与えられたとき、 $X_m$ 間はすべて条件付独立であるとする。この時、以下のように $p(y|\mathbf{x})$ を分解できる。ここで $\theta_c$ は事前分布のパラメタであり、 $\theta_m$ は条件分布のパラメタ。

p(y|\mathbf{x} ; \theta) \propto p(y | \theta_c) \prod_{m=1}^M p(x_m | y ; \theta_m)

離散分布ならば、 $p(x_m | y;\theta_m)$ は多項分布、連続分布ならばガウス分布でモデリングできる。

つまり、Graphical Modelの各Edgeごとに1つの分布を仮定し、独立性を仮定しているので積で計算している。

見るように、これは非常に強い独立性の仮定を設けているが、実用的にはNaive Bayes Classifierは悪くない結果を出す。

隠れマルコフモデル

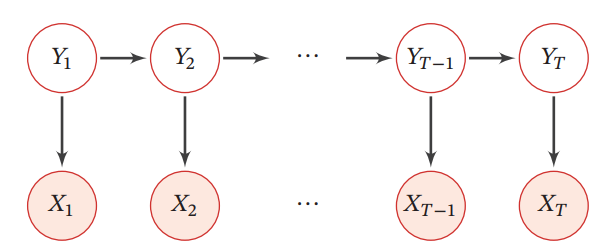
$X_1, \cdots$ は観測可能な変量であり、 $Y_1, \cdots$ は隠れ変量である。これらはすべてマルコフチェーンを形成し、 $X_t$ の観測は当該時刻の隠れ変量 $Y_t$ に依存するマルコフ過程に従う。

これを式で定義すると以下のようになる。 $X, Y$ はベクトルをつなげたもの。式の中では、 $y_t$ をそれぞれどのように作っているか、そして各 $y_t$ から $x_t$ ができる確率を計算している。

p(X, Y; \theta) = \prod_{t=1}^T p(\mathbf{y}_t | \mathbf{y}_{t-1}, \theta_s) p(\mathbf{x}_t|\mathbf{y}_t, \theta_t)

$p(\mathbf{x}_t | \mathbf{y}_t, \theta_t)$ は出力確率といい、 $p(\mathbf{y}_t | \mathbf{y}_{t-1}, \theta_s)$ は遷移確率という。

無向グラフィカルモデル

全体的な解説: https://www.slideshare.net/Kawamoto_Kazuhiko/ss-35483453

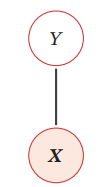
無向グラフィカルモデルはマルコフ確率場Markov Random Field(MRF)、Markov Networkとも呼ばれてる。

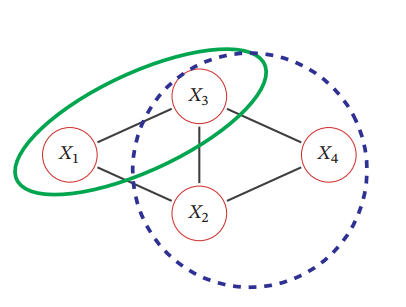
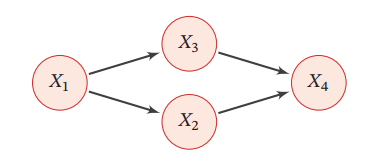
ランダム変量 $X_1, \cdots, X_N$ について、それを頂点とした無向グラフ $G=(V,E)$ を定義する。頂点 $v \in V$ に対して隣接頂点を $\mathcal{N}(v)$ を定義する。この時、各頂点が局所的マルコフ性を満たす=隣接している頂点以外とは独立で関係がない。

p(\mathbf{x}_k | X_{\neg k}) = p(\mathbf{x}_k | X_{\mathcal{N}(k)})

上のようなグラフの場合、 $X_2, X_3$ が既知であるとき、 $X_1$ と $X_4$ は互いに独立である。また、 $X_1, X_4$ が既知であるとき、 $X_2$ と $X_3$ も互いに独立である。

無向グラフィカルモデルのクリーク分解

DAGではないので、トロポジカル分解はできない。その代わりに、Clique=クリークという、集合内のすべての頂点の間に辺がある=完全グラフというものに分解していく。上の図の場合、以下のようなクリークを持つ。

(X_1, X_2), (X_1, X_3), (X_2, X_4), (X_3, X_4), (X_2, X_3), \\ (X_1, X_2, X_3), (X_4, X_2, X_3)

その中で、極大のCliqueに着目する。他に何かの頂点を加えてもCliqueを新たに作れない=極大Clique。この時、別にクリークのサイズが最大と等しいわけではないことに注意！上図の例だと、 $(X_1, X_2, X_3), (X_2, X_3, X_4)$ が極大クリークの集合。

そして、無向グラフィカルモデルの分解を以下のように定める。

与えられた無向グラフの極大クリークの集合を $C$ (1つとは限らないので)とする。
- 最大クリークの集合ではない！極大クリークとは、任意の頂点を加えてもより大きいクリークを作ることができないクリークの集合。
クリーク $c$ について、 $\phi_c(\mathbf{x}_c)$ はPotential Functionという。
- 各クリークごとに変わる势能函数Potential Functionに頂点を代入している。
- 一般的に使われるのはギブス分布。量子力学のルールで習慣的にマイナスをつけているだけ。 $E_c$ によって毎回変換しているといえる。
$\phi_c (\mathbf{x}_c) = \exp(- E_c( \mathbf{x}_c))$
$Z$ はPartition Functionであり、総積を確率化したいから割っている。

p(\mathbf{x}) = \frac{1}{Z} \prod _{c \in C} \phi_c (\mathbf{x}_c) \\ Z = \sum_{\mathbf{x} \in X} \prod_{c \in C} \phi_c(\mathbf{x})

もしギブス分布に従うと定義するのならば、以下のように書くことができ、それはボルツマン分布というもの。

p(\mathbf{x}) = \frac{1}{Z} \prod_{c \in C} \exp(-E_c(\mathbf{x}_c)) = \frac{1}{Z} \exp(- \sum_{c \in C} E_c(\mathbf{x}_c))

このようにモデリングするのが普通である。

一般的な無向グラフィカルモデルを実現するには

対数線形モデル

Potential Functionを以下のように定義する。

\phi_c(\mathbf{x}_c | \theta_c) = \exp(\theta_c ^ T f_c(\mathbf{x}_c))

$f_c(\mathbf{x}_c)$ は $\mathbf{x}_c$ の特徴量を抽出しているといえる。

このように定義すると、グラフィカルモデル全体の対数確率は以下のようになる。

\log p(\mathbf{x} | \Theta) = \sum_{c \in C} \theta_c ^ T f_c(\mathbf{x}_c) - \log Z(\Theta)

このモデルを用いて、 $p(y|\mathbf{x})$ を予測する場合は以下のようになる。

このモデルでは、 $X, y$ の間の関係は以下のようになる。

Conditional Random Field(CRF)

解説: https://mieruca-ai.com/ai/conditional-random-fields/

上の対数線形モデルでは、 $y$ は定数であったが、その $y$ すら確率変数となるときが、Conditional Random Fieldである。 $p(y|\mathbf{x};\theta)$ は上のセクションのようなギブス分布で定義するとして、以下のように $p(\mathbf{y} | \mathbf{x}; \theta)$ を得ることができる。

この上の式は、すべてのクリーク内での対数線形モデルの総和である。

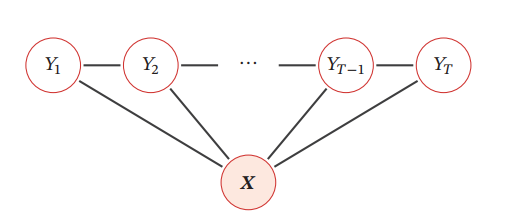
そして、CRFについてグラフをどのように書くかはいろんな定義があるが、最もよく使われるのは以下のようなLinear Chain CRFである。

存在するクリークは $(Y_1, Y_2), (Y_2, Y_3)$ などや $（Y_1, Y_2, X), (Y_2, Y_3, X)$ などの3つ組であり、後者が最大クリークなので、後者に着目する。

$（Y_1, Y_2, X)$ について、 $(Y_1, Y_2)$ の関係は $f_2(\mathbf{x}, y_1, y_2)$ でとらえてこれは遷移特徴、 $(Y_1, X), (Y_2, X)$ の関係は $f_1(\mathbf{x}, y_i)$ でとらえて状態特徴という。

よって、最大クリーク全体についてイテレーションすると以下のようになる。ここで、 $(Y_2, X), (Y_4, X)$ などは各クリークから2回ずつ呼ばれるが、どうせパラメタと内積をとるので1つにまとめていい。なので以下のようになる。

有向と無向の間の転換

無向から有向に直すのは難しいが、有向を無向に直すのは簡単である。

無向は最大クリークで見るので、1つの最大クリークの中に収める必要がある。このために辺を追加することになるが、それをMoralizationという。