中国の有名な機械学習の本の勉強ノート。自分がわからなかったところだけなので飛び飛びだろう。
ラベルやフィードバックが一切ない状況下で学習をなんとかする手法。以下の数種類に分類できる。
- Unsupervised Feature Learning ラベルがないデータから有効な特徴や表示を得たい。次元低下、データ可視化、データの前処理などで使われる。
- Probabilistic Density Estimation 与えられたサンプルから、サンプル空間の確率密度を推定する。(ParametricとNon-parametricがある)
- Clustering 与えられたサンプルを、一定のルールに従って複数のClusterにカテゴリ分けしていく。
Unsupervised Learning
PCAについてはこちらの通り。
Sparse Coding(稀疏编码)
参考: https://www.slideshare.net/slideshow/sparse-codingpcaica/231946611
生物学的には、網膜でとらえられた画像はそのまま上位の認識機構に入るのではなく、なにかしらの基底と係数ベクトルの積(にノイズが少し加わって)となって、その係数=Codingが伝達されるらしい。これによって、各ニューロンはエッジ、特定の模様だけに反応するようになっている。
数式で表すと、個の正規直交基底が存在し、それを列ベクトルとして並べたものがとなり、これをDictionary(辞典)という。ここで、係数ベクトルを得ることができ、これをEncoding=编码という。
主成分分析によって、Encodingをしているといえる。しかし、それは各正規直交基底と掛け合わせた係数ベクトルは疎ではない(各次元に値ががっつり入っている)。疎となるようなEncodingを得たい。
正規直交基底では、既定の数と同じだけのちょうどの次元のヒルベルト空間を作っていた。ここで、過完備(線形従属を含む基底の集合)なものをあえて使うことによって、うまく基底から疎なEncodingを作れれば、人間には理解しやすくなる(既定の疎の成分は寄与を考慮しなくていいので)。そのうえ、過完備である以上複数のEncodingが存在するが、そこにさらなる制限を加えることで、過完備で無限の表現ができたEncodingから唯一となるEncodingを得ることもできる。
実際にはノイズ除去などで使われたり。PCAだけでは、複数の分布の合成にもバカ正直に最適化するので結果として全く実像を表してない基底になってしまうことがある。これに対してSparse Codingするなら、過完備なので複数本の基底で結果的に複数の分布の特徴もうまくとらえるポテンシャルがある(余分な基底を使っていいので、複数の分布それぞれに適した基底を用意したりすることも理論上可能)
入力が与えられたとする。次のように目標関数を定義する。
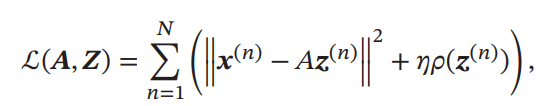
は評価関数であり、ハイパラによってsparse性の強さを制御する。Encodingを得たい中、過完備なのでこのままでは複数のが0をとるEncodingが存在する。それを次元面からも(実質と線形独立となるベクトルを入れていくとか)?、パラメタの大小からも制御するのが評価関数の役割。
評価関数はつまりL0ノルムを使うのが一番簡単であるが、最適化ができないので、
- のL1ノルム
- の対数関数
- の指数関数
が使われてたりする。
学習方法
交互にとを最適化することで、過完備な基底とEncodingを同時に得ることができる。
- を固定して、を最適化。
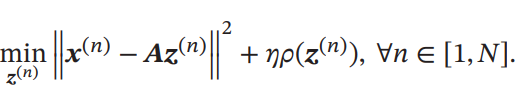
- を固定して、を最適化。
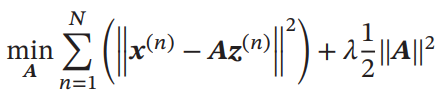
Auto-Encoder(自编码器)
として、次元の特徴量をうまく次元に圧縮したい。この時、
- Encoderとして
- Decoderとして
学習の目標は、合成写像をかませて低次元に表現力を限定させたときに落ちる情報量を減らしたい。以下の損失関数を使う。
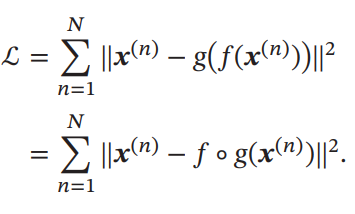
これを実現するとき、1層の隠れ層を持つNNということになるが、の持つ重みをとすると、の重みをとすることで、Tied Weightということとなり、表現力を意図的に落とすことで、学習しやすくさせて、正則化にもつながる。
Tips: この本では最初にEncoder-Decoderモデルを紹介したとき、RNNを使ったものを紹介していた。だがEncoder-Decoderモデルは入力から何かしらの別の出力が得られればそれでよく、RNN、Transformer、CNNなど実現するためのアーキテクチャはなんでもOKである。
Sparse Auto-Encoder
先ほどのAuto-Encoderは低次元の表現を学習させていた。もし高次元のを学習させても無限の解があるので特に意味がないが、ここでSparse Encodingのあの損失関数の式をそのままNNに学習させることで、Encodingがsparseになるという意味を持った高次元での表現を得ることができる。
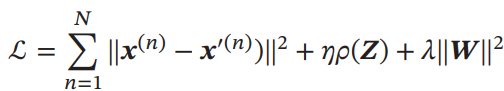
この損失関数をNNによって最小化させていく。NNの重みはTiedであり、はEncoderのアフィン変換行列の重み。
ここで、は先ほど定義したものを使ってもよいし、NN特有の「隠れ層の各ニューロンのActiveとなる確率」と扱ってもよい。をその確率というものと扱える。そして、事前にを指定する(どれほどActivateになるかを指定する感じ)ことで、KLダイバージェンスを評価関数に出k理宇。
ものによっては、複数層からなるものでやってもよい。
Denoising Auto-Encoder
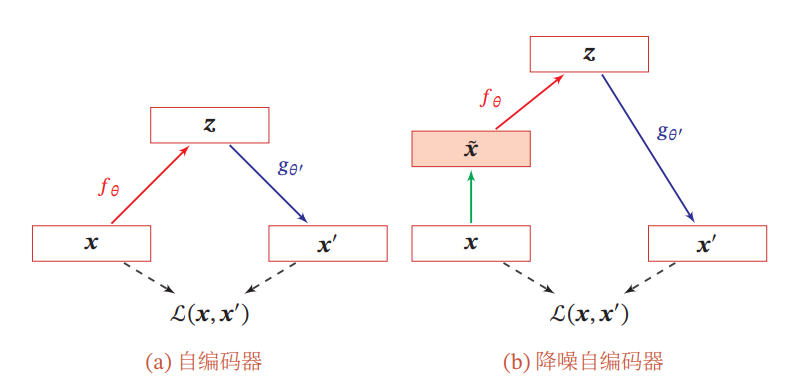
ロバスト性を高めるために、わざとNoiseを加えたうえで復元できるようする。高次元の画像などのデータでは冗長性は持っているのでこれは結構有意義なアプローチである。左が普通のAuto-Encoder。右がノイズを加えたDenoising Auto-Encoder。
確率密度推定
観測されたサンプルから、確率密度関数をうまく推定したい。
パラメトリック密度推定
事前知識によって、特定の分布に従うとまず仮定し、そのパラメタを推定するということなる。
パラメタに従ってデータが得られたとすると、以下のようにサンプルを得るための確率の対数尤度は以下のようになる。
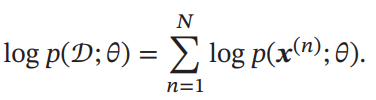
正規分布、ディリクレ分布だとそれぞれ明示的に数式で解くことができる(略 前自分のノートに合ったのでさすがに書かない)
しかし、この手法は現実的には以下のような問題を抱えている。
- モデル選択問題 現実の分布はかなり複雑なのでうまく表せていない可能性が非常に高い。」
- 観測不能変量の場合 観測不能な隠れパラメタは重要だが、それを捉えることはできない(EMアルゴリズム
- 次元の呪い 高次元のデータのパラメタの推定は非常に難しい。過学習が簡単に起きる。
ノンパラメトリック密度推定
個のサンプルのうち、確率で想定の区間内に現れるときは、二項分布に従う確率となる。は想定区間内に実際に現れたサンプルの数。
二項分布の性質上となる。が十分に大きいときは、と仮定することができる。(仮定1)
また、の確率で想定の区間内に出現する条件は具体的にはであるが、十分にが小さくその中で一様分布に近似できるという(仮定2)。このとき、の体積をだとすると、が成り立つともいえる。この2つの仮定によって次の等式を得ることができる。
この式でうまく推定するときには、を大きくしてを小さくしたい感じ。しかし、実際はそれだと十分にサンプルが集まらないので、以下のような手段が一般的。
- の大きさを固定して、体積の各セクションに含まれている数を数える。
- の大きさを各セクションごとに変更して、どのセクションにもちょうど個のサンプルが含まれるようにしたい。
区間のサイズ固定する手法
1の方法。実現させるにはヒストグラムを使ってもいいが、必要サンプル数が次元の呪いに直面する。ここでは、Kernel Density Estimationという手法を使うのが良い。
次のように、Kernel Functionを定義する。右辺の意味はサンプルが各次元においてしっかりと区間内に収まっているかどうかの指示関数である。
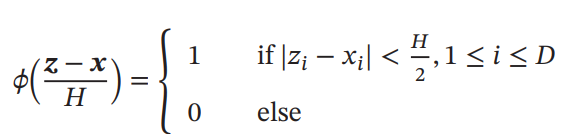
個のサンプルが与えられたとき、上のKernel Functionを使うことでサンプル数を計算できるので、密度関数の計算もできる。は超立方体の体積。
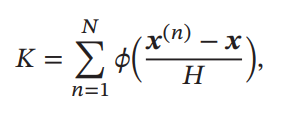
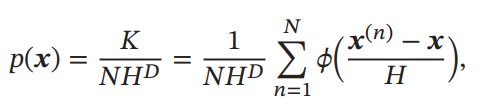
ここでは超立方体によるKernel Functionを選んでいるが、正直扱いにくい(微分できないし…)。そこで、Gaussian Kernel Functionを使うこともできる。
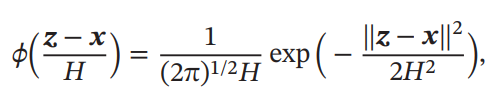
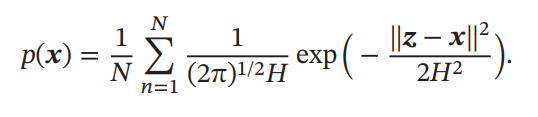
k Nearest Neighbor(kNN)
超立方体のサイズを固定しちゃうと、密度の高低によって過疎、過密が起きてしまう。そこで、についての密度を知りたいときは、を中心にした超球体を選び、ちょうど個のサンプルがそこに入るようにする。そこから、を用いて計算するのである。
つまり、の周辺個のサンプルを見ることになり、その中で最も確率が高いもの=最も多いクラスをそのラベルとして扱うという応用ができる。となったとき、分類誤り律はベイズ分類器の2倍よりは悪化しないことが証明されているらしい。
ただ、現実的にはは選び方次第でかなり変わるアルゴリズムでもある。小さすぎると密度推定ができないし、大きすぎると過度に大域的にとらえてしまう上計算コストも高い。
