中国の有名な機械学習の本の勉強ノート。自分がわからなかったところだけなので飛び飛びだろう。特に線形学習は大体わかってるし。
やらないとやはりヤバい。存亡の際に立っている認識で臨む。
線形分類器と識別境界
線形識別器は、。これが妥当な重みが存在して完全に分類できるときは、線形分類可能という。
多クラス分類
カテゴリがみな個あるとする。特徴量は次元。
- 1 vs other。個の識別器を作って判断する。
- 1 vs 1。個の識別器を作って、すべてのありうるカテゴリのペアで作る。
- argmax。識別結果としてスカラーを出すのではなく、次元のベクトルを出して、各成分ごとにそのカテゴリに所属していることに対しての評価値(正ほど良い)。これを実現するためにはのベクトルではなく、の行列とすればいい。実質的には個の識別器を同時に訓練している。
- これが一番いいです。
- argmaxで分類できる場合、多クラス線形分類可能であるという。
Logistic回帰
線形識別器をロジスティック関数に入れたもので、事後確率を近似する試み。
式変形するとこうなる。logの中身は、Oddsという。log OddはLogitという。
なので、Logistic回帰は、Logit回帰とも言われたりする。
Logistic回帰の学習については、クロスエントロピー誤差によって勾配降下法で行う。式変形をすると以下のように導関数は明示的に得ることができる。二次導関数も明示的に求まるので、ニュートン法でもいい。
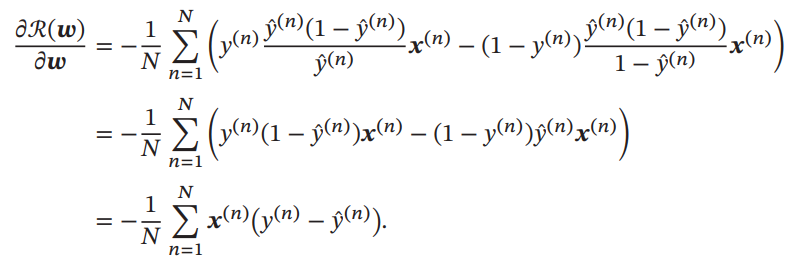
Softmax回帰
多クラスのLogistic回帰ともいえる。
の時とみなせるので(バイアス項はベクトルの中に折りたためる)、Logistic回帰とも兼ねている。
これの学習も同様にクロスエントロピー誤差によって行う。明示的にできるので、以下のようにLogistic回帰と似た形になる。は各という行ベクトルを各列に並べたもの。
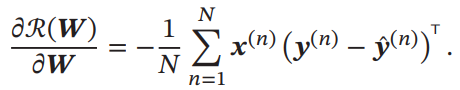
パーセプトロン(感知器)
最も簡単なニューラルネットワークのニューロン。ここでは同様にバイアスは重みの中に折りたたんでいることに注意。
間違った分類がなされた時、誤差逆伝搬するとgradientは明らかになので、以下のような更新式でできる。
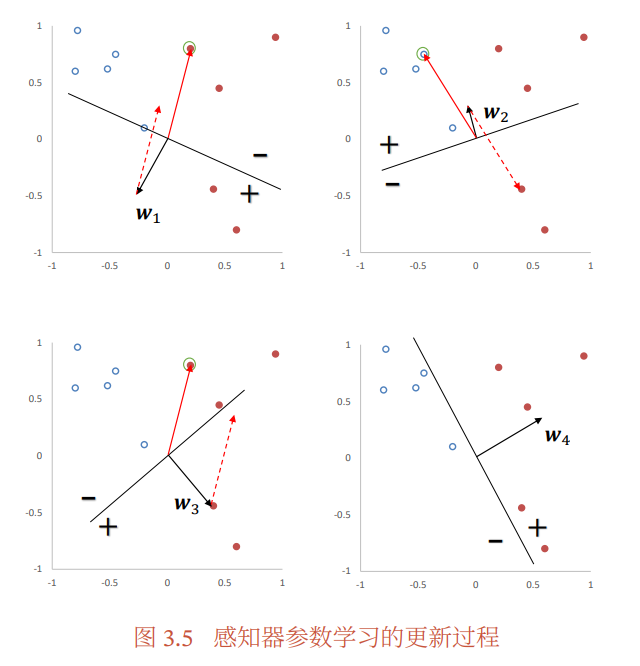
データが有限で、線形で可分なのであればパーセプトロンは必ず有限回の更新を経て収束することが保証されている。
ただ欠点としては、可分でなければ収束は永遠にしないし、過学習するし、更新する順序によって最終的に得る分類超平面も異なってくる。
パラメタ平均式パーセプトロン
各種を防ぐために過去のパラメタを保存して、それぞれに重みを設定し、最終的な識別結果は重み付きの各識別器による投票で判定することで、ロアスト性を高めることができる。しかし、パラメタ保存するのがめんどくさい。=Voted Perceptron
毎回保存するのがめんどくさいときは、最近のものを重視する指数平均、単純に平均を取る無印の平均などで対処できる。
多クラス分類パーセプトロンへの拡張
全てのラベルの集合をとする。この時、多クラス分類の式は、外積演算子を用いると以下のようになる。はone-hotである前提。
外積を取る事によって、カテゴリで次元の特徴量であることから、次元のベクトルとなる。具体的には以下のように、指定の部分の行だけ値が入ってそれ以外が0になっている。
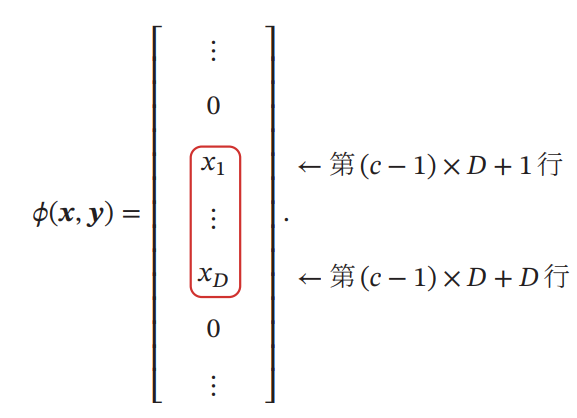
Support Vector Machine(支持向量机)
マージンとは、各点から識別器の超平面までの最短距離だと定義する。
より大きいマージンだとより良い分類ができるのでそれが望ましい。
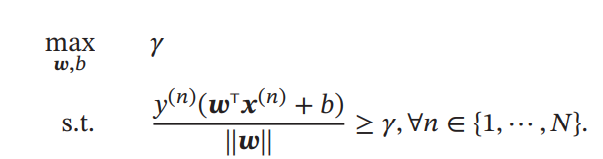
と制限しても表現力は変わらないので、以下の最適化問題となる。
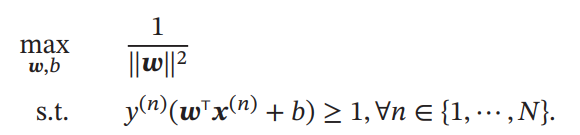
s.t.の部分で=1となるようなすべてのサンプルの位置ベクトルは、サポートベクトルという。
パラメタの更新
凸最適化問題に書き換えると以下の通り。
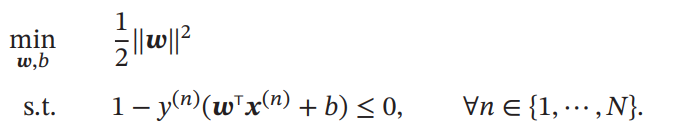
あとは、ラグランジュの未定乗数法などで解けばよい。サボります。
あとはカーネル法を使えばSVMの表現力を上げることができる。
また、分離不可能な場合では、最適化問題をペナルティの係数を導入して以下のようにあらわす。

