前回はこちら。📄 (講義ノート)統計的機械学習第5回
(講義ノート)統計的機械学習第5回
📄 (講義ノート)統計的機械学習第3,4回 でRademacher複雑度を導入することで、理想誤差を0にできる仮説、そして有限仮説の集合ではない場合でも解析できるとしていた。しかし、それは損失関数についてのRademacher複雑度であり、仮説についてのRademacher複雑度の変換Rn(L01)=21Rn(H)がわかった。
(講義ノート)統計的機械学習第3,4回 でRademacher複雑度を導入することで、理想誤差を0にできる仮説、そして有限仮説の集合ではない場合でも解析できるとしていた。しかし、それは損失関数についてのRademacher複雑度であり、仮説についてのRademacher複雑度の変換Rn(L01)=21Rn(H)がわかった。
また、有限仮説の集合であれば、Massartの有限仮説の補題を用いることによって、Hoeffdingの不等式で得た結果と同じ結果が得られるとわかった。Massartの有限仮説の補題自体は非常に有益な補題。
経験損失と期待損失の解析
今まででは、1−δ以上の確率で
L(h^)−L(h∗)≤4Rn(H)+2(b−a)2nlog(2/δ) で成り立つという結果がわかった(McDirmidの不等式など)。これは理想のLについて、経験的に決めたh^と理想の仮説h∗の差であった。しかし、経験的に決めた仮説の、経験的な損失Ln(h^)とL(h^)との差も重要である。
1−δ以上の確率で、以下の式が成り立つ。
L(h^)−L^n(h^)≤2Rn(L)+(b−a)2nlog(1/δ) 証明
L(h^)−L^n(h^)≤suph∈H{L(h)−L^n(h)} まず、📄 (講義ノート)統計的機械学習第3,4回 でのMcDiarmidの不等式+Rademacher複雑度で、L(h)−L^n(h)は上限で評価すると、1−δ以上の確率で以下が成立していた。(これの符号を逆転させたものの上限と両方していった 第3,4回のノートでは1−δ/2以上の確率としていたので、log(2/δ)となっていた)
(講義ノート)統計的機械学習第3,4回 でのMcDiarmidの不等式+Rademacher複雑度で、L(h)−L^n(h)は上限で評価すると、1−δ以上の確率で以下が成立していた。(これの符号を逆転させたものの上限と両方していった 第3,4回のノートでは1−δ/2以上の確率としていたので、log(2/δ)となっていた)
G^n=suph∈HL(h^)−L^n(h^)G^n≤E[G^n]+(b−a)2nlog1/δ よって、これで右辺を抑えることができるので示せた。
経験Rademacher複雑度
今までは損失関数のクラス、仮説のクラスについてのRademacher複雑度について論じてきたが、データは理想的な分布からえるという仮定だった。
これを経験的なデータから計算する、ということはもちろんできる。以下のように期待値はデータ分布ではなくなり、Rademacher変数のみの期待値となる。
RSn(F)=Eσ[supf∈Fn1∑i=1nσif(Zi)] この経験Rademacher複雑度について、以下の式が成り立つ。2つのデータ集合Sn,Sn′があり、1つだけデータZj→Zj′と変わっていて違うとする。仮説集合はF:f:Z→[a,b]である。
∣R^Sn(F)−R^Sn′(F)∣≤nb−a つまり、データが違くとも、仮説に対するRademacher複雑度は1つ変えるだけなら- 高々(b−a)/nしかずれない。
証明
一般的に以下が成り立つ。別々にsupとったものの差より、一緒に動かしたsupのほうが大きい。
Rademacher複雑度を展開すると、以下のようになる。上の式を利用してだいぶ打ち消すことができ、最終的にはfの取りうる値の最大の差で抑えることができる。
R^Sn(F)−R^Sn′(F)=E[supf∈Fn1∑i=1nσif(Zi)]−E[supf∈Fn1∑i=jσif(Zi)+σjf(Zj′)]≤E[supf∈Fn1(σif(Zj)−σf(Zj′))]≤nb−a これによって、経験Rademacher複雑度のズレを評価できたので、McDiarmidの不等式を使っていく。
1−δ以上の確率で、以下が成り立つ。
∣Rn(F)−ESn[R^Sn]∣≤(b−a)2nlog(2/δ) つまり、経験Rademacher複雑度は理想と比べてのズレを評価することができた。今までは理想的データ分布に基づくズレについて議論してきたので、これらを統合できるようになる。
なお、理想的なデータ分布を用いたRademacher複雑度の評価をしたのは、McDiarmidの不等式を用いて示せた以下の式である。1−δ以上の確率で成り立つ。
L(h^)−L(h∗)≤4Rn(L)+(b−a)n2log2/δ 損失関数の集合と仮説集合の関係
Rademacher複雑度のルールから、損失関数集合と仮説集合の関係性がわからないと、Rademacher複雑度の評価は損失関数の集合の評価で終わってしまう。
ここで、有名な各モデルについての分析していきたい。
そこで、重要なLedoux Talagrandの補題というのについて説明する。
Ledoux Talagrandの補題
界隈でよく言われる、Talagrandの補題である。
ϕ:R→Rを、リプシッツ連続な関数でリプシッツ定数がLϕであるとする。つまり、
∣ϕ(x)−ϕ(y)∣≤Lϕ∣x−y∣ そして、F⊂Rnであるとき、以下が成り立つ。
E[supf∈Fn1∑i=1nσiϕ(fi)]≤LϕE[supf∈Fn1∑i=1nσifi] つまり、傾きの上界を抑えられる関数の場合、その傾きの上界=リプシッツ定数Lϕとすることで、外に出すことで抑えることができる。
証明
以下のことをi=1,2,⋯と繰り返せばよい。
まず1つだけ出してから、Rademacher変数は21(+1)⋅A+21(−1)⋅Bと分解できることを利用する。このように出すことができるが、別々のsupに分解していることについては、=ではなく≤では??
そしてくくりだした部分について、仮定を用いることができ、最後にf,f′は対称性を持っているのでsupをどうせとっているので、絶対値を外すこともできる。これをずっと繰り返していくことで、Talagrandの補題を証明することができる。
L2正則化線形モデルの仮説空間
入力xに対して、ラベルy=+1.−1とすると、損失関数に入れるのはだいたいxと予測した結果。∣∣x∣∣22=C22という二次ノルムの上界で抑えられるとする。
そして、仮説はh(x)=wTxであるとする。この時、重みのノルムの上界は∣∣w∣∣22≤B2だと、同様に二次ノルムで抑えられるとする。この制限は実質的にはL2正則化項を損失関数に加えることに相当する。つまり、ここで仮説空間は線形モデルであるうえ、重みのL2ノルムに上界を設けたものである。
、Rademacher複雑度は以下のように抑えられる。
Rn(H2)≤nB2C2 証明
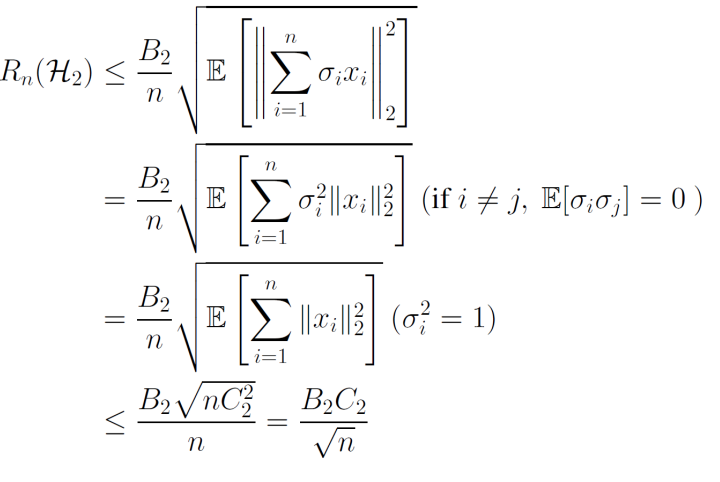
愚直に展開したあと、内積の形であるので、σiをデータxiにまとめて、そこからコーシー・シュワルツの不等式を用いることで∣∣w∣∣2と∣∣∑i=1nσixi∣∣2に分割できる。これでうまくwを出す形になった。目標はsupよりも外に出して、すでに分かっている制約∣∣w∣∣22≤B2を適用させること。
次に、∣∣w∣∣2は、上界をとれば外にB2として出すことができる。中に残った部分に関してはまた評価を進める。
中にあるのは一次の形なので、2乗の和のルートということになる。ここでほしいのは、Rademacher変数の線形和についての期待値(ルートは評価するうえで邪魔なので出したい)
ここで、ルートは上に凸の関数なので、Jensenの不等式を用いることでうまく出すことができるのだ。
期待値の中は単純に2乗であるが、Rademacher変数入りのものを二乗するときは、Rademacher変数がそれぞれ独立になることに留意。つまり、σi,σjについての期待値になるということ。
そして、E[σiσj]=0,i=jが成り立つ。i=jならば1となる。これを利用すると、2乗の項しか残らないし、しっかり∣∣x∣∣22≤C22を利用することができ、評価することができた。
これによって、重みについてL1ノルムについての評価なので、L1正則化?
L1正則化線形モデルの仮説空間
データxについて、最大の成分が有界である。つまり、∣∣x∣∣∞≤C∞となる
同様に、h(x)=wTxを使うとする。
重みについて、L1ノルムが上界であるとき、∣∣w∣∣1≤B1である。
この時、Rademacher複雑度は、以下のように抑えられる。
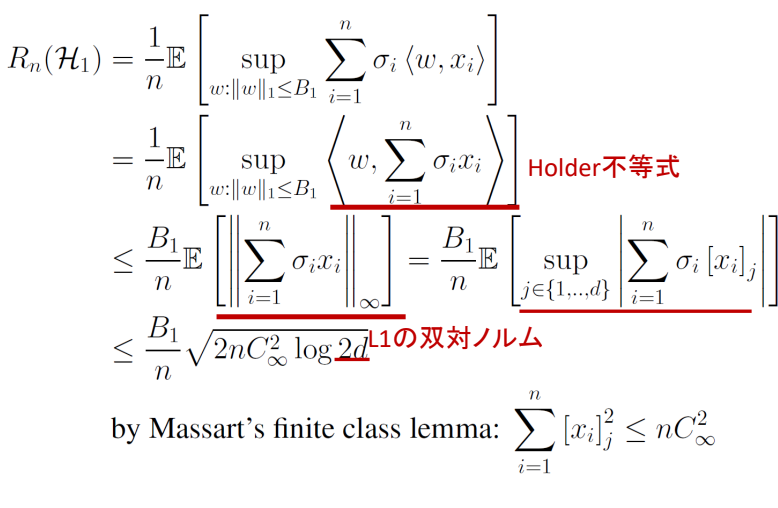
Rn(H1)≤B1C∞n2logd L∞ノルムにはL1ノルムを使っているのか
なお、なぜL∞ノルムを使うのかというと双対ノルムだから、以下のように双対ノルム∣∣⋅∣∣∗は定義されている。対象のベクトルに対して、今のノルムで1以下のベクトルとの内積の最大値である。
∣∣x∣∣∗=sup∣∣y∣∣≤1<x,y> ここで、xがL∞ノルムで制約されている(最大の成分が有界)とき、supを満たすのは同じ向きを向いているL∞ノルムが1以下(最大成分が1)のベクトルであり、これは(1,1,⋯)となる。よって、この内積を計算すると、実質すべてのxの成分を足し合わせるので、∣∣⋅∣∣∗はL1ノルムである。
証明
📄 (講義ノート)統計的機械学習第5回 でやったMassartの有限仮説の補題を使う(かたちがいかにもそれ)
(講義ノート)統計的機械学習第5回 でやったMassartの有限仮説の補題を使う(かたちがいかにもそれ)
A∈Rnの有限集合とする。
∃M≥0,supa∈A∑i=1nai2≤M2Eσ[supa∈An1∑i=1nσiai]≤n2M2log∣A∣ Racdemacher複雑度のsupとして、線形モデルかつ重みベクトルがL1ノルムで制限されているという仮説集合を考えている。
Holderの不等式を使う。L2ノルムの場合ここでコーシー・シュワルツの不等式を使っていた。Holderの不等式では以下のようになっていた。
任意の数列{ai},{bi}について、p>1,1/p+1/q=1を満たすqについて以下が成り立つ。等号成立条件はp=q=2であり、通常の我々が見る内積でのコーシー・シュワルツの不等式にあたる。
∑i=1n∣aibi∣≤(∑i=1n∣ai∣p)1/p(∑i=1n∣bi∣q)1/q つまり、LpノルムとLqノルムの積は普通の内積以上ということ。
そして、これを満たすp,qはお互いに双対ノルムの関係にある。
実際に、p=1,q=∞でも成り立つ。
このHolderの不等式について、二行目は内積なのでwについてのL1ノルムと、σixiについてのL∞ノルムについて分けられて、その積以下と抑えることができる。
そして、wのL1ノルムのほうについて明らかに最大値がB1であることから、出すことができてて期待値の中でL∞ノルムが残る。
さて、L∞については最大の成分を取り出すので、supで一番最大の値をとるj∈{1,⋯,d}を考える。そして、その中のΣではRademacher変数を掛け合わせているので、ちょうどMassartの有限仮説の補題を使える形である(仮定により、各成分xiは有界)。
よって、使うことによって(示した形の左辺の1/nは右辺に移すせばnになる)
n2M2log∣A∣=2C∞2nlog2d ∣A∣=2dとなっていて、これはxiは実質最大を取ると考えるなら、d次元なら各成分+B1,−B1と2つあるので、2d個の有限集合である。
L1正則化とL2正則化の違い
L2正則化はデータも、係数も2乗ノルムで制限されている。L1正則化はデータは成分の最大値が、係数は1乗ノルムが制限されている。
実をいうと上の式もdを持っている。同じデータに対して、∣∣x∣∣∞≤C∞と抑えられるとき、データのL2ノルムは∣∣x∣∣2=C2=dC∞となる(各成分が最大値をとってd個足し合わせる感じ)
このように、C2はdを含んでいる、というわけである。
L1正則化の問題点
L1正則化はsparse化することができる。📄 NNDL 第7章 Networkの最適化と正則化
NNDL 第7章 Networkの最適化と正則化
説明変数のほうがデータ数よりも多い(over parameterized)の時は、実質どれを選ぶかを決定できず、選ばれたor選ばれなかった特徴量に解釈性があるわけではない。
また、相関が高い説明変数の集合があるとき、そこから1つしか変数しか選ばれない(良くも悪くも)
確かに選んだものの説明はできるが、選んだものが本当に最重要かはわからない。あくまで仮説の生成。
(講義ノート)統計的機械学習第5回
(講義ノート)統計的機械学習第3,4回 でRademacher複雑度を導入することで、理想誤差を0にできる仮説、そして有限仮説の集合ではない場合でも解析できるとしていた。しかし、それは損失関数についてのRademacher複雑度であり、仮説についてのRademacher複雑度の変換がわかった。
(講義ノート)統計的機械学習第3,4回 でのMcDiarmidの不等式+Rademacher複雑度で、は上限で評価すると、以上の確率で以下が成立していた。(これの符号を逆転させたものの上限と両方していった 第3,4回のノートでは以上の確率としていたので、となっていた)

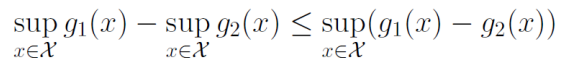
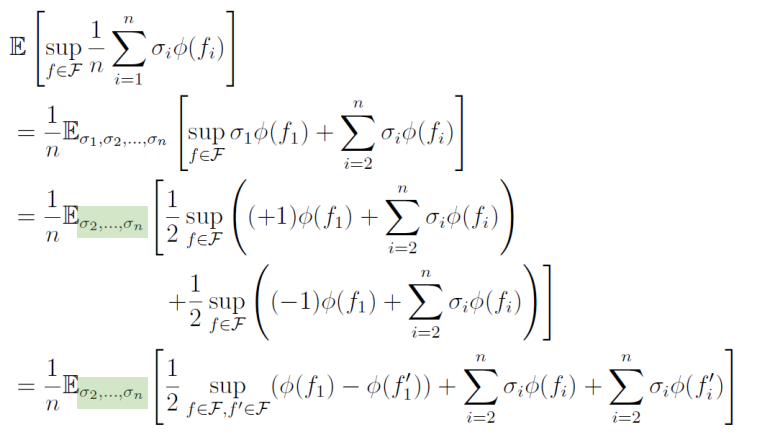
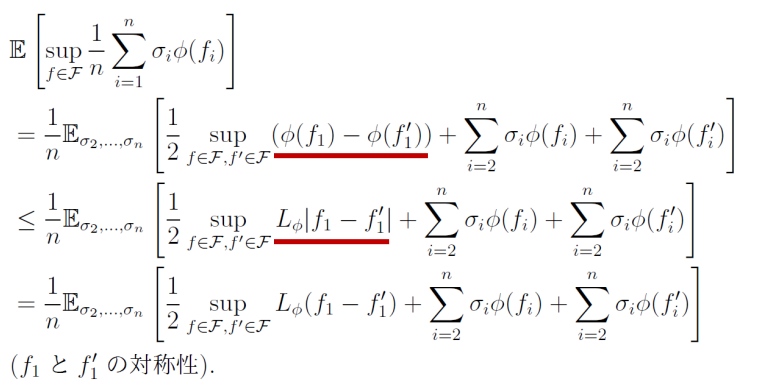

(講義ノート)統計的機械学習第5回 でやったMassartの有限仮説の補題を使う(かたちがいかにもそれ)

NNDL 第7章 Networkの最適化と正則化
