Sen(Qian)’s Memo

前回はこちら。📄(講義ノート)統計的機械学習第11回 。内容は位相空間についての説明だった。

線形代数に収束の概念を導入するため、位相を備えた線形空間を考えたい。有限次元だと、フーリエ級数みたいなのを取り扱うことができない。

ベクトルの長さに対応するノルムを用いるのが数学的にも扱いやすい。

線形空間の性質は以下のようなもの。

では、無限次元が存在する関数($f(x)$が$x$次元目の成分をとると考えて)というものについて、ノルムを考えられないだろうか？

以下のように一般的に定められている。普通は$\sup$をとる=L∞ノルムとして考える。

連続関数や$X \to \mathbb{R}$となる関数で、$X$の上で可積分の関数は線形空間であり、定義として

満たすのは三角不等式、同次性/斉次性。

$u=0 \Leftrightarrow ||u||=0$については成り立たず、$\Rightarrow$は成り立つが逆は成り立たない。

距離空間$(X,d)$だとする。$K \subseteq X$である。$K$が有界ということは以下が成り立つ。

$K$のすべての元$a$と、同じ集合に含まれるほかの元の距離が高々$M$で抑えられる。

まずは$\exist a$で定義できるが、これを$\forall$に拡張するときは三角不等式を使い、絶対に不変の$a$だとしたら高々$M+M$で右辺を抑えられるってこと。

距離空間においては、点列コンパクト性とコンパクト性は違うが、これは距離空間に限る話。

$K \subseteq X$が点列コンパクトであるとは、$K$が位相(開集合の集合族)であるが、に含まれる任意の点列$(x_n)_{n \in \mathbb{N}}$に対して、$K$の中の点に収束する部分列が存在することである。

位相空間論においての、一般的なコンパクト性とは「有限の大きさを持つ」という意味でしかない。位相空間$(X,A)$がコンパクトであるとは、$\bigcup_{i=1}^m U_i \supseteq X$となるような被覆$U$があるということ($X$に含まれていないような元を含む集合もあり得る)。そのうえで、どんな$\{ U_i \}_{i=1}^m$でもその中にある有限個の要素からなる集合$\bigcup_{j} U_j \supseteq X$になれるということ。

有限個の開集合の和で表現できる=空間は有限の大きさを持つ、有限個の開集合の和集合で表せるということ。

例えば、$\mathbb{Q}$有理数とかはコンパクトではない。$U_i$に実数、複素数が入ってしまうのならば、ちょうど有理数の集合$\mathbb{Q}$にはなりえないという感じである。

これについて、点列コンパクト性とコンパクト性は明確なカウンターパートがあるわけではなく、非自明な証明でつながっている。

閉区間$[a,b]$はコンパクト性を持つ。なぜなら、これを満たす有限個の開区間$(0,1)(0.5,1.5)(-1,3)$などのように選べばそれの和集合で確かに当然ながら被覆できる。

$(-\infty,3]$とかは無限が入っている以上、有限個の開集合の和集合で表せないのでコンパクトではない。つまり$\mathbb{R}$を両端にとる区間はコンパクトではない。

有限次元空間では、「部分空間がコンパクト」は「有界閉集合」であることの必要十分である。だが、無限次元空間では「部分空間がコンパクト」→「有界閉集合」しか成り立たないことに注意！

コンパクト集合$K$上の連続関数$f$は、

• 最大値、最小値を持つ → 最適化問題として定式化できる。
• 一様連続 →$K$上での近さで$f$の近さを議論できる。
  • $(C(K), || \cdot ||_\infty)$という距離空間は完備である=コーシー列があるなら収束するという完備性を持つような空間。

ノルム空間を無限次元の関数とかでも定義できたので、いよいよ線形代数の線形空間を考える。有限次元だけにとどまらない、無限次元を考えられるものを！

有限次元では行列にあたるもの。

$X,Y$を$\mathbb{R}$のノルム線形空間だとする。写像$T:X \to Y$が線形作用素であるということは、以下のように線形性を持つということ。

ここで面白いのは、$X,Y$はノルム線形空間であるが、線形作用素自体も線形空間でもある。

上の方は、$x$を近づけるとき、適用先も0へ近づくならば、連続である。

下の方はすべての$x \in X$に適用させても、ちゃんとスカラーの$M$で抑えられるよってこと。

ようわからん。

線形空間(例えば$\mathbb{R}$上の線形空間の$\mathbb{R}^n$)から、その係数体(線形空間を構成する各次元のもの。先ほどの例だと$\mathbb{R}$)。線形空間で表されるものを多項式と考えて、それの係数を得るみたいなイメージ。無限次元とかだと、ヒルベルト空間なら関数の内積とか。

汎関数$l: X \to \mathbb{R}$に関して、三角不等式と斉次性は満たすのならば劣線形汎関数である(半ノルムみたいだよね)

なにかを測る。$\mathbb{R}$体上のノルム線形空間$X$の部分空間$K$が凸集合であるとする。0を内点として含むとする。

ゲージ汎関数は以下のもの。$x$に$1/a$をしても$K$に含まれるとき、そうなる一番小さい$a$ということ。

例えば、$x\in K$ならば、自明に$a=1$は成り立つ。$2x$が与えられたとき、$K$には高々$x$までしか入っていない場合は$a=2$をどうしてもしないといけない。この時、ゲージ汎関数は2を返す。

つまり、許される区間$K$に与えられた値を押し込むのに、一番最低限で割るいくつが必要か？ってこと。

この関数は実は劣化法性(三角不等式が成り立つ)、同次性、非負性を持つので、$X$上の半ノルムである。

うれしい性質として、$p_K(x) < 1 \Leftrightarrow x \in K^\circ$。ゲージ関数が1未満なら内点である。

このように、各元についてそれぞれの和/差を$|A| \times |B|$通りエミュレートしたい。

凸集合$A,B$のミンコフスキー和/差は同じく凸集合になる。

• 閉集合とは、開集合の補集合
• コンパクト集合とは、一般的には有限個の開集合の和で被覆できる集合。
  • 距離空間の場合、集合内の任意の元に収束する点列があるということ。

$X$を$\mathbb{R}$体上のノルム線形空間とする。

$A \subseteq X, B \subseteq X$を$X$の凸な空ではない部分集合とする。$A$はコンパクト集合で、$B$は閉集合。

閉集合とコンパクト集合のミンコフスキー和と差は閉集合である。

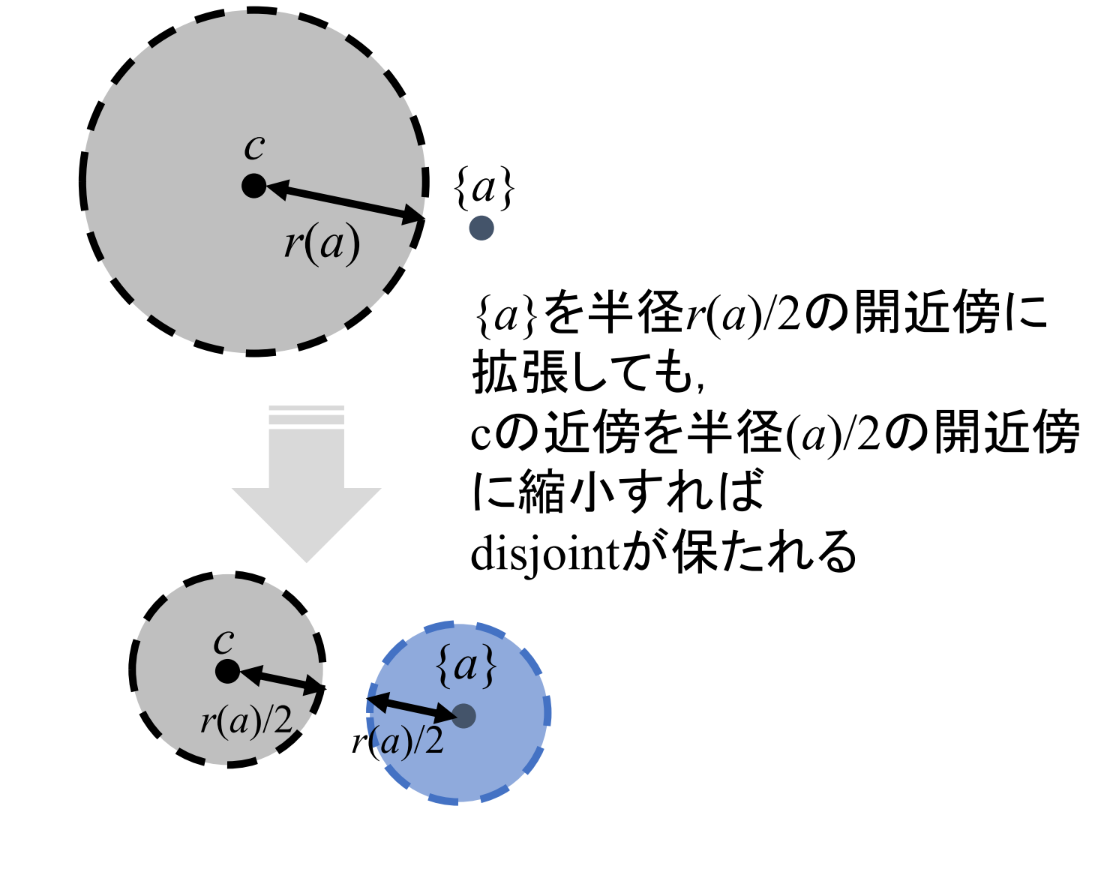
開近傍について、半径$r(a)$で$\{a\}$を含んでいないなら、半径$r(a)/2$の開近傍と、$a$から半径$r(a)/2$の開近傍も当然交わらない。

ミンコフスキー和は閉集合の証明なので、内部の点が触点であればよい。触点の集合は閉包であり、閉包は閉集合。ここでは触点ではない、から考えている。

ミンコフスキー和の定義から、$c＝a+b$なので、$c-a \notin B$であるとも言える。

次に$B$が閉集合であることを愚直に書き直し、含まれないものは触点ではないってこと。

ようわからん。いろいろ証明は。