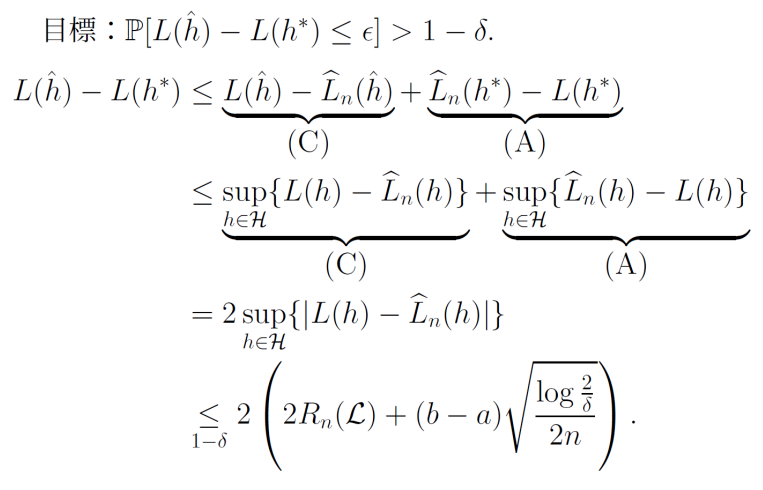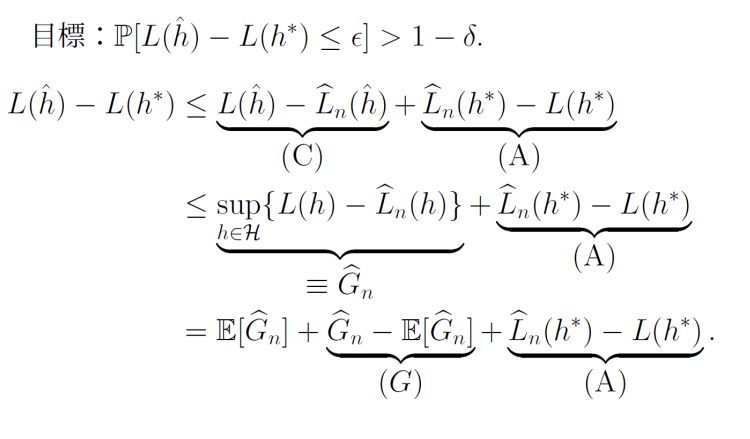前回はこちら。📄 (講義ノート)統計的機械学習第3,4回
(講義ノート)統計的機械学習第3,4回
前回はL(h∗)=0、仮説集合が無限と条件をどんどん緩くしたうえで、誤差上界の評価の手法について紹介された。L(h∗)=0の時はHoeffdingの不等式で分布の裾で評価した。仮説集合が無限の時は、McDiarmidの不等式でG^n(h)=Ln(h^)−L(h∗)と評価した。
Rademacher複雑度による仮説集合の汎化誤差解析
損失関数が取る値が[a,b]の時、汎化誤差の上界は以下のようになることがわかった。
L(h^)−L(h∗)≤ϵ=4Rn(L)+(b−a)n2log(2/δ) Rn(L)は損失関数の集合についての評価である。ただ、損失関数じゃなくて仮説集合のRademacher複雑度にやはり評価したい。
主張
- 仮説関数はh:X→{+1,−1}であり、これの集合をHとする。
- 損失関数は01損失であり、l((x,y),h)=1[h(x)=y]となる。これの集合をL01とする。
この時、以下の式が成り立つ。
Rn(L01)=21Rn(H) このような変換関係が成り立つ。
証明
指示関数1[h(x)=y]=21(1−yh(x))と書き換えることができる(よくある)。
ED[Eσ[supl∈L01n1∑i=1nσi⋅21(1−yih(xi))]]=21ED[Eσ[suph∈Hn1∑i=1nσi⋅(1−yih(xi))]]=21ED[Eσ[suph∈Hn1∑i=1nσi+n1∑i=1n−σiyih(xi)]]=21ED[Eσ[suph∈Hn1∑i=1n−σiyih(xi)]]=21Rn(H) 3行目から4行目の式変形では、Rademacher変数σiの和はベルヌーイ分布で半々で1か-1をとることから、実は0であること言うことを利用して消した。その結果、Rn(L01)をRn(H)で評価する計算ができた。
有限集合のRademacher複雑度
有限仮説集合Hがあるとする。この時、以下のMassartの有限仮説の補題によって、以下のものが成り立つ。
Rn(H)≤n2log∣H∣ ここで、Massartの有限仮説の補題は以下のとおりである。A∈Rnの有限集合とする。
∃M≥0,supa∈A∑i=1nai2≤M2Eσ[supa∈An1∑i=1nσiai]≤n2M2log∣A∣ 証明
x1,⋯,xnのデータがあるとする。それらにすべてとある有限仮説集合の元h∈Hで予測をする。それをAnとする。
An={h∈H,(h(x1),⋯,h(xn))} 有限仮説集合で、有限個のデータなので、Anは有限集合であり、{−1,+1}nの部分集合でもある。以下のように各Anの元のベクトルの成分の2乗和の上限は高々nである。
supa∈An∑i=1nh(xi)2=suph∈H∑i=1nh(xi)2=n ここで、Massartの有限仮説の補題と、An⊂H(複数通りの仮説hが結果的に同じAnの元を生成することがある)によって、以下の式変形が成り立つ。
- ここではh(xi)2は上限M2=nが存在することで、Massartの有限仮説補題を利用。
- 中のRademacher複雑度の部分の期待値をMassartの有限仮説で抑えた。
- 期待値を外してもいいので、結果を得る。
結果として、有限仮説集合HのRademacher複雑度は、以下のように評価できる。
Rn(H)≤n2log∣H∣ そもそも有限仮説集合の場合、誤差上界の評価をするときはHoeffdingの不等式でよく(📄 (講義ノート)統計的機械学習第3,4回 )そこでは、上界は以下のようになっていた。
(講義ノート)統計的機械学習第3,4回 )そこでは、上界は以下のようになっていた。
n2(log∣H∣+log(2/δ)) このルートの中の左辺がRademacher複雑度にあたるもの?であるが、見事なまでに一致している。
Massartの有限仮説の補題
A∈Rnの有限集合とする。
∃M≥0,supa∈A∑i=1nai2≤M2Eσ[supa∈An1∑i=1nσiai]≤n2M2log∣A∣ 証明
まず、一般的に有限集合Xにおいて、f(x∗)=supx∈Xf(x)をとる。この時、指数関数は単調増加関数なので、以下の式はもちろん成り立つ。このようにsupをいじることで、Rademacher複雑度をどうにかできる。
exp(f(x∗))=supx∈Xexp(f(x))f(x∗)=log(supx∈Xexp(f(x))) 証明の本体を説明する。
まず、任意のλ>0を考えて、それを示したい式の左辺になぜか乗じる。
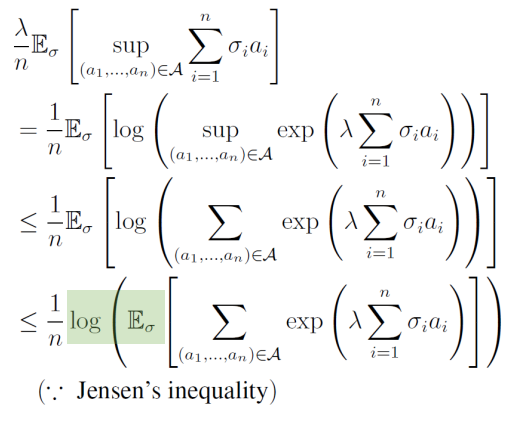
- まず、先ほどの一般的なsupの変形を利用する。supA=log(sup(exp))という感じ。
- 2行目から3行目はsupを総和で上から押さえている。よくある変形テクらしい。
- 3行目から4行目は、Jensenの不等式を使う。logは凸関数であるので、Jensenの不等式により凸関数h=logは以下が成り立つ。
- つまり、凸関数に代入した後の和(や期待値)より、和(や期待値)をとった後凸関数に代入したほうが等しいか大きい。
h(E[X])≤E[h(x)] さらに式変形を重ねていく。expの中の総和を外に出して∏にすることができ、Eσもa∈Aの総和の中に入れていい。
ここで、指数関数の中の総和を外に出したうえ、Eσiを中に持ってきたことによって、独立した各変数の期待値の積という形にすることができ、操作しやすい。これもよくやる変形。
=n1log(∑a∈A∏i=1nEσi[exp((λσiai))]) ここからもっと変形していく。ここでやりたいのは、Rademacher変数の期待値の部分を上から押さえることで消滅させたい。こういう時は、Rademacher変数による影響を高々で抑えていくことができる。
=n1log(∑a∈A∏i=1n21exp(σiai)+21exp(−σiai))≤n1log(∑a∈A∏i=1nexp(2λ2ai2)) ここでは、以下の2点を利用した。
- Rademacher変数を分解した。半々の確率で+1や-1をとるというのを愚直に分解すると、簡単な目的関数ならそれだけですっきりする。
- 指数関数については、以下の特性がある。
2exp(x)+exp(−x)≤exp(2x2) 最後の仕上げの証明の式変形をする。
- Massartの有限仮説の仮説を用いることで、上限があるということ。これを第2から第3行目への式変形で使用した。
- A自身も有限集合であるという仮説であるので、元の数で抑えることができる。
ここまでで、大体Massartの有限仮説の証明は終わる(おおむね形が出てきた)。しかしなぜλが必要なのだろうか?最初にλを付け加えておくと、exp(x2/2)となる部分でλ2を作れて、最終的に相加相乗平均のかたちにできるからだ。
両辺をλで割ると、以下のようになる。
相加相乗平均を用いて上限を低く抑えることを考える。書いてあるように、λ=2M2log∣A∣とすれば、上限を低く抑えて最終的に、2M2log∣A∣/nとなる。
気持ち: 非常に技巧的な証明ですね!
汎化誤差
やりたいことは、L(h^)−L(h∗)を、1−δ以上の確率でϵに抑えたいということ。
これについていろいろ今まで考えてきた 📄 (講義ノート)統計的機械学習第2回 📄
(講義ノート)統計的機械学習第2回 📄 (講義ノート)統計的機械学習第3,4回 が、別解もあるので軽く紹介していく。
(講義ノート)統計的機械学習第3,4回 が、別解もあるので軽く紹介していく。
L(h^)−L(h∗)≤{L(h^)−L^n(h^)}+{L^n(h∗)−L(h∗)} - 一項目の{L(h^)−L^n(h^)}は、h^は訓練データに依存するため、L^n(h^)は独立な損失関数の和とならず、確率的なふるまいを分析するのは難しい。
- {L^n(h∗)−L(h∗)}はh∗は訓練データから独立しているので、分析は容易である。
- 大数の弱法則で0へ収束するとわかる。
- 中心極限定理で、収束速度はO(1/n)であるともわかる。
汎化誤差の導出で今までは、指数関数、Hoeffdingの不等式、McDiarmidの不等式で評価していた。これらについて別解を考えてみる。
McDiarmidの不等式で全部評価
同じ仮説に対して、違う損失関数のものは、suphで抑えられる。それを使い、McDiarmidの不等式に代入して終わり。
G^nを作り出す。
h^は嫌なので、減らしていきたい。実はその部分はG^nであったので、変形していく。期待値からの外れをわざわざ作り出して、
- (A)は普通に抑えられる。
- (G)は中心極限定理で評価できる。まさにMcDiarmidの不等式で評価する。
- E[G^n]をどう評価するか?ここは前に議論した通りRademacher複雑度となる。
(講義ノート)統計的機械学習第3,4回
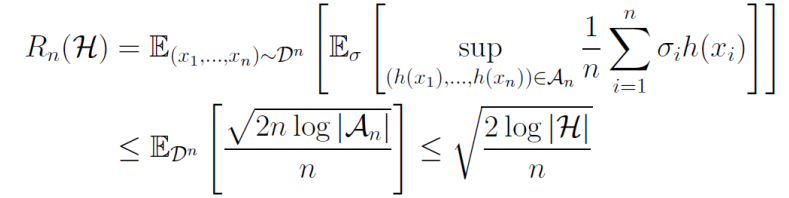
(講義ノート)統計的機械学習第3,4回 )そこでは、上界は以下のようになっていた。
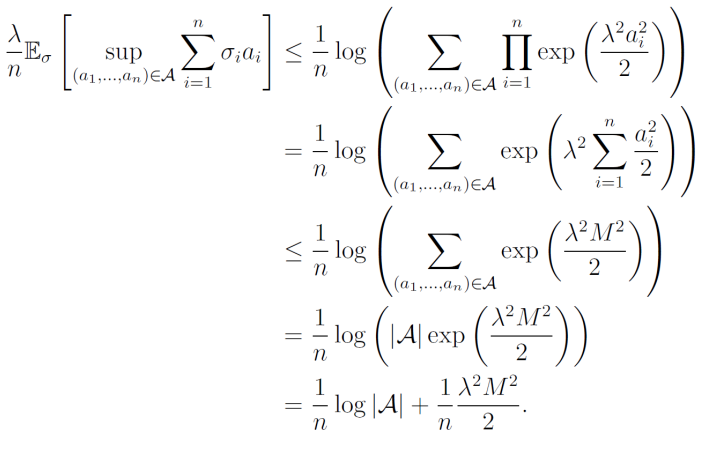
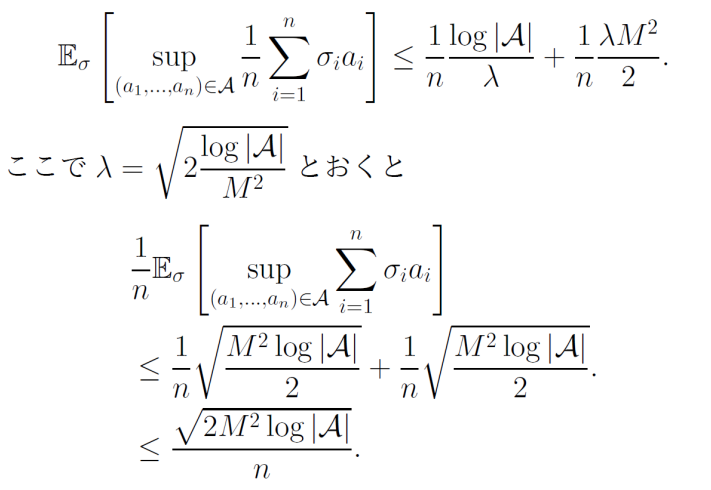
(講義ノート)統計的機械学習第2回 📄
(講義ノート)統計的機械学習第3,4回 が、別解もあるので軽く紹介していく。