前回はこちら。📄 (講義ノート)統計的機械学習第2回
(講義ノート)統計的機械学習第2回
前回は真の損失関数Lで、有限の訓練データについてh^が最適であったとき、以下のような式が成り立っていた。h^∈argminh∈HL^n(h)つまり経験損失を最小化させるものをh^だとすると、少なくとも1−δ以上の確率で
L(h^)≤n1(log∣H∣+log(1/δ)) ただし、ここでは、最適な∃h∗,L(h∗)=0が存在しない場合を考える。
∀h∗,L(h∗)=0であるときの上限
モデルや仮説の仮定
非常に基礎的なモデルから解析していく。
- X⊂Rdが学習データ
- Y={+1,−1}がラベルである二値分類。
- 損失関数はすべて01損失。つまり、損失関数というのは条件を満たさない確率そのものである。
仮説は2つの仮定の下で行う。
示したいもの
この仮定の下で、h^∈argminh∈HL^n(h)とする。この時、少なくとも1−δ以上の確率で以下の式が成り立つ。
L(h^)−L(h∗)≤n2(log∣H∣+log(2/δ)) 理想損失を0にするような識別器が存在しないとき、1/n→2/nとなり、1/δ→2/δとなっている。
証明
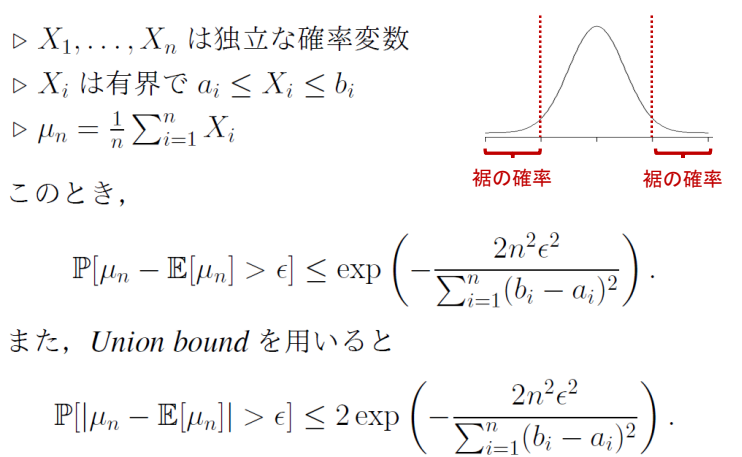
Hoeffding’s Inequality
📄 (講義ノート)乱択アルゴリズム第2回 を参考
(講義ノート)乱択アルゴリズム第2回 を参考
各確率変数が独立で、それぞれ上と下にとる値が定まっている=有界である。
ここで、経験平均と平均の期待値がϵより大きくずれるのは、上限で評価できるというもの。
下の式は、両側のすそを考慮したものである。
証明の方針
今まで通り、L(h^)−L(h∗)ではなく、すべてのhについての上限suph∈H∣L(h)−L^n(h)∣を考える。あるh∈Hで成り立つので、Union Boundで示していく感じ。
∃hで評価する
あるhを固定すると、L^n(h)はn個の独立な損失関数l((xi,yi),h)の平均であり、LもL^nも確率と同等なので、[0,1]の値をとって有界である。なので、Hoeffdingの不等式を使うことができる。よって、以下のようになる。
Pr[∣L^n(h)−L(h)∣>ϵ]≤2exp(−∑i=1n122n2ϵ2)=2exp(−2nϵ2) そこから、h∈Hで仮説集合は有限サイズだという仮説なので、以下のようにUniform Convergenceで、集合全部のサイズで抑える形で確率の和というかたちで変形できる。
Pr[suph∈H∣L^n(h)−L(h)∣>2ϵ]=Pr[∃h∈H,∣L^n(h)−L(h)∣>2ϵ]∑h∈HPr[h∈H∣L^n(h)−L(h)∣>2ϵ]≤∣H∣⋅2exp(−2n2(2ϵ)2)=∣H∣⋅2exp(−2nϵ2) ここで、以下のようにδを置くと、与えられたものを得る。
∣H∣⋅2exp(−2nϵ2)=δϵ=n2(log∣H∣+log(2/δ)) ここで、前回の授業のように、L(h^)−L(h∗)はsuph∈H∣L^n(h)−L(h)∣で一様収束性を使って評価することができることを使う。
Pr[L(h^)−L(h∗)>ϵ]≤Pr[suph∈H∣L(h)−L^n(h)∣>2ϵ] ここで不等式を逆にすることで、以下のようになる。先ほど定義したδを使う。
Pr[L(h^)−L(h∗)≤ϵ]>Pr[suph∈H∣L(h)−L^n(h)∣≤2ϵ]>1−δ なので、左辺と右辺の評価からして、少なくとも1−δ以上の確率で、以下が成り立つ。
L(h^)−L(h∗)≤n2(log∣H∣+log(2/δ)) 証明したかったのはL(h^)−L(h∗)の差による不等式だが、不等式をそのまま使うと評価できるのはLn(h^)−L(h∗)のかたちである。なので最初からϵ/2で計算していて、その後変換をした。
大筋
- L(h^)−L(h∗)はsuph∈H∣L^n(h)−L(h)∣で一様収束性を使って評価を変える。
- supは有限仮説集合であることを利用して、Uniform Convergenceを使って抑える。
- Uniform Convergenceの合算する各要素のPr[∣L^n(h)−L(h)∣>2ϵ]であるが、この確率をHoeffdingの不等式を用いて評価した。
- 前回の理想損失を0にできるh∗が存在していたときは、毎回のサンプリングでは高々(1−ϵ)の確率でしか正解できないということで上界を評価した。
- 今回は理想損失を0にできないし、h∗が理想損失をどれほどに抑えられるともわからない。
- ここをもうちょっと掘り下げてみる。
結局L(h∗)=0は何が重要だったか
L(h∗)=0ができる場合は、O(1/n)のオーダで収束するが、できない場合はO(1/n)のオーダで収束する。
L(h∗)=0⇒L^(h∗)=0になるので、経験損失が0になるものの中から、適格となるものを選べばよかった。これは結局、高々1−ϵの確率でしか正解できない+独立性があるということから、exp(−ϵn)で抑えられた。
だがこうとは限らないとき、その条件はないので、∣L(h)−L^(h∗)∣>ϵのような分布のすそについてHoeffdingの不等式で評価するしかない。その結果、必要データが増えてexp(−nϵ2)となってしまう。
仮説集合が有限ではないとき
前提条件として、Realizabilityの∃h∗,L(h∗)=0を外したが、今度はHが有限集合であるという仮説も外したい。
仮説集合が無限集合となるとき、Union Boundを使うことができなくなる。これの代わりに、McDiarmidの不等式やRademacher複雑度を使っていく。
モデルや仮説の仮定
非常に基礎的なモデルから解析していく。
- X⊂Rdが学習データ
- Y={+1,−1}がラベルである二値分類。
- 損失関数はすべて01損失。つまり、損失関数というのは条件を満たさない確率そのものである。
- 後程定義されるMcDirmidの不等式により、[0,1]でなくても、区間[a,b]でも問題はない。
追加の仮定は一切なし。
McDiarmid’s Inequality
関数fの引数が1つだけ違うものの値の変化の絶対値を抑えられる場合に成り立つ不等式。関数を「平均値を出力する関数」とみなせば、Hoeffdingの不等式そのものである。
ここで、関数fの取りうる値が[a,b]とすれば、∀i,ci=b−aであるといえる。この時、
exp(−∑i=1nci22ϵ2)=exp(−n(b−a)22ϵ2)=δ,ϵ=(b−a)2nlog(1/δ) なお、前と同様に両側で定義すると以下のようになる。
ここで、片側でもMcDiarmidの不等式は実用的である。なぜなら、f>E[f]+ϵの確率を評価できるから。
Rademacher複雑度による汎化誤差解析の流れ
n個の観測データに依存した確率変数G^n=suph∈HL(h)−L^n(h)を定義する。これは理想損失の最適解hを与えた時の損失と経験損失にhを与えた時の損失の差である。評価するのはこのG^n=suph∈HL(h)−L^n(h)であり、今まではLn,LでLについてのみ計算していた。
片側のMcDirmidの不等式でG^nを評価すると、以下のようになる。
G^n≤E[G^n]+(b−a)2nlog(1/δ) ここで、√の中のnが分母ではなく分子に来ているが、これはL自体の取る範囲が[a,b]であるので、McDiarmidの不等式として毎イテレーション評価するのは、平均をとるための係数1/nで割られたものであるということ。故に、毎イテレーションの間隔はb−aではなく、(b−a)/nである。
そして、E[G^n]を評価するのが、Rademacher複雑度である。
Rademacher複雑度は以下のように定義される。
Rademacher Complexity
ここで、σiは独立に生成した確率変数であるので、ランダムなノイズと言える。そんなノイズを正解ラベルとしてそこに適合させることは、モデルの表現力が十分に高ければ可能である。
これを踏まえて、ランダムなノイズに対して学習器がうまく適合させられるので、最悪の確率変数のセットを引いたときの、上式の下限は大きくなる。簡単に言うと表現力が高ければ完全にノイズですら学習でき、その結果Rademacher Complexityで大きな値を取る。
あらためてRademacher複雑度による解析
示したいものは、以下のものである。Rn(L)がRademacher Complexity。
少なくとも1−δ/2の確率で以下が成り立つ。
G^n=suph∈H{L^n(h)−L(h)}≤2Rn(L)+(b−a)2nlog2/δ これが成り立てば、L^n(h)−L(h)の評価は
r[L(h^)−L(h∗)≤ϵ]≥Pr[suph∈H∣L(h)−L^N(h)∣≤ϵ/2] という式で抑えることができることから、
少なくとも1−δの確率で以下の式が成り立つ。
L(h^)−L(h∗)≤4Rn(L)+(b−a)n2log2/δ 証明
まず、G^n=suph∈HL^n(h)−L(h)である。
そして、相補的なものとして、G^n−=suph∈HL(h)−L^n(h)を考える。
Pr[G^n>2ϵ]≤2δ,Pr[G^n−>2ϵ]≤2δ 以上の式が成り立つならば、以下のように合算できる。このように絶対値ついてるものは丁寧に符号を逆転させて外すとやりやすい。
Pr[suph∈H∣L(h)−L^(h)∣>2ϵ]=Pr[G^n>2ϵ]+Pr[G^n−>2ϵ]≤δ ということで、G^n,G^n−についてそれぞれ評価していきたい。
McDirmidの不等式を使いたい。G^n=suph∈HL^n(h)−L(h)について、データZ1,⋯,Znの関数として、1つだけZi→Zi′にしたとき、G^n′になったとする。
これの差の上界はL=1/n∑l(Zi,h)となるので、l(Zi,h)−l(Zi′,h)はたかだか[a,b]であることから、差の上界は(b−a)/nとなる。
これと、δ/2(2つを合わせるから導入した)というのを使ってMcDirmidの不等式を適用する。すると、1−δ/2以上の確率で、一番下の式が成り立つ。
Pr[G^n−E[G^n]>2ϵ]≤exp(−2(b−a)2nϵ2)G^n≤E[G^n]+(b−a)2nlog1/δ 次に、E[G^n]をRademacher複雑度で評価する。
すでにあるデータZ1,⋯,Znを使って、L^n(h)=1/n∑i=1nl(Zi,h)を定義した。
ここで別の独立なデータZ1′,⋯,Zn′を用いて、同様に計算したL^n′(h)も定義できる。
期待値自体は両方同じである。なので、G^nを展開した中身にZ→Z′にした。そして、赤い線の部分で平均した後でsup ≤ supしたものの平均が使われている。
そして、交換した中で、さらに展開してsuph∈Hn1∑i=1nl(Zi′,h)−l(Zi,h)を得る。期待値の計算に対称性があるので、符号はランダムに決まる→Rademacher変数を導入して書けるぞ!!!
E[suph∈Hn1∑i=1nl(Zi′,h)−l(Zi,h)]=E[Eσ[suph∈Hn1∑i=1nσi{l(Zi′,h)−l(Zi,h)}]] このようにRademacher変数を導入したので、次のように解析を進められる。
Rademacher変数の部分をそれぞれに分割すると、まったく同じ分布が2つ得られることから、最終的に足すことで上界として2Rn(L)が得られる。
よって、ここまでの議論をまとめると、
- 最適なL(h)=0となるhがなく
- 仮説空間Hが無限集合である
条件下でも、McDirmidの不等式でG^n=suph∈HL^n(h)−L(h)について評価し、Rademacher複雑度によるE[G^n]の評価で抑えるということができる。
確率1−δ以上の確率で、以下が成り立つ。
L(h^)−L(h∗)≤4Rn(L)+(b−a)n2log2/δ 今までとの違い
- 一番厳しかったのが、L(h)=0が存在し、仮説空間も有限集合である。この時は以下のようになり、一番厳しい評価である。
L(h^)−L(h∗)=L(h^)−0≤n1(log∣H∣+log(1/δ)) - 次は、L(h)=0が存在しないが、仮説空間が有限集合であるという前提条件。
L(h^)−L(h∗)≤n2(log∣H∣+log(2/δ)) L(h^)−L(h∗)≤4Rn(L)+(b−a)n2log2/δ どんどん上界としては緩くなっているのがlog で見て取れる。
(講義ノート)統計的機械学習第2回