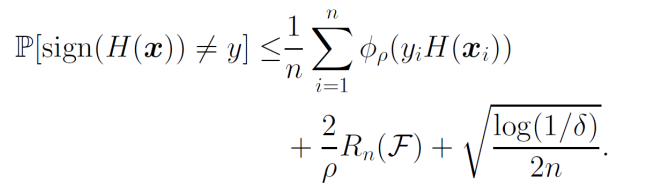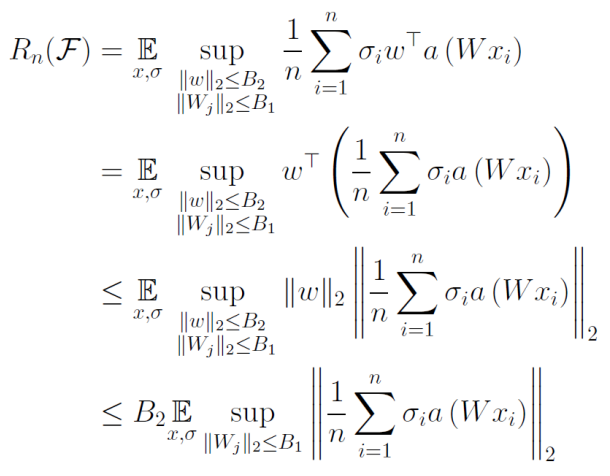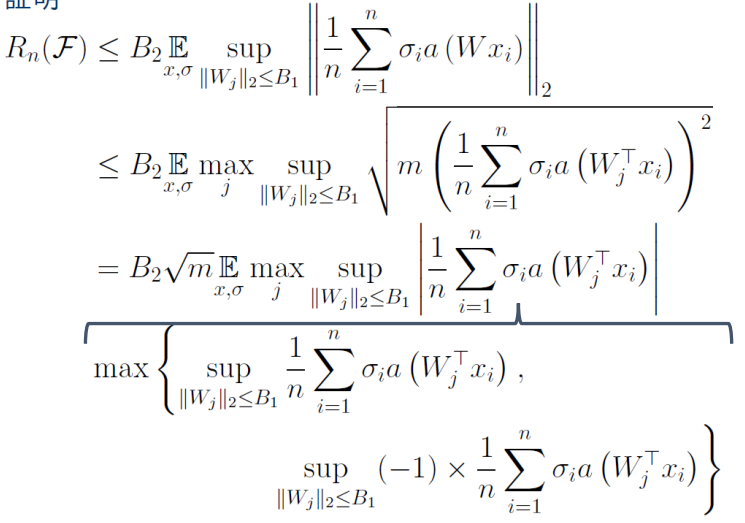前回はこちら。📄 (講義ノート)統計的機械学習第9回 。内容は以下の通り。
(講義ノート)統計的機械学習第9回 。内容は以下の通り。
Boostingの汎化誤差解析として、以下の式であった。
決定木の汎化誤差は以下のとおりである。
最後に、XGBoostの汎化誤差解析も行った。
Neural Network
NNの汎化誤差解析を考える。まずは簡単な3層のNNとする。
- 隠れ層はm層ある。
- 入力はx∈Rdであり、n個存在する。
- NNのパラメタは、3層なので2種類のみ存在し、第1層の重みはW∈Rd×mであり、2層目の重みはw∈Rmである。
- 活性化関数はa(x)=max(0,x)のReLUとする。
- これらを踏まえて全体のNNは以下のような関数と定義できる。
fθ:Rd→R,fθ(x)=wTa(Wx) 3層NNのRademacher複雑度
重みにはL2ノルムの上限がある。Wjは行ベクトルであり意味としては隠れ層の各ノードごとに重みをベクトルとして扱ったときにL2ノルムの上限がある。
∣∣w∣∣2≤B2,∣∣Wj∣∣2≤B2 そして、入力のL2ノルムの期待値の上界も考える。E[∣∣x∣∣2]=C
そして、以下のように3層NNのRademacher複雑度を抑えられる。
Rn(F)=Ex,σ[supfθ∈Fn1∑i=1nσifθ(xi)]≤2B1B2Cnm 証明
Holderの不等式で、wについてのノルムを外に出せる。次は、この行列の計算された2乗ノルムを計算したい。
ベクトルについてのL2ノルムの制約はあるが、行列についてはない。なので、どうにかして行列での評価をベクトルにしたい。
こういう時は、一番影響力がある一行(maxj)をとってきてそれをm倍するとすることで、上側から押さえられる。
そして、絶対値の外し方として、∣a∣=max(a,−a)として処理している。
重みを0にしたら項の値は0にすることができるんで、もし下手にマイナスに行くならば重みを0にすればいい。そして、max(a,b)≤a+bと抑えている。
こうすることによって、あとはReLUのリプシッツ定数が1なので普通にa()を外すことができ、結局この2つの項は同じ値をとるRademacher複雑度となり、したがって、以下のように評価できる。
Rn(F)≤B2m(2nB1C) 古典的にはこれのほうがいいが、最近はOverparameterizationのほうが望ましいということで、mも大きく理論的上界の意味があまりなくなる。
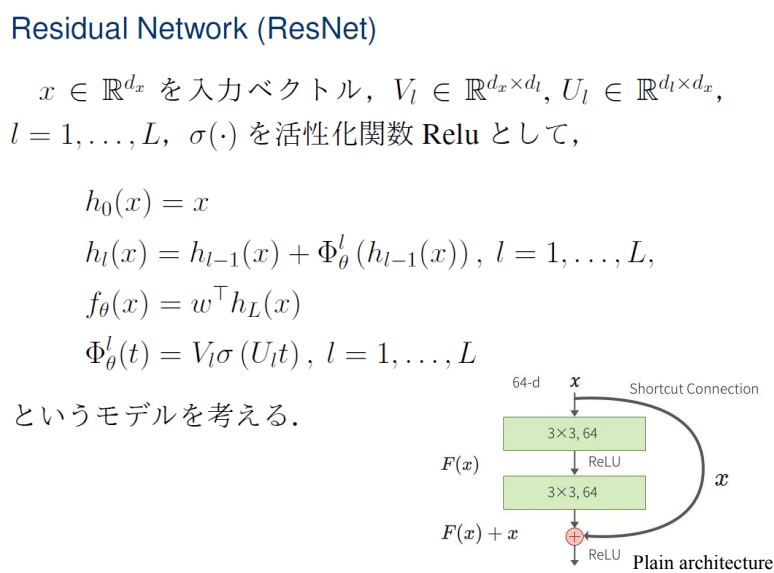
ResNetについての評価
ResNetのモデリング
上のhl(x)では、前のhl−1(x)と、その残差を足し合わせている。残差の計算はΦθlで計算できる。この残差の計算自体は、入力に線形変換+活性化関数+線形変換を施したものでVl,Ulが学習対象。
論文に従っての定義である。
(講義ノート)統計的機械学習第9回 。内容は以下の通り。