(講義ノート)統計的機械学習第13回

前回はこちら。📄(講義ノート)統計的機械学習第12回。内容は位相線形空間、コンパクト集合、ミンコフスキー和であった。

位相線形空間とは、関数ノルムというのを定義した関数でも線形代数っぽく扱えるようにしたもの。関数のノルムでよくあるのが、 $\sup|f(x)|=||f||$ であり、 $||f-g||= \sup| f-g |$

三角不等式、同次性/斉次性だけを満たす半ノルムというのも考えた。

||u+v|| \leq ||u|| + ||v|| \\ ||\alpha u|| =|a| ||u||

$u=0 \Leftrightarrow ||u||=0$ については成り立たず、 $\Rightarrow$ は成り立つが逆は成り立たない。

距離空間においてのコンパクト性も考えた。

$K \subseteq X$ が点列コンパクトであるとは、 $K$ が位相(開集合の集合族)であるが、に含まれる任意の点列 $(x_n)_{n \in \mathbb{N}}$ に対して、 $K$ の中の点に収束する部分列が存在することである。

位相空間論においての、一般的なコンパクト性とは「有限の大きさを持つ」という意味でしかない。位相空間 $(X,A)$ がコンパクトであるとは、 $\bigcup_{i=1}^m U_i \supseteq X$ となるような被覆 $U$ があるということ( $X$ に含まれていないような元を含む集合もあり得る)。そのうえで、どんな $\{ U_i \}_{i=1}^m$ でもその中にある有限個の要素からなる集合 $\bigcup_{j} U_j \supseteq X$ になれるということ。

線形汎関数と劣線形性も考えた。半ノルムのように汎関数 $l: X \to \mathbb{R}$ に関して、三角不等式と斉次性は満たすのならば劣線形汎関数である(半ノルムみたいだよね)

l(x+y) \leq l(x) + l(y) \\ l(\lambda x) = \lambda l(x)

有名なものとしてゲージ汎関数がある。

$\mathbb{R}$ 体上のノルム線形空間 $X$ の部分空間 $K$ が凸集合であるとする。0を内点として含むとする。

ゲージ汎関数は以下のもの。 $x$ に $1/a$ をしても $K$ に含まれるとき、そうなる一番小さい $a$ ということ。

つまり、許される区間 $K$ に与えられた値を押し込むのに、一番最低限で割るいくつが必要か？ってこと。

p_K : X \to \mathbb{R}_{\geq 0} \\ p_K(x) = \inf \{ a \in \mathbb{R}_{\geq 0} | \frac{1}{a} x \in K\}

A \pm B = \{ a \pm b | a \in A, b \in B \}

ミンコフスキー和/差がある。2つの集合 $A,B$ の各元についてそれぞれの和/差を $|A| \times |B|$ 通りエミュレートしたい。

凸集合 $A,B$ のミンコフスキー和/差は同じく凸集合になる。

ハーン・バナッハの拡張定理

部分空間 $Y \subseteq X$ 上で $g$ よりも $p$ が常に上に来るなら、 $X$ 上でも $g$ を拡張することができるし、同様に $p$ よりも常に下に来る。

つまり、部分空間で線形汎関数 $g$ を見つけられたら、それは全体の空間でも成り立つということ！

$p$ は劣線形汎関数であるが、凸関数もそれの一種類である。なので、ある区間だけで凸関数より下なら、すべての区間でもそりゃ凸関数の下だからだよね。

これはあくまで存在を保証しているが、具体的にどう構築するのかはわからない。

ノルム線形空間での分離超平面定理

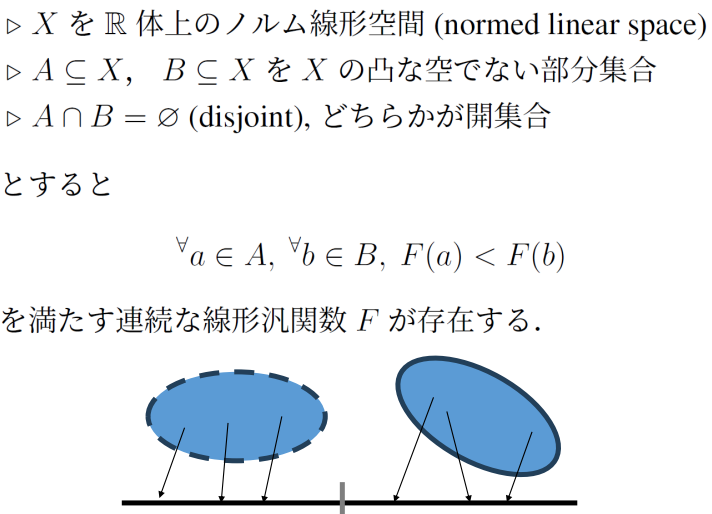
2つの集合 $A,B$ がかぶっておらず、どちらかが開集合であるとする。

この時、何かしらの超平面が存在し、 $A,B$ の元をそれぞれきれいに分けることができるという意味。

証明

ミンコフスキー差を考える。いずれか一方が開集合なので、 $K$ も空ではない開凸集合である。

次に、 $x_0 \notin K$ となるようなものを選ぶ。 $y_0 \in K$ だとして、 $x_0$ と $y_0$ 差 $x_0^-$ を考えられる。

また、差の $K^- = K - \{ y_0 \}$ で再びミンコフスキー差を考えられる。(自分自身の元の1つと全部ミンコフスキー差を計算する感じ) $K^-$ 自体も空ではない開凸集合。

$0=y_0 - y_0 \in K^-$ は成り立つが、 $K^-$ はゲージ汎関数である。なぜなら、 $K^-$ は凸集合で0を含むので、必ずゲージ汎関数 $p_K^-$ を作ることができる。

$x_0$ は0でもなく、 $K^-$ にも含まれていない。そして、 $X_0^-$ を1点 $x_0^-$ だけで構築される区間(span演算)を作っている。1点しかないので、一次元線形空間である。 $x_0^- \in X$ である以上、それをもとに拡張した一次の線形線形空間も $X$ の部分空間である。そして当然だが $\lambda=0$ とすれば $0$ も入っているとわかる。

$X_0^-$ 上の汎関数 $f$ を $f(\lambda x_o^-) := \lambda$ と定義すると、 $f$ は線形汎関数(線形空間から実数へ写像する関数)。 $X_0^-$ 自体は1点だけで構築された一次元線形空間なので、 $X_0^-$ 上とは $\lambda x_0^-$ と書いていい。