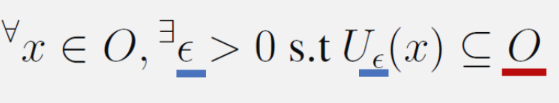Sen(Qian)’s Memo

前回はこちら。📄(講義ノート)統計的機械学習第10回 。内容は以下の通り。

3層のDNN(隠れ層が1)のもののRademacher複雑度の抑え方は以下の通り。$B_1, B_2$は係数の上界であり、$m$は隠れ層のノード数。

ResNetについては、📄2019-NIPS-Are deep ResNets provably better than linear predictors? がありそれについて、以下のようにResNetのRademacher複雑度を抑えらえれるとわかった。

通常の全結合ネットワークとは分子から$\sqrt{m}$が消えていることが違いであり、これは隠れ層のノード数がいくら増えたとしても、Rademacher複雑度に影響しないという評価である。影響するのは、各パラメタの上界だけ。

Neural Networkは十分なパラメタと適切な活性化関数を設定すれば、1層の隠れ層だけを持つNNとして、任意の連続な関数に好きな精度で近似できる=稠密(ちゅうみつ)である。

なお、稠密であることと完備性があるというのは同じではない。有理数は実数に対して稠密であるが、無理数がないので穴だらけですよね。

つまり微分できる関数ならテイラー展開、マクローリン展開に従って多項式で近似できる！というようなことを言っている。

厳密に定義するなら以下のように定義されている。

無限次元のベクトル=関数による空間=関数空間、考えられるといろいろ便利ですよね？

基底について、部分集合$B \subset V$が基底というのは、$B$が有限集合である必要はなく、$B$自身の有限部分集合で、もともとの$V$に含まれる任意の元を構築できるベクトル集合を持てるなら$B$は基底。

ただこれだと、$\forall x \in V$は有限個のベクトルで表現する必要があるが、$x = \sum_{i=1}^\infty a_i v_i$というような無限次元の表現が出てきてしまう。例えばフーリエ変換とか、カーネル法による

この無限級数の表現が収束するかのような議論が必要になり、そのために位相が求められる。

なので、有限個の基底という概念からさらに進化させて、無限個を許容しそれの収束性なども証明し、それが「位相」となる。

一部だけかいつまんで。

ある集合に、「位相」を定義したものが位相空間。位相を定義するのに以下のものが必要。

1. 点の近傍
2. 開集合
3. 閉集合
4. 閉包

これら4つはそれぞれ相互に定義可能であり、1つ定義できればその他はそれを使い同様に表せる。

部分集合系$O$について、以下の3点が成り立てば$O$は$X$の位相であり、$(X,O)$は位相空間とい。

例)$X$が実数なら、$O$は実数区間を元とする集合みたいな。

1. $\phi, X \in O$　空集合と$X$自身は含む。$a$に対して$[a,a]$みたいな感覚。
2. $\forall U_1, U_2, U_1 \cap U_2 \in O$　位相に含まれる元の積集合も必ず位相に属する。
3. 任意の添え字集合$\Lambda$について、$\bigcup _{\lambda \in \Lambda} U_{\lambda} \in O$が成り立つ。　任意の添え字で$O$に含まれる元$U_\lambda$の和集合をとっても絶対に入っている。

また、言い方として、$O$自身を「開集合」と定義しちゃってて、$X$自体を位相空間と言ったりする。

もう1つの例は有限集合$S=\{a,b,c \}$について、$O=\{ \{a\}, \{a,b\}, \{a,c\}, S \}$だというもの。これも確かに位相空間$(S,O)$である。

なので、開区間はもう定義できた。

なお、集合の集合を集合族、集合系と言ったりする。族はその集合の集合に何かしらの操作をすることを前提にしているが、系の場合は集合の集合自体に興味があり操作なくていいもの。

開集合が定義されたとき、開集合の補集合が閉集合である。

定義は開集合と似ているがひっくり返したもの。$\mathcal{F}$だとする。

1. $\phi, X \in O$　空集合と$X$自身は含む。
2. $\forall U_1, U_2, U_1 \cup U_2 \in O$　位相に含まれる元の和集合も必ず位相に属する。
3. 任意の添え字集合$\Lambda$について、$\bigcap _{\lambda \in \Lambda} U_{\lambda} \in O$が成り立つ。　任意の添え字で$O$に含まれる元$U_\lambda$の積集合をとっても絶対に入っている。

連続ならば、行った先の位相空間から元々の位相空間への逆像があるということ。

開集合から写像した先から逆像で戻したらちゃんと開集合になるということ。

ここで、逆像と逆写像とは違う。写像の定義として全単射があるがそれを満たさなくてもいいということ。

連続というのは、$\forall \epsilon >0, \exist \delta > 0$で、$|x -x_0| < \delta \Rightarrow |f(x) - f(x_0)| \leq \epsilon$である。これを先ほどの集合に転用させると、以下のようになる。

つまり、写像した先の変動が微小というのを、$U_*$というもので表現した(例でいうと開区間がそれにあたる)

$O$が開集合ならば、以下のが成り立つ。

$X$を集合とする。に変数関数$d : X \times X \to \mathbb{R}$が、任意の$a,b,c \in X$に対して、以下が成り立つなら、$(X,d)$は距離空間という。

1. 正定値性　$d(a,b) \geq 0$であり、$a=b \Leftrightarrow d(a,b)=0$でもある。
2. 対称性　$d(a,b)=d(b,a)$
3. 三角不等式　$d(a,b) \leq d(a,c) + d(c,b)$

この距離空間について、$U_\epsilon (a) = \{ x \in X | d(x,a) < \epsilon \}$を、中心$a \in X$、半径$\epsilon$の開球という。

不等号は等号を含まない！開球なのに含まない！理由はちゃんとある！

そしてこの開球を用いて、開集合、閉集合を定義することもできる。

1. $A$が開集合とは、以下のようなことである。つまり、開集合のどんな元を選んでも、それを中心とした何かしらの半径の開球は、開集合$A$自身の中に含まれている。
   1. 実際どんな開集合$[a,b]$を選んでも、なんでもいいので距離の尺度$d$(ユークリッドと考えてもいい)があるとして、ある$\epsilon$があって、$d([a,b], [c, d]) > \epsilon$となるすべての$[c,d]$は開集合なので、確かになりたつみたい。
   2. つまり、元(開区間)の近傍の性質によって元(開区間)全体から成る本体の集合(開集合)の性質が定義される。

1. $B$が閉集合とは、以下のようなことである。

逆像は等号成立が非常に多いので、使いやすく、連続の定義はよって逆像で定義している。

位相空間$(X,O), (X^\prime, O^\prime)$の間の写像$f : X \to X^\prime$が連続であるということは、

が成り立つということ。任意の$X^\prime$の開集合の逆像が$X$の開集合であれば、$f$が連続であるという。

移した前での近傍のものは、移した先でも近傍であってほしい。

$x \in X$の$X$における近傍$V(x) \subseteq X$とは、ある開集合$U \subseteq V(x)$が存在し、$x \in U \subseteq V(x)$、

$x$の近傍とは、$V(x)$という集合族の元の集合がすべて$x$を含むものである、というもの。$1$を相手と考えるなら、$\{ \{1\}, \{1, 2\}, \{1, 3\}, \{1, 3, 4\} \}$みたいな。開区間も集合であるので、$\mathbb{R}$という大きな集合に、開区間が集合として包含されるということ。

さらに、$V(x)$が開集合ならば、開近傍である。

位相空間$(X,O)$を考える。$A \subset X$だとする。

• $x$が$A$の内点であるとは、$\exist U \in O, x \in U \subseteq A$である。
  • ある開集合$U$があり、それは$x$を元として含み、部分集合$A$も$U$を含むというもの。
  • 近傍の定義そのままで、$x$の近傍$V(x)$の内点が$x$である。
• 位相空間のみならず、距離まで完備である距離空間の場合、内点であるというのは、以下の数式である。
  • $U$が開球の$U_\epsilon$である。

• さらに言えば、$X$が実数体$\mathbb{R}$上のノルム線形空間の場合、以下である。
  • どんな向きのベクトル$y$であっても、ある$\epsilon$だけ足したら$A$に入ってるなら内点。
  • $U_\epsilon$がさらに具体的になった。

すべての内点の集合が内部。

内点についてはさらに、$X$が実数体$\mathbb{R}$上のノルム線形空間の場合を考える。上で解説した通り、線形空間に含まれるどの向きのベクトルでも少し動いてもちゃんと収まるということ。

この時、$0 \leq t < \epsilon$と0も許容する=ギリギリ境界上でもOKならば、それはコアである。

ことばの定義みたいなもの。

• コア＝内部＋境界
• 全部＝コア＋外部

内部は$A^\circ$であり、外部は$A^c$と書く。境界は$\partial A$と書く。

$A$を位相空間$X$の部分集合とする。$A=A^\circ$(自分の内部は自分と同じ これから示すように開集合ならば必ず成り立つものである)であるとする。

$x \in A^\circ$の$A^\circ$における開近傍を$V(x) \in A^\circ$とすると、以下を満たす開近傍$V$が存在する。

$A^\circ$、つまり内部に含まれるすべての内点の開近傍について、それの和集合は$A^\circ$つまり内部と同じである。

内点の定義により、$\forall x \in A^\circ$について、$x \in U(x) \subseteq A$となる開近傍$U$が存在する。なので、先ほどの定義から、すべての$x$について考えれば$A^\circ \subseteq \bigcup_{x \in A^\circ} U(x)$となる。

$A=A^\circ$という仮定がないのでちょっとむずかしい証明になる。

$U$を$A$に含まれる任意の開集合とする。この時、$x \in U \subseteq A$により、$x$はAの内点。任意の開集合について、$U \subseteq A^\circ$(内点なので内部の中であるよね？)が常に成り立つので、$\bigcup _{x \in A^\circ} U(x) \subseteq A^\circ$も成り立つ。

なので、$A^\circ$、Aの内部は開集合。

$A$は位相空間$X$の部分集合である。この時、$A$が$X$の開集合$\Leftrightarrow$$A^\circ = A$である。

今までの流れを踏まえてこれを考えたらこのようになった。

$A$を位相空間$X$の部分集合である。$A^\circ$は$A$に含まれる最大の開集合である。

微分は定義するとき以下の時のようになる。これは右極限、左極限が必要であるが、実は$a$の周り$(a - \epsilon, a + \epsilon)$で$f$が定義されている必要がある。つまり、$a$が$f$の定義域の内点である。

$x \in X$が$A$の触点であるというのは、$x$の任意の開近傍$U(x)$が$A$と交わることである。

なので、触点は$A$の内部か、境界上にある。(内部がすべて触点というわけではない)

$A$の触点の集合を$A$の閉包という。閉包は$\bar{A}$とあらわす。

内部か境界上にあるので、$\bar{A} = A^\circ \cup \partial A$である。

そしてさらに自明にではあるが、$A \subseteq \bar{A}$である。

$x \in X$が$A$の集積点であるということは、$x$の任意の開近傍$U(x)$が$x$をのぞいて$A$と交わること。

ここで重要なこととして、集積点自身が$A$に含まれなくてもよい。あくまで任意の開近傍が$A$と交わればよい。

ドーナツみたいな感じ。触点から自分自身が含まれるを除いた。

定義からして、$A$の集積点は閉包に含まれている。集積点のすべての開近傍は$A$と交わるから。

集積点ではどんな小さい開近傍であっても$A$と交わるので、本当に$A$とスレスレか$A$の中にいるとわかる。周りのどの点でも$A$である。

すべての触点の集合が閉包であるがそれが閉集合だと示す。

閉包の補集合が開集合であることを示せばいい。開集合の定義が明確である以上こちらで証明するというテク。

補集合に含まれる元は$A$と交わらず、閉包の定義からして当然のように$\bar{A}$とも交わらない。よって、補集合に含まれる点の任意の近傍も補集合に含まれる。これって内点そのものであるので、内点の集合=内部=開集合である。

これは逆も成り立つ。

$A$を位相空間$X$の部分集合だとする。稠密(ちゅうみつ, dense)であるとは、閉包$\bar{A}$について、$\bar{A}=X$である。

• $A$の閉包=触点(すべての近傍が$A$に含まれるような点)をすべて集めた集合ではあるが、これが位相空間$X$全体を覆っているという状況。
• $x\in X$の近傍には$a \in A$がいる。これは極限や近似として使える。
• 例えば実数に対しては有理数$\mathbb{Q \subset R}$は稠密。有理数自身は少しでも動けば=任意の近傍、実数になる。なので、有理数の閉包は実数。