強化学習第2回講義

前回はこれ。

状態 $s$ からポリシー $\pi$ に沿って得られる利得の条件付期待値を以下のように定義する。これはState-Value Function。これで、状態 $s$ にいるときの価値というのを定義できる。価値は未来永劫にわたって得られる利益の和(さすがに発散するので $\gamma < 1$ の係数を毎回かける)

V^{\pi}(s) = \mathbb{E}[R_t | S_t = s]

似たように、状態のみならず、行動までわかっているときの期待値はAction-Value Functionという。

Q^\pi (s,a) = \mathbb{E}[R_t | S_t = s, A_t = a]

もし、 $Q^\pi (s,a)$ がわかっているなら、最適なポリシーは毎回 $a = \argmax _a Q^{\pi^*} (s,a)$ を選ぶこと。これは常に決定的である。

そして、2つの式の間では以下の関係が成り立つ。すべて合算する感じなのでそれはそう。

V^\pi(s) = \sum _{a \in A} \pi(a | s) Q^{\pi}(s, a)

Bellman Equationを導入する

以下のような式変形で、

状態 $s$ からのポリシーに従って得られるActionの $a$ の期待値 $a \sim \pi$
今の状態 $s$ と取るActionからの次の状態の期待値 $s^\prime$ 。 $s^\prime \sim p(s ^ \prime | s, a)$

についての期待値として、記述することができる。

真ん中の説明 $s \to s^\prime$ へ遷移したときの得られる利得。
右は $\gamma V^{\pi}(s^\prime)$ であり、次のState Valueである。

毎回の利得は $R_t = r_t + \gamma R_{t+1}$ が条件付きで成り立つ。これをもとに、ポリシー $\pi$ を期待値に分解すると、上に述べた2つの総和となり、加算される。そして期待値の中は漸化式で再帰的に同じものが現れる。

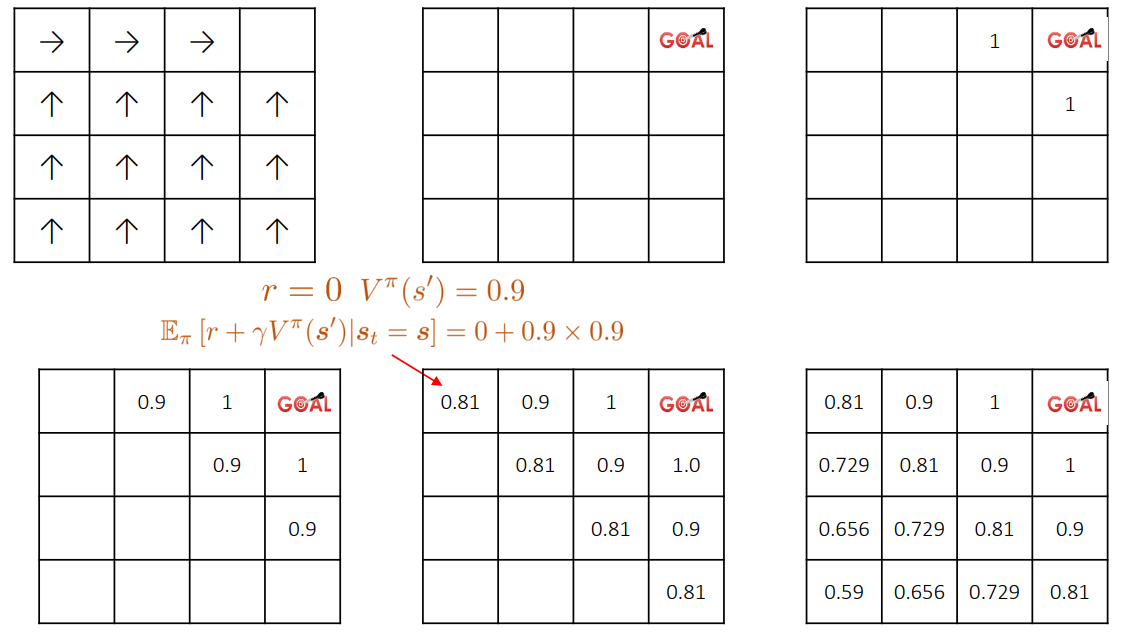
上があるポリシーに従った各状態=地点における価値 $V^\pi(s)$ である。

SARSA

Bellman Equationを利用したOn-policy(=今集めているデータからわかる状況で、次のアクションを決定する。→決めたアクションをもとに、データを収集する)推測である。

次の目的関数を最小化したい。

L(w) = \mathbb{E} _{s \sim d^\pi, a \sim \pi} [(r + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t, a_t)) ^ 2]

つまり、今いる時点での価値 $Q(s_t, a_t)$ と、動いた後に得られる価値と将来の価値に減衰率を乗じたものと一致させたいように学習する。

なお、Gradientは以下のようになる。

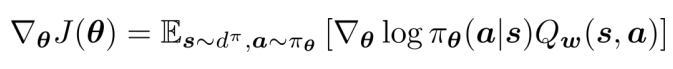
Bellman Operator

Bellman Operatorとは、Action Value Functionについての将来を漸化式のように予測したものである。

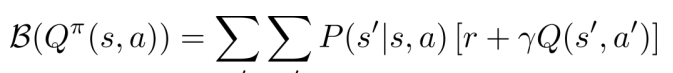
Bellman Operatorによって最適なポリシーに収束するらしい。

Optimal Value Function

さっきのValue Functionに対して、最適なポリシー $\pi^*$ を与えたときの関数。 $V^*(s), Q^*(s,a)$ である。

そしてそれは1つだけActionを選ぶので、通常の $Q^{\pi^*}(s,a)$ を代入して展開するのと同じように、 $V^{\pi^*}(s)$ による漸化式になる。

Q ^{\pi^*} (s,a) = \sum_{s ^ \prime} p(s ^ \prime | s, a) [r + \gamma V ^ {\pi ^ *} (s ^ \prime)]\\ V^{\pi^*}(s) = \max _{a \in A} Q ^ {\pi ^ *}(s, a) = \max _a \mathbb{E}[r + \gamma V^{\pi^*}(s ^ \prime) | S_t = s, A_t = a]

Q-learning

最適なaction-value functionの $Q^{\pi^*}(s, a)$ を見つけたい。そのために、以下の式で学習をする。

Q(s, a) \leftarrow Q(s, a) + \alpha[r + \gamma \max _a Q(s ^ \prime. a) - Q(s, a)]

Bellman Equationで得られた今後のOptimalなPolicyをとった時の予測と、実際にActionの $a$ で得られた報酬の差を、一定の学習率で更新させていく。

Replay Buffer

強化学習で遷移情報を集めるときに、そのまま使うと自己相関があまりにも強すぎるので(前後するフレームなので)、それを使わずにまずはReplay Bufferにためておく。そして、学習時はReplay Bufferから溜まっているサンプルをランダムに選択して、ミニバッチを作成する。これは以下のDQNの性能に大きく貢献している部分でもある。