Sen(Qian)’s Memo

非常に基礎的なモデルから解析していく。

• $\mathcal{X} \subset \mathbb{R}^d$が学習データ
• $\mathcal{Y} = \{+1, -1\}$がラベルである二値分類。
• 損失関数はすべて01損失。つまり、損失関数というのは条件を満たさない確率そのものである。

仮説は2つの仮定の下で行う。

• 仮説空間$\mathcal{H}$は有限である。
• 期待損失$\exist h^* \in \mathcal{H}, L(h^*) = 0$

複数の最小化させる$h$は存在するので、一応集合ではある。だが、1つだけだと扱ってもまあよく見える。

前述の仮定の下(特に仮説空間が有限)で、$\hat{h} \in \argmin _{h \in \mathcal{H}} \hat{L}_n (h)$つまり経験損失を最小化させるものを$\hat{h}$だとすると、少なくとも$1 - \delta$以上の確率で

仮説空間が複雑になればなるほど、確率が小さければなるほど上限が大きくなる。

$L(h^*)=0 \Rightarrow \hat{L}_n (h^*) = 0$。真の損失関数を0にするものが存在すれば、それは何個のサンプルについてであろうとも、経験損失は当然0にできる。なので、$h^* \subseteq \hat{h}$であるといえる。なので、$h^*$よりも広い集合$\hat{h}$について、すべて$\epsilon$に収まるのは最低でも$1 - \delta$以上の確率であると示すという感じ。

まず、$L(h) > \epsilon$となるような仮説空間$\mathcal{H}_{> \epsilon} \subseteq \mathcal{H}$を考えることで、以下のように求めたい確率を同値変換できる。これで集合についての議論となった。

下から2つ目の式は、$\hat{h}$に限定しないような$h$ならばよいということで、右辺は左辺以上である。左辺の直接計算は難しいので、右辺で抑える。

そして、$\exist h, L(h) > \epsilon$について、以下が成り立つ。間違える率が$\epsilon$以上ということ。

すべて独立同分布からとっているので累乗にすることができ、毎回最高でも正解する確率は$1 - \epsilon$である。そこから、$1-x \leq \exp(-x)$を使った。

そのうえ、Union Bound(集合の元についての討論なら、集合全体について合算して上限とする)を使える。

ここでは、集合の元すべてで抑えている。

したがって、ここまでの議論をまとめると以下のようになる。

最後に$\delta$を定義してあれば、証明したいものが得られる。

Q.E.D.

これは一様収束。まず$N_0$を定めて、そこからすべての$\mathcal{X}$の元が$N_0$基準とした収束速度だと保証する。$N_0$は$\epsilon$にのみ依存する。

下は各点収束。$N_0$は$\epsilon, \mathbf{x}$に依存する。

すべての元がそれぞれ収束するとしても、同じ基準$N_0$で収束しないといけないルールはない。

• 一様収束する→各点収束する
• 一様収束する$\Leftrightarrow \lim_{n \to \infty} \sup_{x \in \mathcal{X}} |f_n(x) - f(x)| \to 0$
• 連続関数の一様収束極限も連続関数。
• $f_n$が$f$に一様収束するときに限り、微分積分と和を交換できる=項別微積分ができる

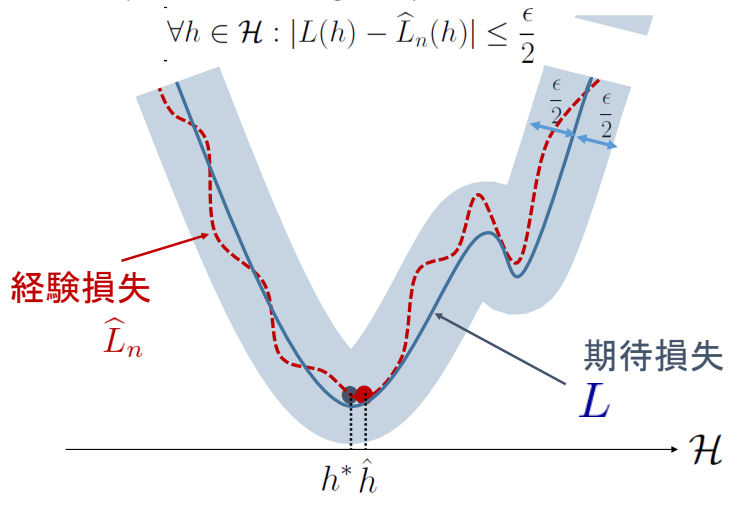
定義からして、一様収束するなら絶対に同じ収束速度で、どの仮説であっても$\epsilon / 2$に収まるということ。

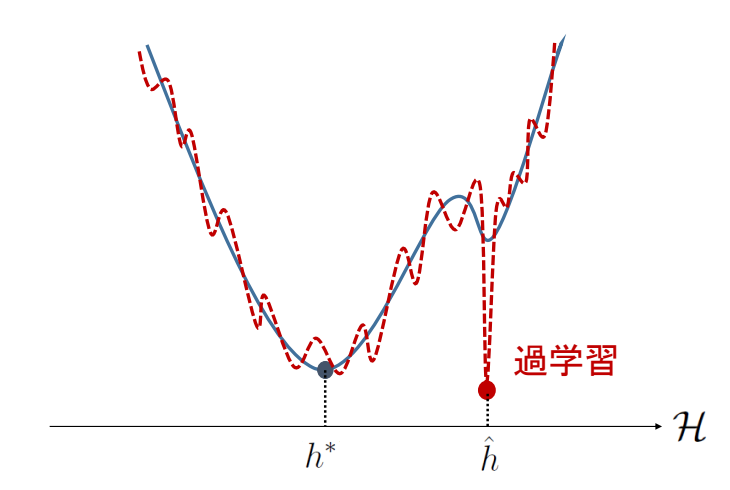
このように、サンプルから得られた経験損失で過学習は起きることがあるが望ましくない。各点収束では、過学習の点の収束速度が他と違うということになる。だから一様収束で議論するべきである。

具体的に式で定義すると、以下のようになる。

左辺には$h^*$があるが右辺にはない。$\forall h \in \mathcal{H}$の中で一番広がる部分がどこか？で言い換えられる。→$h^*$が具体的になんであるのかを見なくていい！また、$\hat{h}$が損失関数$L_n$によって決定されている関係上、$L_n$は独立な変数として扱えないのも面倒だが、右辺ではその問題を無視できる。

では、これが正しいのを証明する。

$\sup_{h \in \mathcal{H}}|L(h) - \hat{L}_n(h)| \leq \epsilon / 2$が成り立つならば、

• $L(\hat{h}) - \hat{L}_n (\hat{h})$は$h \in \mathcal{H}$なので、$L(\hat{h}) - \hat{L}_n (\hat{h}) \leq \epsilon / 2$が成り立つ。
• $\hat{L}_n(h^*) - L(h^*) \leq \epsilon / 2$も同様に得られる。

よって、以下のようになる。与えられた条件は理想損失と経験損失の差を限定させているが、何とか理想損失だけで差を出したい。ここでは、

• $L$から経験損失の$\hat{L}_n$2つ作り出す。この2つは、既存の$L$とCouplingして、条件を使えるようにする。
• 作り出した部分$\hat{L}_n(h^*) - \hat{L}_n(\hat{h}) \geq 0$は正であるという性質が好都合。不等式の符号がそろう。

よって、確率の中で改めて考えると、

このように計算ができる。Q.E.D.

結局、一定の範囲内に抑えられるというのがやりやすいので変換してやっているだけ。