Sen(Qian)’s Memo

前回はこれ。

📄強化学習第2回講義

• State-Value Function　今の状態から将来的に遷移した時の利得の和の期待値(減衰率$\gamma$)

• Action-Value Function　今の状態からアクション$a$を取ったときの利得の和の期待値(減衰率$\gamma$)

Q-learningとは、うまく$Q(s,a)$を予測するのが目標。以下のように、Bellman optimality equationを用いて毎イテレーション更新していく。

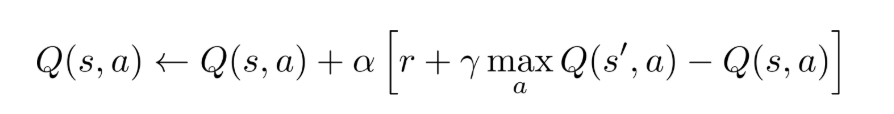
大量のデータセットとして、$\{ (s_i, a_i, s ^ \prime _i, r_i) \}_{i=1} ^ N$があるとする。それぞれ、(今の状態, 取るアクション, 遷移した先の状態, アクションによる利得)である。

参考: https://horomary.hatenablog.com/entry/2021/02/06/013412

DQNでは、表現力豊かなDNNを用いて、$Q(s, a)$を予測する。具体的には、以下のように二乗誤差を最小化するように動くらしい。

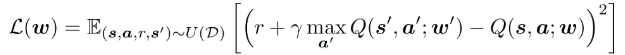
しかし、Q-learningの上の式では、将来の報酬を$\max$で決定しているが、エージェントが偶然高い値をとる(最初の収束してないときなどで)と、次のループ以降のQ値を高く予測してしまうといバイアスが働くということ。

これに対処するために、Double-Q-learningという手法がある。以下の通りにやる。

1. $Q_A, Q_B$という2つのQ値推測関数と、始まり
2. 次のループを繰り返す。
   1. $Q_A, Q_B$両方の判断に従って、とるアクション$a$、遷移した状態の$s^\prime$を得る。
   2. $A, B$１のどちらかをこのループで更新するかをランダムに決める。
   3. 選ばれたほうを$Q^+$とする。選ばれなかったほうを$Q^-$とする。
      • 遷移した状態から、取る最適な行動による利得の最大化をする。これは今のポリシーに基づく$V(s^\prime)$であるともいえる。
      $a ^ * = \argmax _a Q^+(s ^ \prime, a)$
      • これを使って更新していく。未来の最適にあたる$Q(s^\prime, a)$は、選ばれなかった方のQ値推測関数で計算する。
      $Q^+(s,a) \leftarrow Q^+(s,a) + \alpha(s, a)(r + \gamma Q^-(s ^ \prime, a ^ *) - Q^+(s, a))$
   4. 最後に$s \leftarrow s ^ \prime$にする。

これによって、Co-Trainingのような冗長性を持たせることができ、1回まずい更新したとしても、相方の除去能力によってある程度助かる。

参考資料: https://qiita.com/sugulu_Ogawa_ISID/items/6c4d34446d4878cde61a

Duel Deep Q-learningという手法もある。予測するとき、普通にQを予測するのではなく、

• $s$にのみ依存する$V^\pi(s)$
• アクションと状態両方に依存する$A^\pi(s,a)$

に分けて、それを足し合わせて予測するというものである。これはQを状態$s$だけで決まる部分$V(s)$と、行動次第で決まる部分$A(s, a)$に分解して、それを加算する。

しかし、足すだけだと、$Q$にはならないので、以下のようにActionの平均を差し引くことで、実質的に$V(s)$のぶんをけしている。

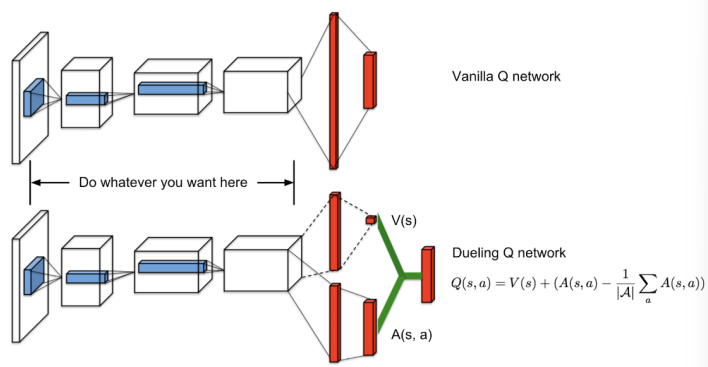
こうすることで学習がさらに早くなり、収束しやすくなる。

参考: https://qiita.com/fujitagodai4/items/62100d63b43cd518c127

マルコフ過程の学習をしたいので、1つ前の状態や行動からのみ、次の状態が決まるというもの。しかし、時系列順に画像を入力させると、複数前のものからの予測などになって、覚えてほしくないものも覚えてしまう。

Replay Bufferという手法をここで導入する。サンプリングされたデータをためて、そこから決まったルールで選択するというもの。

誤差が大きいほど、重要度が高く選ばれやすい=学習に取り込まれやすい

既存のQ-learningのDNNの全結合層$\mathbf{y} = W \mathbf{x} + \mathbf{b}$を以下のものに切り替える。

$W, \mathbf{b}$を置き換えた感じ。期待値から推論ごとに$\boldsymbol{\epsilon}$というNoiseを加える。この条件下で学習することで、より過学習しない？

参考: https://qiita.com/keisuke-nakata/items/2767c287e4ee7a71716c

強化学習において、今までは収益の期待値である$V, Q$を学習で求めていたが、期待値ではなく分布が重要である、というもの。

Wasserstein距離というものを考える。これは最適輸送に基づいた、分布の間の距離であり、距離の公理を満たす。具体的には2つ分布の間の最適輸送による最小のコスト(の$1/p$乗。これはあらかじめ人が$p$の値を決める)

Bellman Operatorを以下のような分布の形にする。報酬Rのランダム性、遷移のランダム性が本来のBellman Operatorと違うところ。

ちなみに、不動点をただ1つもつ縮小写像である。

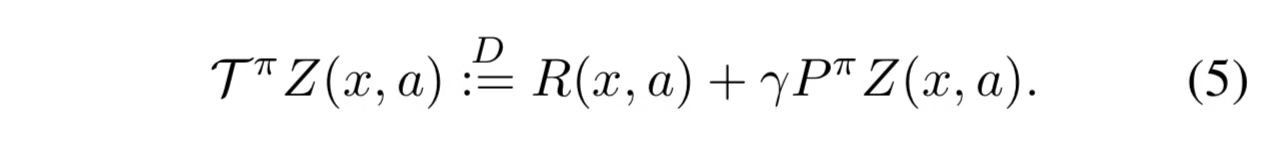
上の部分は2つの分布の距離を比べている？割引率を掛けて分布を縮めてから、報酬$R$を足して平行移動する。最後に$\Phi$で横幅を戻した分布を、比べたいものとの距離を比べている感じ？

いろいろよくわからない。