ここで第1回と書いてあるけど第1回はガイダンスだからこれ授業では第2回だ。
強化学習のためのMLの基礎
わかってるものはさすがに飛ばす。
Maximum Entropy Principle
条件が与えられ、それ以外のものがわからないときに分布を仮定するなら、エントロピーが最大のものを仮定しなければならない。
つまり、一様分布とできるだけ距離が近い=KLダイバージェンスが近いものを選ばないといけない。
なお、KLダイバージェンスは交換則が成り立たない。成り立つJSダイバージェンスなどがある。だが、とにかく計算がしやすいのがいいところ。
例えば、ボルツマン分布のかたちをしている、期待値が○○であるとわかっているならば、以下の条件でラグランジュの未定乗数法で計算できる。
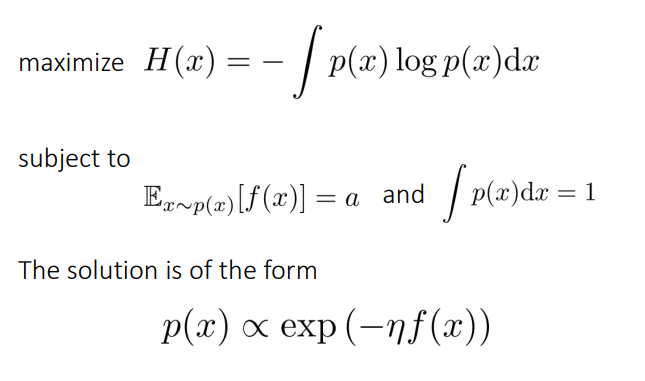
Bandit Problemとベイズ最適化
強化学習の流れ
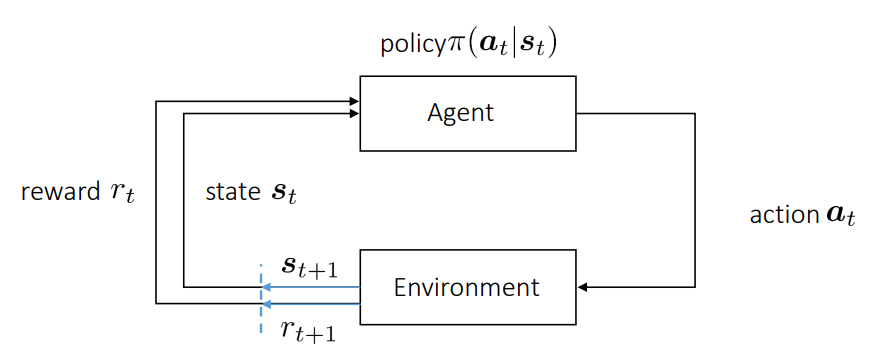
状態で、行動を取る事で、次の状態を得る。この1つ前のものだけを依存するのはマルコフ過程という。強化学習の目的は、以下のように直近の利得を重視しつつ=移動指数平均を最大化したい。直近の利得としているのは、で実現させている。昔の利得を減衰させている。
これの決定する順序は以下のように、で、「環境→行動→利得」となる。
K-armed Bandit Problem
K台のスロットがあって、それぞれガウス分布に従った違うかもしれない中央値の利得を出す。どのようにして利得を最大化させる?
Action Value
Action Valueは、指定のActionを取ったときの利得という条件付期待値である。
これを推定するので一番簡単なのは以下のようにベイズ推定をすること。

分子は時刻での行動による利得の総和。分母は時刻で試した行動の数。
Exploration vs Exploitation
探索と効用の矛盾の矛盾。
今のPolicyよりもよいものを見つけるには探索するしかないが、探索する間の損は仕方ないがしてしまうことになる。
-greedy戦略
の確率でランダムなアクションを取り、それ以外は今わかっているとなる行動をとること。
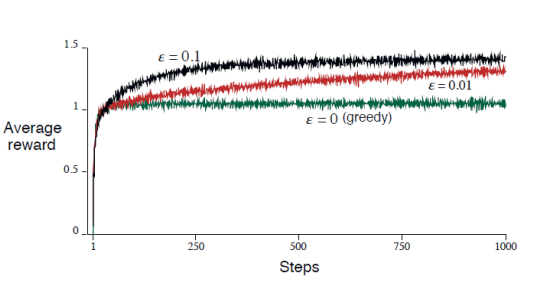
このように、単純なGreedyだけでは最大の利益を得ることはできない。
Upper Confidence Bound(UCB)
取るActionを以下のようにする。ここで、は、価値推定の不確かさを表す関数であり、不確かであるほど高い値を取るように。は定数。
つまり不確かであるうちはどんどん現時点での最適を取らずにチャレンジすることを促している。
Contextual Bandit Problem
モデルが以下のように、中身パラメタがあるときにはパラメタを推定しながら、最適のポリシー選択にもそれを選択するということ。
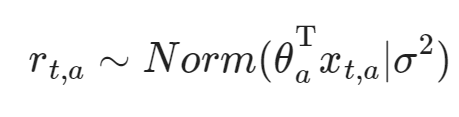
流れとしては以下の通り。
- それぞれのBandit Machineはガウス過程回帰に従うとする(以上のようであるということ)
- 期待値と分散を推定する。
- ポリシーに従って、アクションを決定
- 報酬と新しい環境を得て、1番に戻って再度推定する。
ベイズ最適化
観測データは真の値に、ガウス分布に従うノイズが加算されたものとする。これを多項式回帰で計算し、二乗誤差を損失とする。
この時、データ全体が従うのは、
の分布であり、これの対数尤度の最大化はに実質相当するのでそう言える。
ベイズ最適化は、データが従う事前分布=これがこういう動きになるとすでに知っていることが前提。これに対して、尤度と分布を学習によって覚えることで、事後分布を得るのが目的。
目的関数が不明である中で、その目的関数を最大化するための最適なパラメタを推定したい。気持ちとしては、以下のような帯があって不明な形の関数について、不確定性を織り込んでも、一番最大の値を引くにはどのなのかを知りたい。
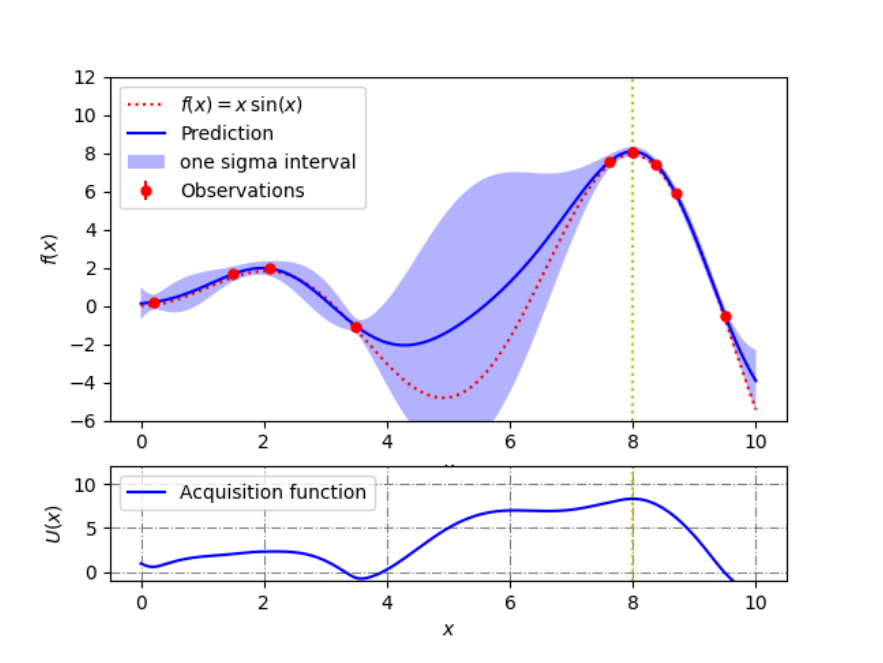
ここでいうAcquisition Function=獲得関数とは、予測したものに標準偏差を足したもので、上のグラフでいう色つきの帯の一番高いところを知りたい。
この時以下の手順を踏む。
- ガウス過程回帰(先ほど言ったデータ全体がガウス分布に従うというもの)で強化学習の目的関数を推定する。
- 獲得関数を最大化する
- パラメタを代入して計算する。
これを繰り返す。
各個を解説する。
ガウス過程回帰
関数がガウス過程に従うとする。以下のように、期待値と共分散行列に従うとする。期待値と共分散行列はいずれもの関数である。共分散関数は任意の2点の共分散の度合いを表しており、高いと2点が密接に関連しており、片方がわかるともう片方の値を推測しやすいことを表す。
1次元における標準偏差が大きいとデータが散らばるとはまた別の概念。
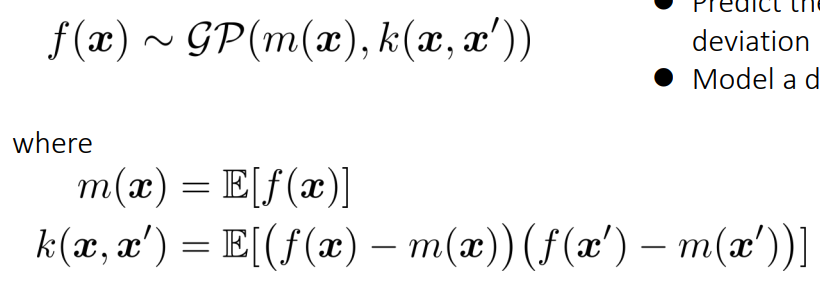
獲得関数の最大化
ここでは、を最大化するのではなく、ある獲得関数を最大化するを欲しい。
獲得関数の候補として以下のようなものがある。
- Upper Confidence Bound(UCB) は定数
- Expected Improvement(EI)

どのように予測点での分散を計算するの
ところで、共分散関数から、仮ににおける標準偏差を得たい。(でデータをサンプリングしたことはない)
すでに個の点を持つとき、新しい点とそれらの共分散ベクトルは以下のようになる。
これで、を計算すると、以下のようになる。
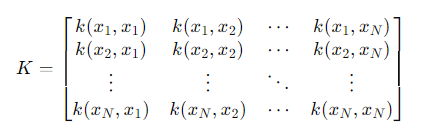
新しい点での予測分散は、以下のようになる。標準偏差は√をとればいい。
獲得関数の最大値を知りたい!
非常に簡単だが有効な手法として、Cross Entropy Methodがある。
- 今あるポリシーに従い、サンプルを集める。
- 低い報酬のサンプルを除外していく。=Elite Sample
- ポリシーを、残ったサンプル=Elite Sampleの報酬の和を最大化するポリシーとして訓練し、更新する。
強化学習の種類
Model-free, Model-based
参考: https://kiyosucyberclub.web.fc2.com/OpenAI_Gym/Gym02-02.html
強化学習にモデルがあって、それにパラメタを当てはめることによって、次のポリシーを自ずと決めることができる=Model based。これは決定的である。
つまり、状態遷移確率と遷移の報酬がわかっているときはModel Based。それ以外はModel Freeらしい。
しかし世の中の事象はキレイにモデリングできるものばかりではない。モデルが存在しない=Model freeのもの。今まで述べてきたQ-lerningとかもこれ。
Policy-Gradient-Free & Policy-Gradient-Based
ポリシーのについて、以下のように更新していくのが、Policy Gradient Free(Gradientを使わない)
最適化にGradientを使って勾配降下法をやるのが、Policy Gradient Basedである。
Episode-based & Step-based
Episode-basedは、最初にパラメタを生成し、そのを未来永劫使って今後のアクション決定をする=最初で実質アクションを全部決める。のようにサンプリングして。最初の決定1つで全部決まるので、道程の中では全く意味不明な決定とはいえるんでブラックボックスでの最適化と言える。
Step-basedは既存のやり方で、1ステップずつ今のポリシーに従って、状態からどのアクションを取ればいいのかを決定する形。
proMP
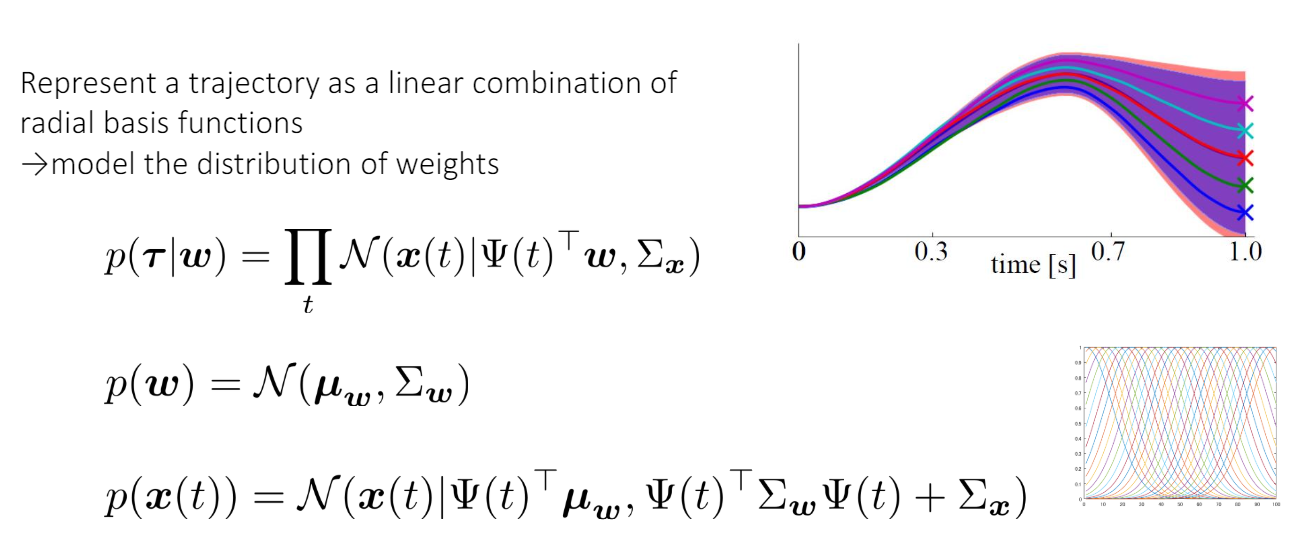
正規分布に従う重みと放射基底関数のベクトル(各既定関数が各成分になっている)を乗じたものが軌跡(の期待値)となる。ベイズ統計的に、不確定性を取り込んでいるので軌道はユニークではない。一番下のものは正規分布の合成によって得られた結果。
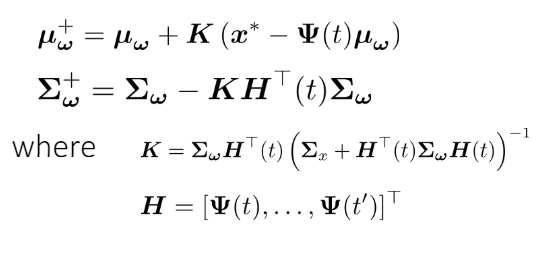
このように更新しているかな?
DMP(Dynamic Movement Primitive)

このように、加速度はゴールまでの向きから今の速度を減らし、そこに非線形の項にあたるものを加える。

非線形項では、softmaxのと、温度?を導入して、それを線形合成している。ゴールに近くなると、は0に近くなるようにしている(収束への保証っぽい)
On-Policy & Off-Policy
On-Policyとは以下のようなものである。
- 今集めているデータからわかる状況で、次のアクションを決定する。
- 決めたアクションをもとに、データを収集する。
つまり今まで通り。
これとくらべて、Off-Policyは以下のようなもの。
- 今集めているデータからわかる状況で、次のアクションを決定する。
- データ収集をするのは、ではなく、別のというBehavior Policy。
これによると、
- がわかっているとき、ポリシーがわかっていれば期待値が求まるらしい。これがOn-policy。
- 逆に価値関数を学習できないのならば、Off-policy。
Online RL & Offline RL
Online RLは今までのやり方の通り、その場で環境からフィードバックがもらえるというもの。
Offline RLは、学習できるデータが限られている(過去に集めたデータだけ)中で、どのように強化学習をしていくのかというもの。
2020年以降から流行り始めた。

