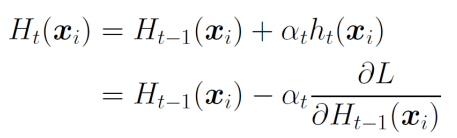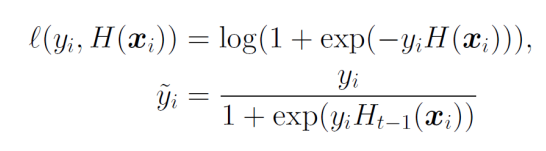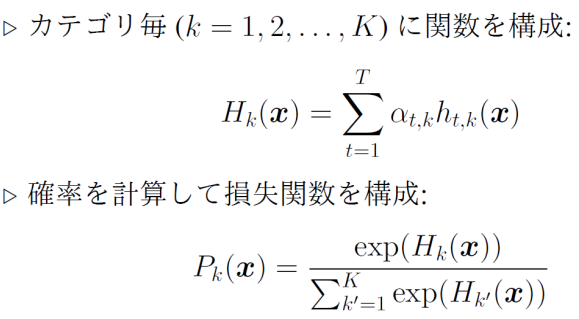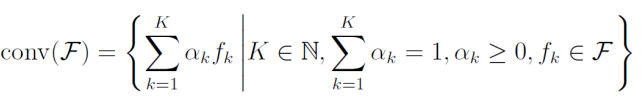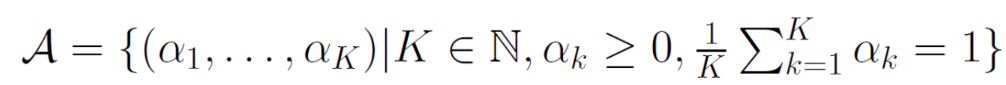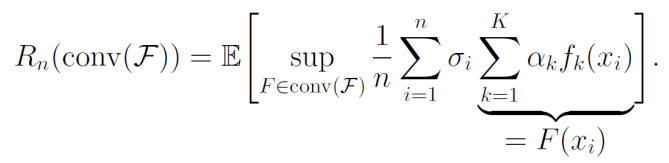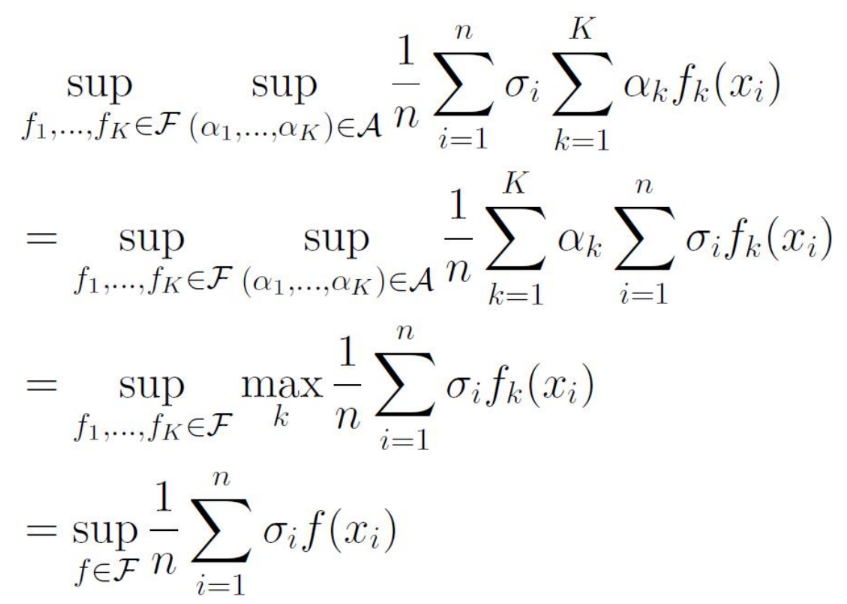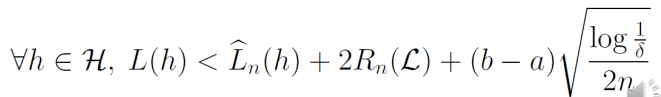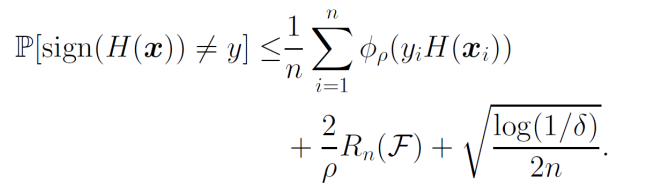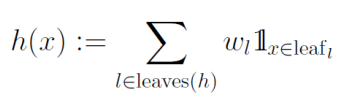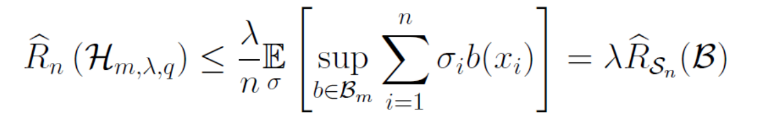Sen(Qian)’s Memo

前回はこちら。📄(講義ノート)統計的機械学習第8回 。内容は以下の通り。

これはよくない上界であり、よりよい上界の評価だと、$1-\delta$以上の確率で以下のようになる。

今回は、そこまで効率的ではないアルゴリズムであっても、数を集めるとうまく学習できるというBoostingについてである。

Probability Approximately Correct learning=PAC学習というものがある。

ある真の仮説$h^*$がPAC学習可能であるとは、$\forall \epsilon, \forall \delta$について、以下を満たす仮説$h$を出力する多項式時間アルゴリズムが存在すること。

うまく仮説を見つける多項式アルゴリズムがあればOK。

まず、弱学習器について定義する。

先ほどのPAC学習で$\forall \epsilon, \forall \delta$で成立するということだった。これを$\exist \epsilon. \exist \delta$という、ある固定された2つの値で学習できる学習器のことである。

この弱学習器があるなら、PAC学習可能な学習器はできるか？→できます！

複数の識別器による重み付き(もちろんすべて重みが同じでもいい)の識別器による多数決をするアルゴリズムであること。

線形で分離不能であるとしても、多数決のシステムを導入すれば非線形も学ぶことができる。

• バギング　$t$個目の識別器の訓練に使うデータは、全体のデータ$D$からサンプリングして選ぶ。
• ブースティング　$t$個目の識別器の訓練に使うデータは、全体のデータ$D$だけではなく、今までの識別器$f_1, \cdots, f_{t-1}$を参考にして作る。

📄NNDL 第9章 教師なし学習 も参考にする。

回帰について考える。

• 観測データ$\{ (\mathbf{x}_i, y_i) \}_{i=1}^n$である。
• 弱識別器は$h: X \to \mathbb{R}$

集団学習における回帰問題は、以下のように重み$\alpha_t$を割り当てて、弱学習器$h_t$を選ぶ。ではどう決めるのか？

弱学習器を追加するときに、追加した結果できるだけ$y_i$に近づいてほしい。

よって、次の弱学習器は、残差$y_i - H_{t-1}(\mathbf{x}_i)$を学習するようにすればいい。

学習器$H_{t-1}$について損失関数を以下のように、MSEによる回帰の形にする。

ここで、$\mathbf{x}_i$を固定して微分を考えると、以下のようになる。

ここで、以下のような$h_t$を選ぶとする。

そうすると、$H_t(\mathbf{x}_i) = H_{t-1}(\mathbf{x}_i) + \alpha_t h_t(\mathbf{x}_i)$へ代入をしてみると、以下のようにまさに勾配法になる。

なので、1ステップ前の関数で勾配法を適用させることで、自動的に残差を学習できる。

逆に言えば、$h_t$がわかれば、それがGradientの負符号になる。実際はそこまで理想的な$h_t$を得ることはできないので以下のように計算される。

なので、具体的には以下のようになる。損失関数が2乗誤差である必要がなく、2乗誤差であれば微分したらちょうど残差になりより数学的には推定の精度が上がるというだけである。

1. 損失に対して、$H_{t-1}$についての勾配を計算する。

1. その勾配$\tilde{y}_i$にできるだけフィッティングするような関数を探す。$y-H_{t-1}(\mathbf{x}_i)$は残差であり、MSEを使うならば今探している$h(\mathbf{x}_i)$はその解である。

1. 更新するstep sizeを計算する。これは一意に決められる。

1. $H_t = H_{t-1} + \alpha_t h_t$で更新する。

二乗損失では、微分すると残差になる。

絶対損失では、劣微分すると$\tilde{y}_i = \mathrm{sign}(y_i - H_{t-1}(\mathbf{x}_i))$となる。つまり残差の符号になる。

ロジスティック損失では、以下のようになる。

これは回帰についての手法なので、分類に適用するときは以下のようにする必要がある。

カテゴリごとに、所属している=0、所属していない=1を予測するように(onehotの予測のように)する。

それか、softmax化させたものを損失関数で予測する。

まず、凸包を定義する。これは該当の$k$個の仮説について重みを割り当て、その重みの和が1になるようなときに作った識別器の集合のこと。

凸包のRademacher複雑度は、もともとのRademacher複雑度と等しい。

証明はこちら

まず、次のような集合を考える。

このような集合を考える。これを重みに用いて、以下のようにRademacher複雑度で展開できる。

ここでの$\sup$の$\mathrm{conv}(\mathcal{F})$をかきかえることができる。$\sup _{(\alpha_1, \cdots) \in \mathcal{A}} \sup_{(f_1, \cdots) \in \mathcal{F}}$となる。

このように、$\sigma_i, \alpha_i$の順序を交換してみると、$\sup_{\alpha}$は一番大きい所だけ$\alpha_i=1,$それ以外は0にすればよく、それはつまりmaxを取るのと変わらない。

この操作をすれば、おのずと当初のRademacher複雑度$R_n(\mathcal{F})$が得られる。

弱学習器の集合を$\mathcal{F}$とする。Boostingの仮説関数$H(\mathbf{x}) = \sum_{t=1}^T \alpha_t h_t(\mathbf{x})$として、その集合を$\mathcal{H}$とする。

ここでは$\alpha_t$の非負、和が1を満たす必要がある。Boostingによってはそうじゃないものもあるので、もし重みが負ならば$\forall h, -h \in \mathcal{F}$とすればいい。和自体は正規化してもいいので正規化する。

Rademacher複雑度による汎化誤差解析は以下のようになっていた。

これを利用すると、以下のようになる。

$\forall \rho > 0$に対して、$1 - \delta$以上の確率で以下が成り立つ。

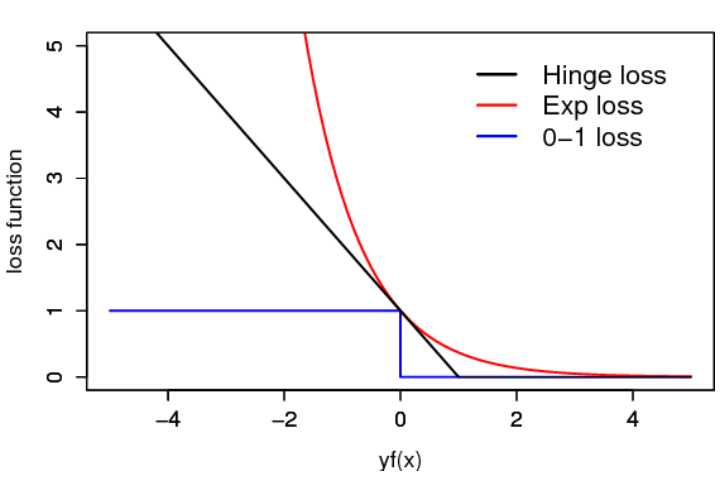
ここで、$\phi_{\rho=1}(y_i H(\mathbf{x}_i)) \leq \exp(-y_i H(\mathbf{x}_i))$を用いれば、AdaBoostの汎化誤差解析ができる。ここで使っている$-\exp$は非常に誤差に対して厳しいものである。

これの証明自体はほぼ自明であるので、書かない。Taraglandの補題と、01損失を$\phi_{\rho=1}$を使って上から押さえられるというのを使う。

仮説関数は、ある閾値$z$を引いた時の符号に$\alpha=+1,-1$を乗じたもので、これは弱識別器である。そして、$k$クラス分類であるので、識別器は$d, k \in [1,d]$個ありその中での最大値を取るクラスを識別結果とする。

形からして、Massartの有限仮説の補題を使いそう。

まず、$\mathcal{H}$は$z$が無限に値をとれるので無限集合のように見える。しかし、$\alpha, d$は有限であり、各データ点は有限であるので、取りうる意味がある$z$は高々意味のある$n+1$通りしかない。なので、実は$\mathcal{H}$は有限集合であり、以下のMassartの有限仮説の補題を使える。

そして、$|\mathcal{H}| = 2 \times d \times (n+1)$であり、取りうるデータ点が$|M|=1$であるとすれば、示せた。

テーブルデータに強い。

回帰木と呼ばれる実数値を出力する木のアンサンブルをする。

回帰木は$+1,-1$に限らず、連続値を出力する。

Gradient Boostingのアルゴリズムに落とし込んで考えると、

こんな風にやりたい。ここにある$h(\mathbf{x}_i)$は回帰木である。

まずは回帰木について定義する。

各葉$leaf_l$は値$w_l$を持つ。入力$\mathbf{x}$を、葉のいずれかに対応付けるノード分割関数(左に行くか右に行くかのように)を決定木で実装する。

そして、葉の出力については、入力$\mathbf{x}$が分類の末にたどり着いた葉$leaf_l$に入っているなら1、入っていないなら0を得るようなもの$\mathbf{1}[\mathbf{x} \in leaf_l]$を考える。

回帰木は、以下のように定義できる。所属している葉は1つしかないが、これを指示関数で表現し$w_l$の重みを乗じている。

回帰木を構成するすべての葉について、すべてに重みを割り当てて帰ってくる値はそのうちの1つの$\mathbf{x}$が行き着いた葉ということ。

$\mathbf{1}$の総和は1つだけ1になるが、それについてRademacher変数を割り当てて考えてみる。つまり、以下のようになる。これらを成分としたRademacher変数のベクトル$\boldsymbol{\sigma}$があるとする。つまり、重み

回帰木のノルムについて、正則化の制限をする。$q \leq 1, ||\mathbf{w}||_q \leq \lambda$である。

そして、$h(\mathbf{x})$のノード数(同じ葉の数でも、それに至るまでの条件分岐=ノードの数が違うかも)を$m$とする。これらを変数として、決定木の集合$\mathcal{H}_{m, \lambda, q}$を定められる。

これからRademacher複雑度を計算していく。

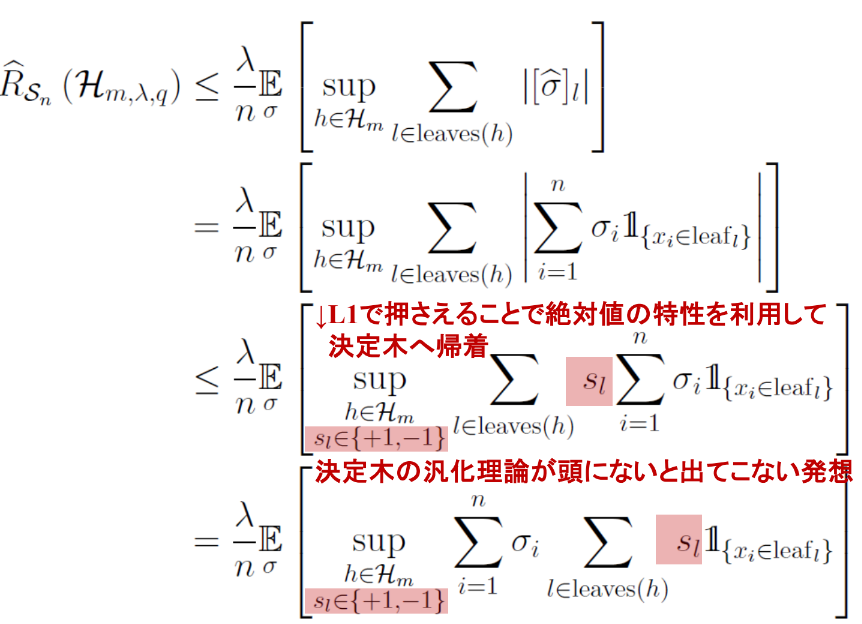
まず重み$\mathbf{w}$とRademacher変数と枝を掛け合わせた$\boldsymbol \sigma$の内積に分解でき、次にHolderの不等式で内積を$r,q, 1/r+1/q=1$のノルムに分解できる。

そのためにノルムの仮定を設けたのであり、次に$r$ノルム単品はL1ノルムで抑えられる。

なぜL1ノルムで評価したのかというと、回帰木のRademacher複雑度の絶対値を外したい。絶対値を外したい=絶対値の外に$-1,+1$を取る変数を入れて、それのsupを取る事に当たる！(Rademacher変数も$-1,+1$を取るがあちらはランダム。これは恣意的に選べる。)

このように$s_l$を導入できるには意味があって、最後の式変形のように総和の交換を行うことで、重みが恣意的に動かせる$\mathbf{w}$である回帰木ではなく、重みが+1か-1であり、($\mathbf{1}[]$は1つだけ1となり他は0となる。1のところの$s_l$だけを出力する)決定木となる。

よって、これの集合を以下のようにすると、また式変形ができる。

このように、$s_l \in \mathcal{S}_n$のRademacher複雑度に帰着できる。ノード数が$m$の二分決定木であると仮定する(そうじゃなくてlogに入れる都合上関係なさそう)と、そのような決定木の集合$\mathcal{B}_m$の集合は有限である(前述のように、学習データが有限なので、意味がある決定木の数が有限ということ)

なので、Massartの有限仮説の補題から、抑えられる。

回帰木を決定木に帰着したい、ということなのでL1ノルムで抑えたという形。

出来るだけきれいに分かれてる二分木である決定木のモデルを考える。

深さが$D$の時、葉の数は$2^D$であり、それに至るまでのノード数は$1+2+4+\cdots=2^D-1$である。

ノードの閾値を$\theta=0$を固定し、各ノードの選択に使える特徴量の種類が$d$個であるとき、二分木全体のサイズは

今は閾値が全部で統一しているが、閾値を自由に動かせる場合はどうか？無限に動かせるが、実質意味がある閾値はデータ点$n$個を分類するために$n+1$個しかないので、以下のようにサイズを抑えられる。