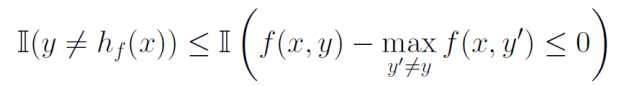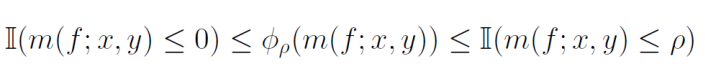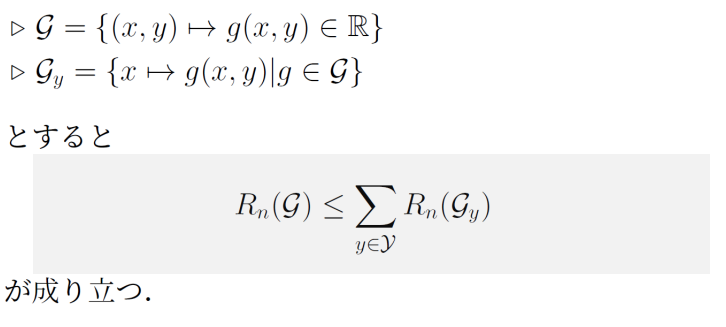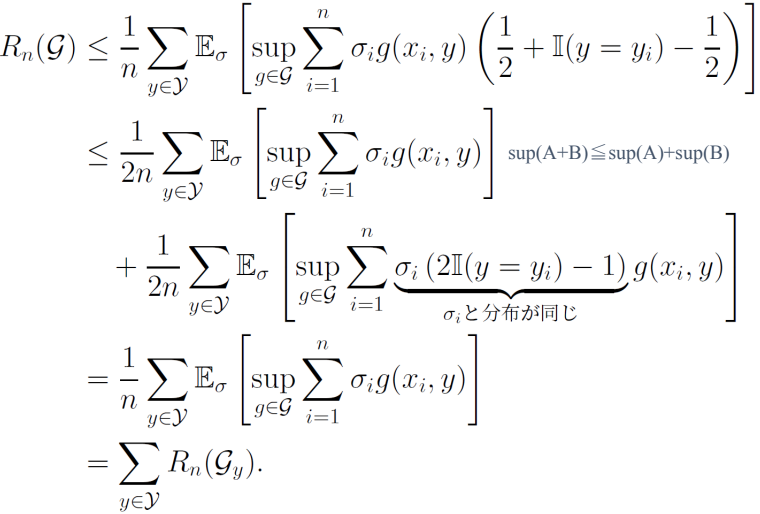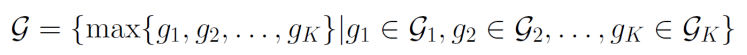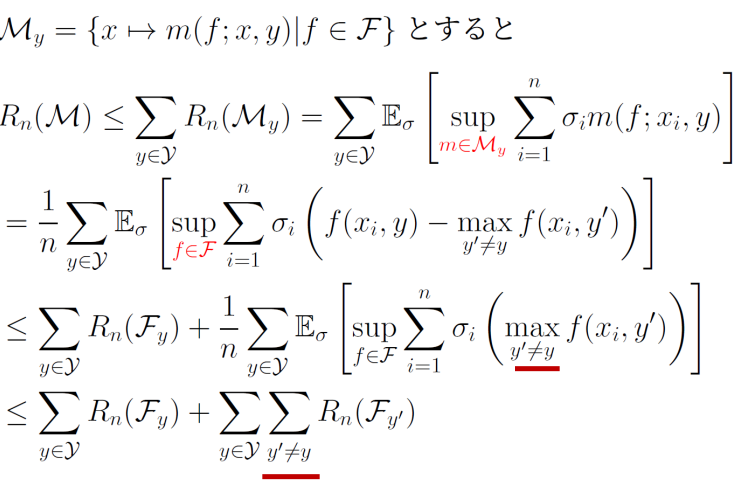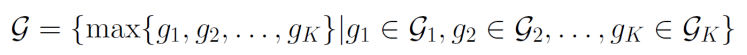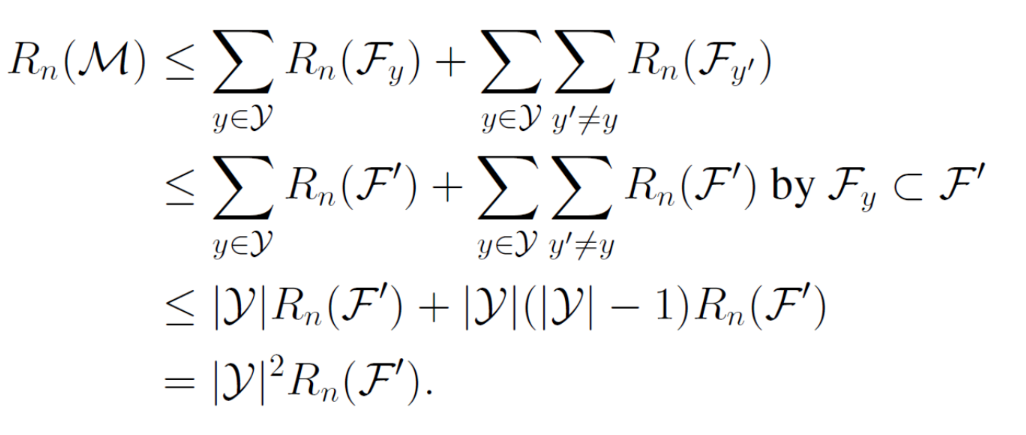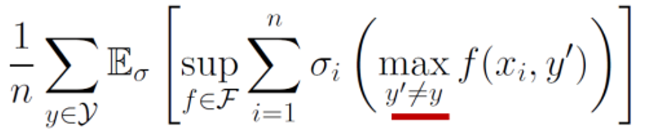Sen(Qian)’s Memo

前回はこちら。📄(講義ノート)統計的機械学習第7回 。内容は以下の通り。

2クラスの定義は以下のようになっている。

そして、二値分類で、ヒンジ損失$l((\mathbf{x}, y), h) = \max(0, 1 - y f(\mathbf{x}))$を使ったとき、リプシッツ定数は1であることから、損失関数のクラスのRademacher複雑度は以下のようになった。

📄NNDL 第3章 線形学習 ここでも書いてある通り、出力は$K$クラスなので、$\{1, \cdots. K \}$とする。関数$f$ではクラス$y$にあたる重みベクトル$\mathbf{w}_y$を持ってきて、内積を得る。そして、仮説関数はすべてのクラスの間で計算した内積で最大の値をとる。

つまり、重みベクトルをすべてまとめるとｍ、$W \in d \times K$となる。入力の次元は$\mathbf{x} \in \mathbb{R}^d$である。

多クラス分類のマージンは以下のように定義する。当該クラス以外のクラスの中で最も高いスコアを引く。これが正ならば当該クラスが判定結果であり、正ではないならば当該クラスではない。

そして、以下のように、ラベルが合わないというのは上の指示関数が成り立つ。

マージンが正ならば、正解を分類できて、負ならば誤った分類をしたということになる。これについて、マージンに対しての損失$\phi_\rho$を考えることができ、以下のように経験的なマージン損失を計算もできる。

これらについて、$\phi_\rho$損失は以下のように抑えられる。傾きが$\rho$のRamp損失を階段関数で抑えている感じ。

そして、マージンの集合を以下のように定義する。ある識別器$f$について、サンプル$\mathbf{x}_i$とラベル$y$の差=マージンを得るような関数の集合。

また、次の関数の集合を定義する。通常の$f : \mathcal{X} \times \mathcal{Y} \to \mathbb{R}$だけではなく、任意の指定のクラス$y^\prime$についてのスコアを得ることができるので、$\mathcal{F} ^ \prime$は$\mathbf{w}_1, \cdots, \mathbf{w}_K \in \mathbb{R}^d$の集合であると考えられる(与えられた正解ラベル$y$のみならず、任意の$y ^ \prime$についてスコアを計算するにはこういう技巧が必要)。

次にRademacher複雑度関連の準備をする。まず、以下のことが成り立つ。

• 上のものは、$\mathbf{x}, y$を受け取ったら$g(\mathbf{x}, y)$が返ってくるだけなので、識別器の仮説空間そのものである。
• 下のものは、クラス$y$を固定して、$\mathbf{x}$だけを入力として受け取る。

つまり、すべてのクラスについて出力しうる仮説空間のRademacher複雑度は、特定のクラスに限ったスコアを出力する仮説の集合のRademacher複雑度をすべてのクラスについて足したもの以下である。

具体的な証明はここにある。

Rademacher複雑度関連の式変形では、とにかく$\sum_i \sigma_i A$の形を作り、しかも$A$がベルヌーイ分布に従うRademacher変数を与えられたとき、それに反応して半々の確率で正解なら1不正解なら-1の値をとるのが大事。

そして、ここでは識別器については指示関数で賢い変形をしている。

そして、先ほど作り出した$1/2$を加算、減算した部分は$1/2$の加算だけくくりだして、減算した部分は$2 \mathbf{1}[y = y_i] - 1$になって、2クラス分類と同じように正解、不正解を+1, -1と値をとるようにすることができる。つまり、実は2つは同じものなので、最後に足し合わせたら、所要の形が出てきて示せる。

次のように、$\mathcal{G}_1, \mathcal{G}_2, \cdots$があるとする。この時、以下のようなことが成り立つ。$\mathcal{G}$は以下のように定義される。

一般的に、以下のようにmaxを書き換えられる。

これを使うと、絶対値関数が1-リプシッツ連続であることから、以下のようになる。

絶対値とRademacher複雑度は相性がよく、Rademacher変数を乗じると符号にかかわらずランダム化される。そして、$g_1, g_2$の総和に対してsupをとると考えると、最大値をとるので符号がどちらも和なのが一番大きい。

これを再帰的に適用すれば、$n$個までの和まででも成り立つといえる。

$m(f;x,y) = f(x, y) - \max_{y \neq y^\prime} f(x,y^\prime)$。該当クラス以外で最も確率が高いクラスとの差である。これを、以下のようにありうる仮説$\mathcal{F}$すべてに対して、ありうるデータからマージンを得る関数すべての集合。

次に、二値分類を多値分類に広げるため、以下のような仮説クラスを導く。これは二値分類から多値分類にただ広げているだけである。

この時、以下の式が成り立つ。実はこの上界はあまり良いものではないが・・・。

ここから証明を始める。

まず、$\mathcal{M}$を各クラスごとの$y$の経験Rademacherの和で上から押さえられる。

そして、$m$はマージンの関数なので、これを展開すると$\sup_{m \in \mathcal{M}_y}$から$\sup _{f \in \mathcal{F}}$にすることができる。

そして、$f(x_i, y)$の部分だけを単独で$\sup$つけることで、それ自体がRademacher複雑度であるゆえに出すことができる。そして残った第二項について、以下の準備その2を使う。

これによって、$\max$はunion boundのように抑えることができ、$y^\prime \neq y$である全てのものに対しての総和となる。

次に、総和を取られている$\mathcal{F}_{y^\prime}$についてだが、$\mathcal{F}^\prime$の定義は以下のようになっているため部分集合となっている。

よって、$\mathcal{F}_{y^\prime}$を$\mathcal{F}^\prime$に置き換えられる。

最後に、総和を$|\mathcal{Y}|$で抑えていくことによって、確かに$|\mathcal{Y}|^2$となる。

二乗となっている理由として、$R_n(\mathcal{F}^\prime)$の和が二重の総和であった。これを改善する証明は以下の通り。

もともとの式は、$1-\delta$以上の確率で以下の式が成り立っていた。

これについて、改良版では$1-\delta$以上の確率で以下の式が成り立つ。

クラス数の1乗の上界になっている。

$m(f;\mathbf{x}, y)$から、新たなに以下の$m(f;\theta;\mathbf{x}, y)$を、ある定数$\theta$を用いて定義する。

通常の定義では$y^\prime \neq y$という制約であったが、これを取り払う代わりに「一致していたときには$\theta$だけマージンに加算する」ということにする。これによって、選ばれた$y^\prime$が$y$と等しいときは正解の時は固定で$\theta$の値となり(今までは第二の候補との差であった)、それ以外の時は通常の$m(f;\mathbf{x}, y)$と同じようになる。

これについて、$m(f;\theta;\mathbf{x}, y )\leq m(f;\mathbf{x}, y)$が以下のように成り立つ。

この新たに定義したものを使って、損失関数$\Phi_\rho(\cdot)$を経由した経験損失との誤差は、同じ識別器に対しての経験誤差の評価なので、以下の式が$1-\delta$以上の確率で成り立つ。仮説集合から得られた$f$についての計算。

次に、$\Phi_\rho$について01損失で挟めることから、以下の等式が成り立つ。$m(f;\mathbf{x}, y) \geq m(f;\theta;\mathbf{x}, y)$であるので、0以下である確率は前者の方が小さくなる。

これを使って、先ほどの集中不等式を書き直すと左辺を以下のようにすることができる。

そしてここで、。$\theta = 2\rho$であると固定してみる。この時、以下のようになる。$y^\prime$が正解ではないときは$m(f;\mathbf{x}, y)$と等しく、正解であるときも$\Phi_\rho$はランプ損失であるので、$\rho$より大きい値では常に0をとることから以下の式が成り立つ。

$\theta=\rho$で固定しないのは、将来の式変形で$2 \mathbf{1}[\cdot]$の形を作れるとやりやすいから…?

(そのうえで、Talagrandの補題を使うことで、$\Phi_\rho$は$1/\rho$リプシッツ連続であるので、$R_n(\mathcal{\tilde{H}}^\prime) \leq \frac{1}{\rho} R_n(\mathcal{\tilde{H}})$が成り立ち、これで集中不等式を以下のように変形できる。

そして、$R_n(\tilde{\mathcal{H}}) \leq 2|\mathcal{Y}| R_n(\mathcal{F}^\prime)$が成り立てば、証明は終わることになる。

これについては、すでに示されている$R_n(\mathcal{G}) \leq \sum_{y} R_n(\mathcal{G}_y)$の証明と似た証明で示すことができる。

Rademacher複雑度の定義で展開して別々の項で考えることができる。

第一項はこの時、以下のように$\mathcal{Y}$についての和をわざわざ作り出してみる。

この目的は、$\mathbf{x}_i, y_i$の連動を消すことで、$\mathbf{x}_i$だけの関数にすればそれのRademacher複雑度が得られるからである。

すると、これは絶対値の外に出すことができる。

ラベルについての指示関数とRademacher変数の積は相性がよく、$\epsilon_i = 2\mathbf{1}[y=y_i] -1$とすれば、指示関数の$0,1$から$-1,1$と値をとるようになる。これを使って代入すると、以下のような形になる。

そして、Rademacher変数と乗じた$\sigma_i f(\mathbf{x}_i, y) \epsilon_i, \sigma_i f(\mathbf{x}_i, y)$の両方は、$\epsilon_i$は$+1,-1$のみをとるので($y_i$と関係なく)、同じ分布であることがわかる。

よって、あとは外の総和を分解することで、第一項は$|\mathcal{Y}| R_n(\mathcal{F}^\prime)$で上から押さえられる。

第二項については、第一項で$\sigma_i f(\cdot)$についてのRademacher複雑度を評価できたことから、すべての$y$の総和を計算すれば、同様に$|\mathcal{Y}|R_n(\mathcal{F}^\prime)$の上界を得られる。

第二項の残る$-2\rho \mathbf{1}[y=y_i]$については、指示関数が0の時は関係がなく、$y=y_i$の時も1というk定数となるので、Rademacher変数を乗じたときの期待値は0となる。

このように、指示関数とRademacher変数は、

1. $f(\cdot)$の予測結果に関係ない場合は定数なので、Rademacher変数を乗じても期待値を取れば0。
2. $f(\mathbf{x}, y)$の予測結果と連動する場合、

よって、すべてを評価したとき、右辺は$2|\mathcal{Y}| R_n(\mathcal{F}^\prime)$で抑えられて、当初の式を示せた。

この証明では、$\theta$を導入したマージン$m(f;\theta;\mathbf{x}, y)$を考えて、これを使って$m(f;\mathbf{x}, y)$を期待値で上から抑えている。そして、以下のように代わりのマージンのRademacher複雑度を考える。

これのRademacher複雑度では、同様に支持関数を作り出すことで一次の$|\mathcal{Y}|$で評価できた。

当初の証明では、以下のように別の$\mathcal{M}$で評価していた。

これについては、以下の部分の$\max$は総和となったので、$|\mathcal{Y}|^2$のオーダーとなっていた。

これについて、改善版では、いきなり全体に対して$\sum_{y \in \mathcal{Y}}$を$R_n(\mathcal{G}) \leq \sum_{i=1}^n R_n(\mathcal{G}_y)$から適用しておらず、第一項では適用させているが、第二項の部分では$\max$をそのまま総和に展開させている。これが、オーダーの上界を根本的に改善させている理由である。