https://papers.nips.cc/paper_files/paper/2019/hash/661c1c090ff5831a647202397c61d73c-Abstract.html
Introduction
線形識別器に比べて、ResNetの最適化における性質やRademacher複雑度などは先行研究では評価されていない。この論文では以下の部分を示した。
- 二乗損失を使うとき、あるデータ例において、全結合のNNは一番理想的な場合でも、線形識別器と同じかそれ以上の損失を招く。
- 複数の残差ブロックをつなげたDeep ResNetにおいて、一番最後の層は一番うまく学習できているが、必ずResNetのブロックの層が深くなるにつれてよく学習できていくというわけではない。
- Deep ResNetは2つの条件、Representation Coverage, Parameter Coverageを満たすのならば、以下の2点のいずれかの結果となる。
- たとえどんな局所最適解であっても、線形識別器よりは低い損失を招く。
- 少なくともHessianの固有値の1つは負である(ってことはやっぱり鞍点ってことじゃないですか)
- 2つの条件がなくても、示す式を緩めることで同様に示せる。
- Deep ResNetのRademacher複雑度の上界を得た。
Preliminaries
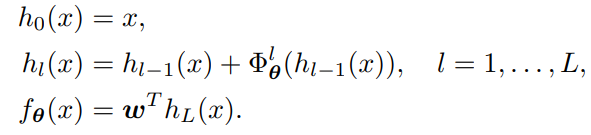
ResNetというのは残差接続で、入力がそのまま出力に足される。つまり、その間のネットワークは出力と入力の残差を予測するというもの。各ResNetブロックでは、入力と出力が微小な違いのみを持ち、それを細かく学習できる。そしてResNetブロックを重ねることで、微小な違いを複数回学習できるというわけである。
微小な違いのみを学習するので、深いネットでも勾配爆発や勾配消失が起きにくくなるし、ゆっくりとした学習ができる。
この論文においてのResNetは以上のように、任意の残差を予測するを用意し、最後には全結合層をつなげて1つの値を得るというものである。
Motivating Examples
3.1では、全結合層のすべての局所最適解が線形識別器よりも悪くなる実例を出している。
3.2では、各ResNetのブロックごとに出力の学習した表現と答えのの損失が以下のようになるというように感じられそうだが、その反例は存在する。
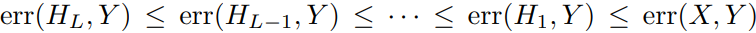
あくまで、層を重ねても最後の層のの損失はかならずより小さいということ。
Deep ResNetの局所最適解は線形識別器よりも良い
問題設定
以下のようにResNetを考える。1層目のブロックにおける残差計算では、入力に変換を加えずにに入れて、それ以降のブロックは入力に線形変換を適用させる。の計算が終わったら層関係なくで線形変換を施す。
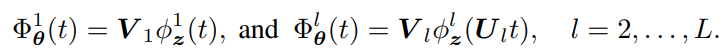
仮定として、損失関数は凸であり、2回微分可能であるとする。
定理2
以下の条件を満たすとき、
- Representation Coverage 損失の二回微分はスカラーなので、の外積がfull rankつまりが最大のを得るということである。
- これは最後の残差ブロックによる表現は空間をすべてカバーすることを要求している。最も損失関数が凸ならばこれは非常に緩い仮定らしい。
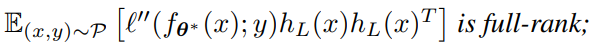
- Parameter Coverage パラメタの行列が空間をカバーしていないことを求めている。これはパラメタの行列は空間すべてを表現するだけの力がないということを示している。
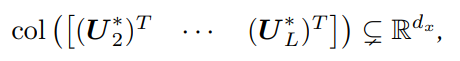
この時、以下のいずれかが成立する。
- 任意のResNetの局所最適解が線形識別器の損失よりも小さい。
- すべてのパラメタのHessianを考えたとき、必ず1つの固有値が負をとる。
- 固有値がすべて正ならば正定値で、その点では最小値をとる。
- すべてが負なら負定値で、その点では最大値をとる。
- それ以外=固有値が正だったり負だったり0だったり。これは鞍点。
先行研究では、以下のようなものを考えていた。
- スキップ接続
a→b, b→c, c→d, b→dのように途中の層から直接最後まで接続する。 - 並列ショートカット
a→b, b→c, c→d, d→e, e→f, b→f, c→f, d→fのように、Deep ResNetの各層があるとしても、その出力をすべて出力にそのままショートカットさせるというもの。
この論文の考えている単純にResNetのブロックを重ねるだけなのは初出。
ResNetの近似アイデンティティ領域における良性の特性
DeepResNetが層あるとき、残差ブロックを構成するのリプシッツ係数ががならば、Rademacher複雑度はネットワークの層の深さと各層の幅に依存しなくなる。
cirtical pointにおける誤差上界は省略。
ResNetのRademacher複雑度
先ほどの第1層だけに入れる前に線形変換をしないResNetではなく、以下のような画一的なResNetを考える。

定理5
データの集合があり、入力はと有界である。各層のResNetは以下のように、有界であるとする。

- 最後の線形のFCの重みのノルムは1以下。
- ResNetブロックにあるパラメタ行列のフロベニウスノルムは以下
この時、経験Rademacher複雑度は以下のように評価できる。
証明はこちら。
まずは隠れ層だけを表現するための関数空間を定義する。全結合層を外に出すために。
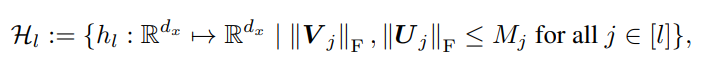
ならば写像に該当する。
この時、と書き直すことができる。
帰納的にやる。まずはという線形識別器であるので、これのRademacher複雑度は簡単に以下のようにわかる。
次に1層ResNetブロックを増やすことによる影響を考える。示したいのはである。
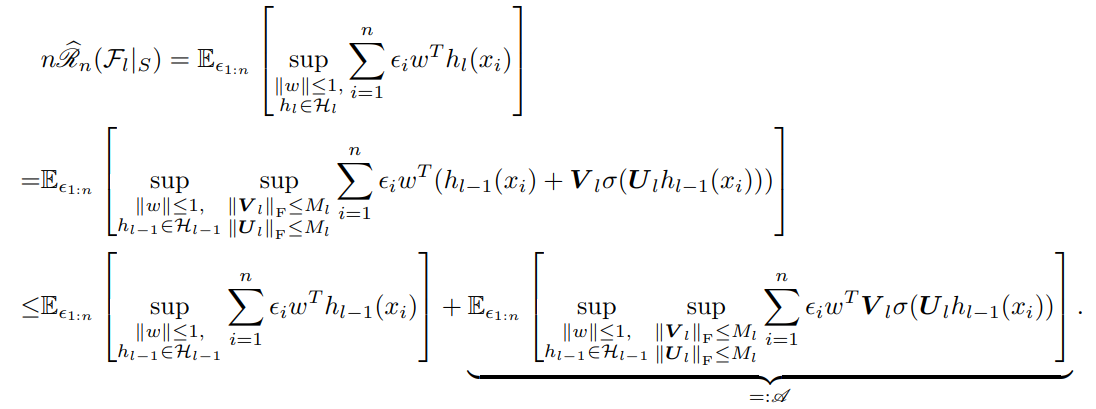
まずは倍したものを(を消したいので)定義通りに展開して、を再帰的にで表すようにすると、項を2つ分けることができる。前者の項は自明にであるので後者の項を考える。
まずは、についてとそれぞれ制限できるので、と行列のノルムからベクトルの2乗ノルムの上界に変換できる。そして、Holderの不等式により、内積を2乗ノルムどうし(2乗ノルムの双対ノルムも2乗ノルム)に以下のように変換できる。
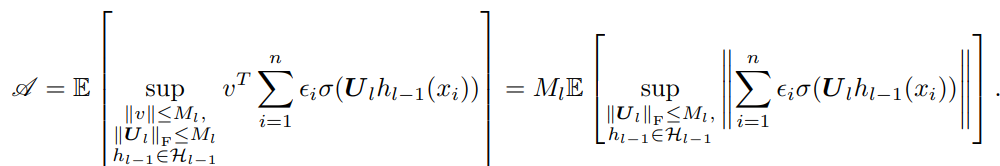
次に、この右辺を式変形していく。ここでは、はReLU関数であり、斉次性つまりが成り立つことから、式変形できる。
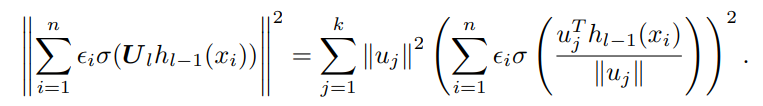
また、Rademacher複雑度で、を動かしたうえでのを計算するにあたり、で、それ以外のとするのが最善である。したがって、以下のような式変形が得られる。
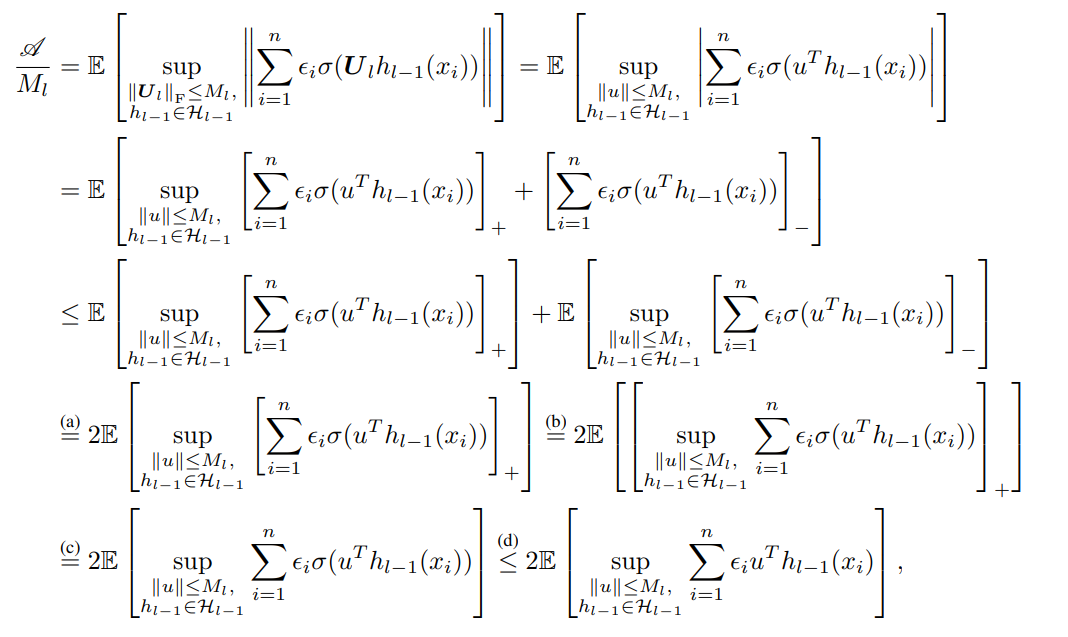
ここで、絶対値はリプシッツ係数を考察するうえで、とすると、と分解できることから、それぞれ式変形を行う。
そして、は変動する変数が許す限りは、符号が逆になったとしても変動する変数を動かすことで、結果的には同じような最大値を得ることができる。その後は、が適用できる範囲を広げることができ、結果としてを外すこととなった。
最後にのについて、式の中でのは一次であるので、外にをくくりだすことにより、と限定することができる。これはと考えてもよく(変数の名前を変えただけ)、結果として、以下のように、の係数が得られる。

結果として、以下の式が成り立ち、数学的帰納法により全体に帰着させることができる
