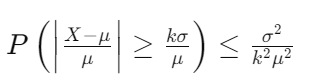(講義ノート)乱択アルゴリズム第6回

巨大すぎるグラフのは枝の数を推定することすら難しい。これを $|V|$ がわかっている状態で枝の数 $|E|$ を推定したい。

ただし、道具として以下の質問に答えられる、絶対に正しい機械=オラクルがある。以下で言うランダムは、一様分布に従ってサンプリングという意味。

平均次数を $\bar{d} = \sum_v d_v / n$ と計算できるが、これは全部計算するともちろん $2 |E| / |V|$ となる。このうまいこと平均次数を使いたい。

しかし、このまま仮定がなく $d_1, \cdots$ がランダムならば何もできない。

例えば、次数が正であるので、分散をまず見てみる。 $X_i$ は次数を表す確率変数。

V[X] = \mathbb{E}[X^2] - \mathbb{E}[X] ^ 2 = \frac{\sum_v d_v^2}{n} - \bar{d}^2

何回サンプルすればいいのか、というのを考えたい。そこで $|E|$ のオーダーを落としたうえで推定できないと困る。

チェビシェフの不等式 $Pr[|X - \mathbb{E}[X]| \geq k \sigma] \leq \frac{1}{k^2}$ の別の形である以下の式？を使うと、

右辺はさらに $V[X]/\mathbb{E}[X]^2$ 以下と $k$ を外した形にできる。これを代入して計算すると、 $\frac{1}{|E|} \frac{\sum_v d_v^2}{d^2}$ となるが、これは $\Omega(|E|)$ なので、よくない。

悪さをしているのは外れ値で、分散が大きいとどうにもならない。何とか推定する頂点の分散を小さくしたい…!

じゃあ分散を大きくするような外れ値はそもそも推定しなければいい。気持ちとしては、次数が大きすぎる頂点の次数を推定せず、小さいものをちゃんと推定する。外れ値を取り除くと言える。

まず、 $d_i$ を降順にソートする。この補題は、次数が多い $k$ 個の頂点の次数の和は、次数が低いものの総和と何かで抑えられるというもの。

$k$ 個の次数の多い頂点から出ている辺は、自分の中でクリークを作るのをのぞくと $k$ 個以外の頂点へつながるし、それは $\sum _{i > k} d_i$ で評価できる。なので、右辺にはクリークを作る場合と考えた ${}_kC_2$ を入れれば上界となる。

\forall k \in \epsilon [n], \sum_{i \leq k} d_i \leq \sum _{i > k} d_i + {}_kC_2

これを使うことで、以下のようにできる。

\bar{d} = \frac{\sum_{i \leq k} d_i}{|E|} + \frac{\sum_{i > k} d_i}{|E|} \\ \frac{1}{|E|} \sum_{i > k} d_i \leq \bar{d} \leq \frac{2}{n} \sum_{i > k}d_i + \frac{1}{n} {}_kC_2

ここで、 $k = \sqrt{\epsilon n \bar{d}}$ と選ぶと、エラー $\epsilon \bar{d}$ となるらしい。

ここで、 $Y = \sum_{j \leq t} X_j$ の解析を考える。

for i from 1 to t = O(\sqrt{n} / epsilon^2): 
	uを頂点集合Vからランダムにサンプリング。