Appendixもある版:
Introduction
既存のSemi-supervised Learningでは、データ分布の特定の分布に依存した手法で、Unlabeledデータに依存していた(低次元の多様体の上に分布してると仮定するなど)。既存の手法では、普通に訓練した結果を仮定に従って捻じ曲げいくことでいい性能を出してきた。しかし、仮定が間違っていたとなればより悪くなる可能性だってある。
そこに、近年Cost-sensitiveでPU Learningに対処する手法が開発されてきているので、これを用いたのがこの論文である。
Background
問題設定
- サンプルはx∈Rdであり、ラベルはy∈{+1,−1}の二値。
- Xp∼i.i.d.p(x∣y=+1)
- Xn∼i.i.d.p(x∣y=−1)
- Xu∼i.i.d.p(x)=πp(x∣y=+1)+(1−π)p(x∣y=−1)
- π=p(y=+1)でClass Prior。
- 損失関数lを設け、負の値を入れると損失が出るようにする。具体的な各学習の損失を以下のように定める。
真のリスク損失R(g)=Ex,y[l(yg(x))]となるが、真の分布を知らないのでこれをうまく分類する必要がある。
PN Classification
PN学習では、単純にπ=Pr(y=+1)、1−π=Pr(y=−1)とする。すると損失は以下のようになる。
RPN(g)=πRP(g)+(1−π)RN(g) ここで、損失関数lHをヒンジ損失とすれば、SVMでの対象の式になる。
PU Classification
π=Pr(y=+1)とすると、以下の式の最小化となる。
RPUNC(g)=2πRP(g)+EU[l(−g(x))]−π 先行研究によって、非凸関数の損失関数が望ましいとか、 📄 2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data 。
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data 。
凸関数のまま割り切って使うアプローチもある。これは以下の関数の最小化となる(式変形で上の形にできる)
RPUC(g)=πEP[l(−g(x))]+EU[l(−g(x))] 凸であると割り切って使ってもそこまで悪くない 📄 2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data という先行研究がある。
2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data という先行研究がある。
NU Classification
同様に式変形すると、以下のようになる。
RNUNC(g)=2(1−π)RN(g)+EU[l(g(x))]RNUC(g)=(1−π)EN[l(g(x))]+EU[l(g(x))] PN, PU, NUベースのSemi-supervised Classification
PUNU Classification
非常に簡単なアプローチで、Positive, Negative, Unlabeledを統合するには、あるγ∈[0,1]によって、以下のリスクを最小化すればいい。
RNC−PUNUγ(g)=γRPUNC(g)+(1−γ)RNUNC(g) これを展開すると以下のようになる。ここで、γ=1/2とすれば通常のPN学習と同じであることに注意(ちょうどEUの中身で打ち消し合うので)
しかし、Convexな損失関数を用いるときは、以下のような式になる。
ここで、γ=1/2ならば(1−γ)l(g(x))+γl(−g(x))はちょうど半々となり、これらの和は−g(x)になる。
このことから、γ<1/2の時、Negativeのクラスに対する損失がPositiveのものよりは小さくなり、γ>1/2ならばPositiveのクラスに対する損失が減る。
PNU Classification
単にPU+NUにするだけではない。今度はPN+PUとPN+NUをそれぞれ用意し、新たなパラメタによってその都度PN+PUを使うか、PN+NUを使うか、単純なPNを使うかを決める。
数式では、η∈[−1,+1]を導入して以下のような関数にしている。η=0はPNに相当で、η=+1はPNPU、η=−1はPNNUである。
導入することで、上のPNPU、PNNUについての統合した設計であると言える。
では、ConvexとNon-Convexのどちらが性能がいいのか?は実験で後述する。
実際の実装
今回の実装はカーネル法のSVMでやっており、パラメタの二乗正則化をしている。
minwwTΦ(x)+λwTw 理論解析
いつもの。
Generalization Error Bound
カーネル法で写像した先のヒルベルト空間は、重みや写像した先の関数に上界があるといういつもの仮定。
便宜のために以下のように書くとする。
Non-Convex
1−δ以上の確率で以下の3つの式が成り立つ。I(⋅)は01損失における期待値。Cw,ϕ,δ=2CwCϕ+2log(3/δ)
証明
まず、展開すると以下のような式になる。
このように展開した以上、RP(g),RN(g),RU,P(g),RU,N(g)について、それぞれ経験損失と理想損失の差(同じ識別器において)の上界で評価することができる。(📄 (講義ノート)統計的機械学習第2回 にあるようにLn(h^)−L(h∗)よりもこの形でやるとやりやすい)。それぞれ、1−δ/3以上の確率で成立する。
(講義ノート)統計的機械学習第2回 にあるようにLn(h^)−L(h∗)よりもこの形でやるとやりやすい)。それぞれ、1−δ/3以上の確率で成立する。
上の式はMcDirmidの不等式で評価している。あとはこれを代入することによって、以下の式が成り立つ。1−δ以上の確率で以下が成り立つ。(1−δ/3以上の確率で3つなら、(1−δ/3)3=1−δ+⋯で、後ろの省略した部分は正なので、成り立つ)
このように代入すれば、想定の式が得られる。
同様にこれらの式やればいい。
なお、この上の三つの式の経験損失はいずれも以下の速度で収束する。
Convex
RPUC(g)=πEP[l(−g(x))]+EU[l(−g(x))]RNUC(g)=(1−π)EN[l(g(x))]+EU[l(g(x))] Convexで使う式は以上のものである。これも同様に、リスク上界を評価できる。
証明
前と同じやり方で行ける。ただ、これは4つの項が出てくるので、1−δ/4以上の確率、というようにやる。
それぞれは、1−δ/4以上の確率で成り立つ。
同様に代入すればできる。
分散の減少
nU→∞とするとき、最大の?分散がどのように減っていくのかを評価する。次のように分散を定義する。
簡略化のために、以下のように書くとする。
ψP=π2σP2(g)/nPψN=(1−π)2σN2(g)/nN nU→∞の時、γを以下のように選べば、分散を最小化することができる。
いろいろあったけどひとまずスキップを…
PUNU vs PNUどっちがいいの
📄 2016-NIPS-Theoretical Comparisons of Positive-Unlabeled Learning against Positive-Negative Learning のように、誤差減少率の比をとってみる。
2016-NIPS-Theoretical Comparisons of Positive-Unlabeled Learning against Positive-Negative Learning のように、誤差減少率の比をとってみる。
αPU,PN=(θN/nN)θP/nP+1/nUαNU,PN=(θP/nP)θN/nN+1/nU 先行研究によれば、この比率が1より大きければ、PUよりPNのほうの上限が小さくなるということ。この時はPNで学習したほうがいい。逆に1より小さい場合はPUで学習したほうがいい。
同じように先行研究によれば、nUが少ないときはPNのほうが性能出るが、増えていくとPUかNUのほうが性能が出る。
PNU分類は巧みにηを選択するというものであり、PUとNUの良いほうをいいところどりできるらしい。しかし、PUNUは逆に悪い方を組み合わせている。
実用上、PUNUよりはPNUの方が優れているであろう。
実験
実際の分散削減
経験的なPNUリスクの分散がPNリスクの分散よりも小さくなるためにどれほどのUnlabeledのデータが必要なのか。
割と早い段階ですぐに分散は小さくなった。πが0.5から外れるほうがすぐに治作なる。これは先行研究 📄 2016-NIPS-Theoretical Comparisons of Positive-Unlabeled Learning against Positive-Negative Learning で実証されている通り。
2016-NIPS-Theoretical Comparisons of Positive-Unlabeled Learning against Positive-Negative Learning で実証されている通り。
検証におけるPNUリスク
経験的なPNUリスクは経験的なPNリスクよりも分散が小さいので、やはりUnlabeledを集められるときはPNをやってないで、PNUをやる方が実用上よくなることが多いのではないか。
比較実験
カーネル法のSVMを使ってやっていた。既存の研究にある16個のベンチマークテストと、画像分類(AlexNetの埋め込み表現を使って分類)を用いて実行した。
この手法が一番良かった。といってもPositiveもNegativeもUnlabeledも使う手法はこれだけなので、これがよかった!というのはちょっとずるい気もするが…
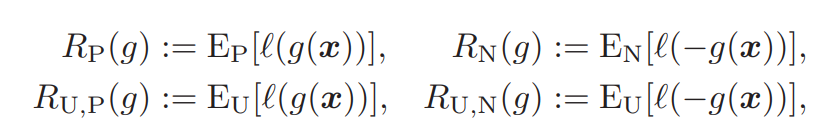
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data 。
2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data という先行研究がある。
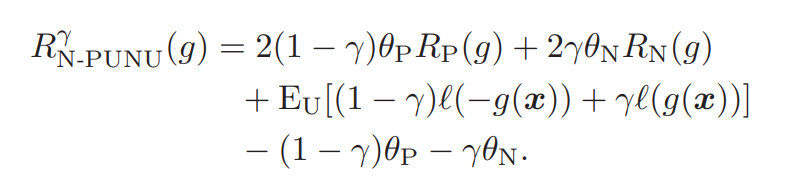

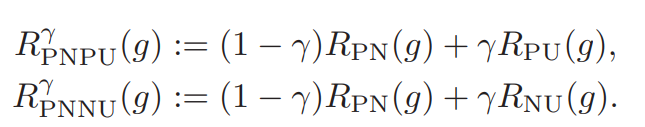
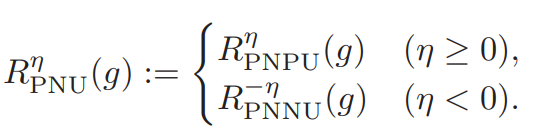

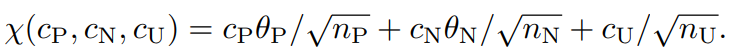
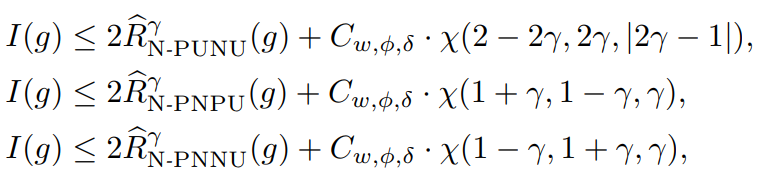
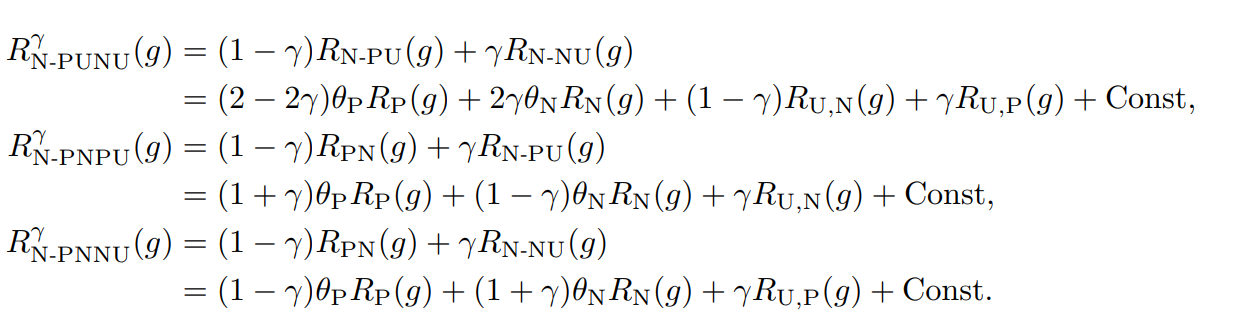
(講義ノート)統計的機械学習第2回 にあるようによりもこの形でやるとやりやすい)。それぞれ、以上の確率で成立する。
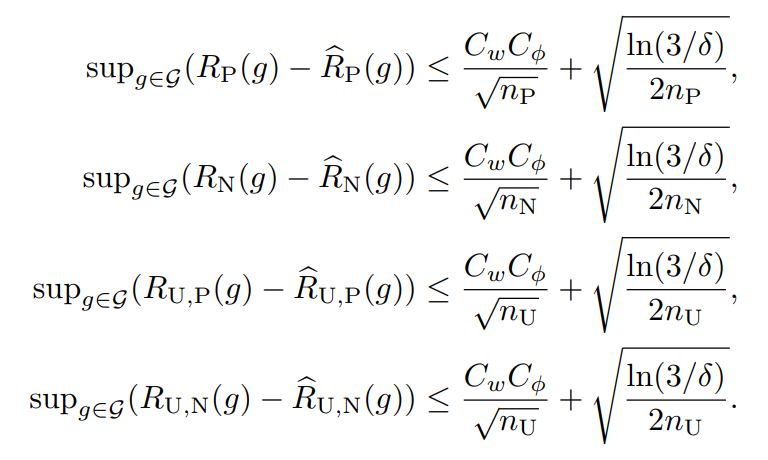
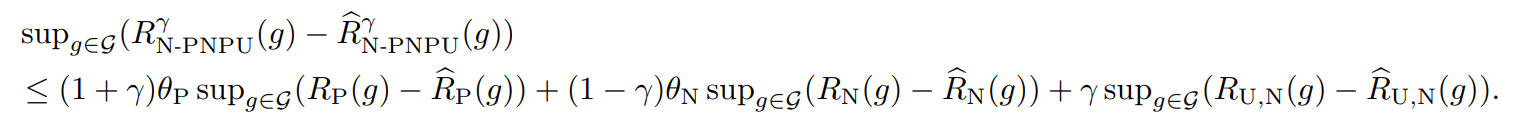
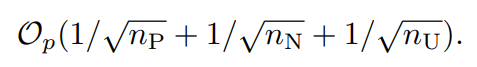
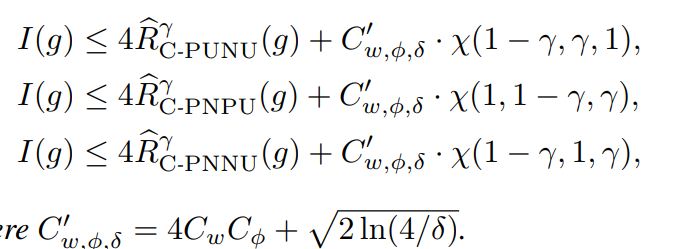
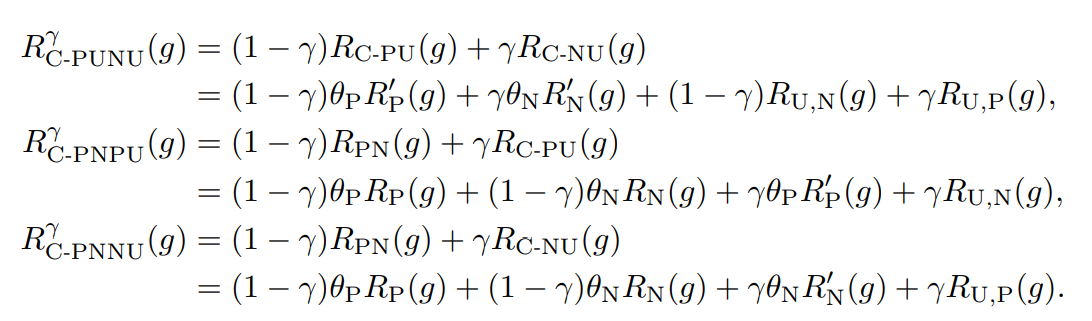
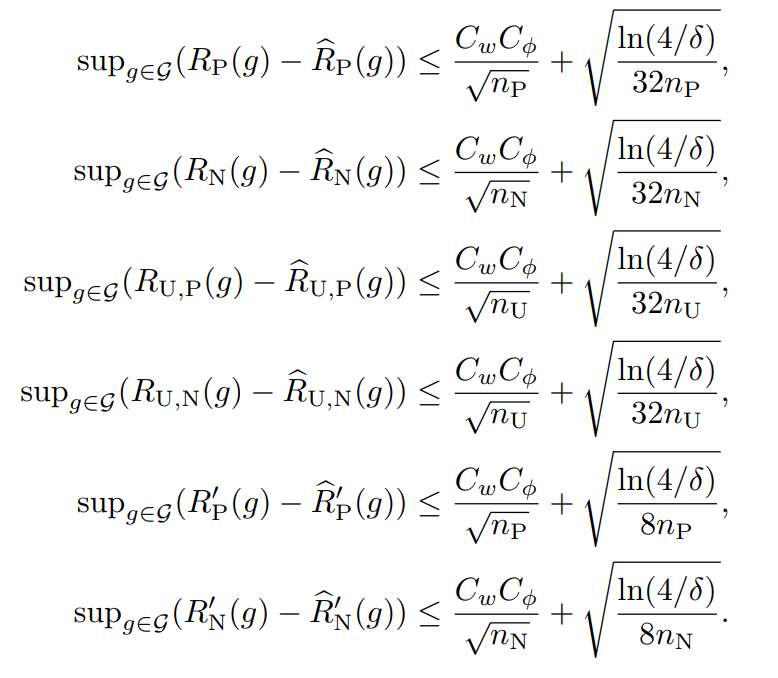
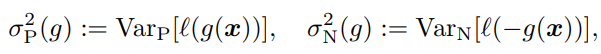
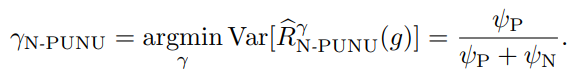
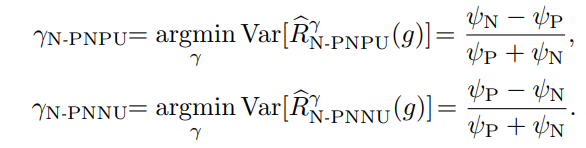
2016-NIPS-Theoretical Comparisons of Positive-Unlabeled Learning against Positive-Negative Learning のように、誤差減少率の比をとってみる。
2016-NIPS-Theoretical Comparisons of Positive-Unlabeled Learning against Positive-Negative Learning で実証されている通り。
