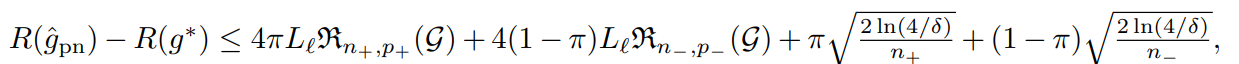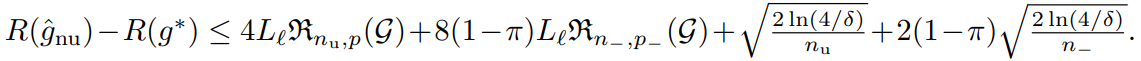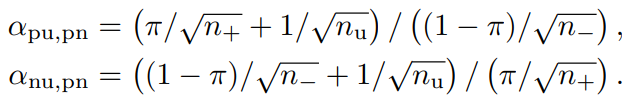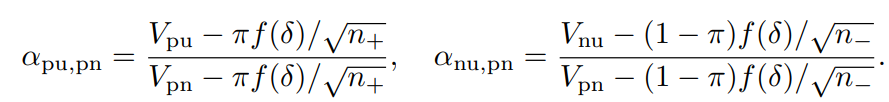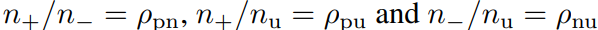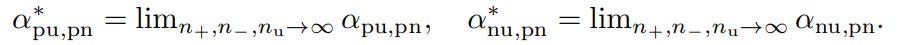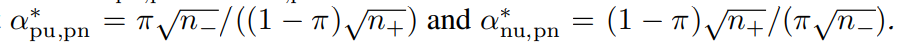https://arxiv.org/abs/1603.03130
Introduction
問題設定
X∈Rdがサンプルで、ラベルがY∈{+1.−1}である。シナリオはCase Controlである。つまり、p(s=+1)が得られないというもの。
📄 2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data では、代理損失が非凸で対称的であるなら、提案したものが不偏な分類器であると証明されている。ならば、普通のPNやNUの学習器と同様に比較できる。
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data では、代理損失が非凸で対称的であるなら、提案したものが不偏な分類器であると証明されている。ならば、普通のPNやNUの学習器と同様に比較できる。
リスクの不偏推定器
PNにおいての不偏推定器
p+(x)=p(x∣Y=+1),p−(x)=p(x∣Y=−1) g:Rd→Rを実数の決定関数として、これによって二値分類をしている。そしてl:R×{+1,−1}→Rをリプシッツ連続な損失関数だとする。
そして以下のようにリスクを定義する。それぞれp+,p−においての期待値である。
R+(g)=E+[l(g(X),+1)]R−(g)=E−[l(g(X),−1)] そして。PN Learningにおける全体の損失は、π=p(Y=+1)だとすると、以下のような式になる。一番下は不偏推定量での推定。
R(g)=πR+(g)+(1−π)R−(g)R^PN(g)=n+π∑x∈X+l(g(x),+1)+n−1−π∑x∈X−l(g(x),−1) 下の式は先行研究によって、O(1/n++1/n−)でR(g)に収束する不偏推定器であることがわかる。
PU, NUでの不偏推定器
PUではNegativeサンプルは手に入らないので、うまくR−(g)を書き換える必要がある。📄 2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data では書き換えの一種を提案し、対称的な損失は足すと定数になるので最適化しやすいという結果になった。
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data では書き換えの一種を提案し、対称的な損失は足すと定数になるので最適化しやすいという結果になった。
そこでは、以下のように書き換えることができ、目的関数を作れる(それをさらに分解すると対称的なものがいいとかの話になる)
EX[l(g(X),−1)]=πE+[l(g(X),−1)]+(1−π)R−(g)RPU(g)=2πR+(g)+RX(g)−πR^PU(g)=−π+n+2π∑x∈X+l(g(X),+1)+nX1∑x∈XXl(g(X),−1) 同様に、NUについても以下の式が得られる。
RNU(g)=2(1−π)R−(g)+RX(g)−(1−π)R^NU(g)=−(1−π)+n−2(1−π)∑x∈X−l(g(X),−1)+nX1∑x∈XXl(g(X),+1) 代理損失
01損失の代わりに、 📄 2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data ではScaled Ramp Lossを提案している。
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data ではScaled Ramp Lossを提案している。
lsr(t,y)=max(0,min(1,(1−ty)/2)) 当然だが、これはリプシッツ連続である。
リスク境界に基づいた理論的比較
- 識別器の所属クラスはGである。
- 真の最適の識別器はg∗である。
- PNで学習したときの真の識別器はg^pn=argmingR^pn(g)である。
- PUで学習したときの真の識別器はg^pu=argmingR^pu(g)である。
- NUで学習したときの真の識別器はg^nu=argmingR^nu(g)である。
- 代替損失関数lによる損失の最小化されたものは、R∗=infgR(g)である。
- 01損失関数lによる損失の最小化されたものは、I∗=infgI(g)である。
Rademacher複雑度の定義からして、所属クラスGのRademacher複雑度は定数CGによって抑えられる。qはPositiveデータ、Negativeデータ、PN両方のデータの分布みたいな感じ。
Rn,q(G)≤CG/n そして、以下のように、カーネル法を使うときの仮定を置いている。ヒルベルト空間Hを定義したら、写像した先の特徴空間もある定数で抑えられるとする。
カーネル法についての統計的機械学習で分析するときによくある手法。
Risk Bounds
同様に、ϕを広義単調増加かつϕ(0)=0であるならば、1−δ以上の確率で以下の式が成り立つ。
誤差上界としては、表現力が高いほど低く、かつ学習するデータが多いほどまた低くなる。
Rademacher複雑度を上から押さえる都合上、これらの上限の減るスピードはO(1/n+/n−)である。(Rademacher複雑度を抑えると同じルートになって、後ろのルートと同じオーダーになる)この速度で、Rの差は0へ、Iの差はϕ(R(g∗)−R∗)へ収束する。
証明の紹介
PUの式は以下のようになっている。
R(g)=2πR+(g)+RX(g)−πR^(g)=2πR^+(g)+R^X(g)−π これをもとにsupg∣R^pu(g)−R(g)∣を計算する。これは証明したい式から、統計的学習理論で上から評価するときに一番向いている形への変形である(同じgについてなので)。これは📄 (講義ノート)統計的機械学習第2回 📄
(講義ノート)統計的機械学習第2回 📄 (講義ノート)統計的機械学習第3,4回 にある通りである。まずここでPUにおける経験誤差と理想的なものに分解する。
(講義ノート)統計的機械学習第3,4回 にある通りである。まずここでPUにおける経験誤差と理想的なものに分解する。
、ここではMcDirmidの不等式で評価している。Llはリプシッツ定数(Talagrandの補題を使う)。
上では、1−δ/2以上の確率で、という条件であることに注意。
後はこの2つを合算させて、最後に📄 (講義ノート)統計的機械学習第2回 にあるようにsupにしたら1/2されるから2倍することで、証明は終わる。
(講義ノート)統計的機械学習第2回 にあるようにsupにしたら1/2されるから2倍することで、証明は終わる。
これはPUの式であった。これと同様に、PNもNUも、R(g)の合成の式から同様に、以下のように上界を導出することができる。
これをまとめると、各学習の収束速度は以下のようになる。
R(g^pn)−R(g∗)≤f(δ)⋅{π/n++(1−π)/n−}R(g^pu)−R(g∗)≤f(δ)⋅{2π/n++1/nu}R(g^nu)−R(g∗)≤f(δ)⋅{1/nu+2(1−π)/n−} 有限なサンプルでの比較
収束速度の比を考える。pnを基準に、pu, nuについて見る。
この時、αpu,pn<1なら、PNよりもPUのほうが収束が早い=いい性能が出る。
同様に、αnu,pn<1なら、NUよりもPUのほうが収束が早い=いい性能が出る。
上の収束速度一覧の右辺をVpu,Vnu.Vpnとすると、αはそれぞれ以下のように計算できる。
- pu,pnのほうではUnlabeledとNegativeによる上限の減少速度の比
- nu,pnのほうではUnlabeledとPositiveによる上限の減少速度の比
を比べている。
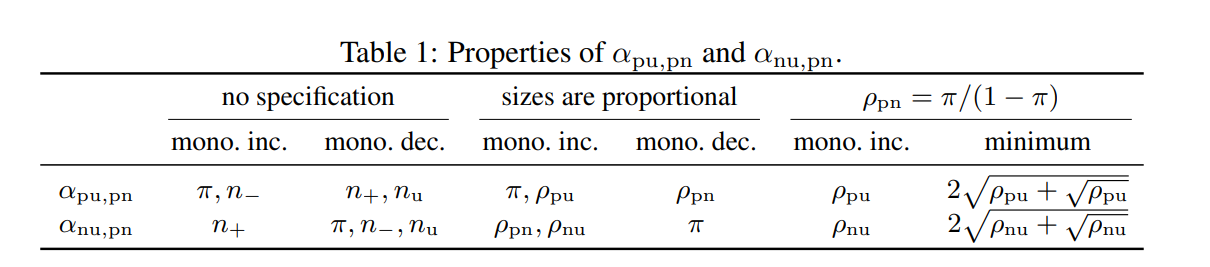
結論としては以下の表である。以下の表の変数が増加することによって、αがどうなるかがわかる。
n−が減る、そしてπが減るとαpu.pnは単調減少する。
PUではPositiveのデータは2πの重みがあるが、PNではπの重みである。よって、n+が増えるとPUのほうがPNより改善が早く結果的にαpu,pnが単調減少する。全体のサンプル数固定すると、n−がつまり減るということ。
πが増えると、PNでは(1−π)/n−の速度で減少する一方で、PUではO(π/N++1/nX)の速度で減少する。明らかにπが増えると、PNのほうが有益である。
結論として、PU学習ではπが小さいほうが望ましい識別器を作れる。
そのうえで、πによる比率を例えばPNで固定したときに、PUが増えるとどうなるか。これは表の2列目である。
表の三列目では、ρpn=n+/n−であるよりも、さらに強い(らしい)仮定であるρpn=π/(1−π)にしている。この条件下では、αpu,pnに以下のように下限をつくれる。
これは、π=ρpu/(2ρpu+1)の時に最小値をとる。
この式が意味するのは、nUが非常にn+に比べて大きいとき(ρPU<0.04の時など)ではじめて、αpu,pnは1未満となり、PUのほうの性能が上がる。
対称比較
実用上、PNのほうがPUより優れている、つまりラベル付きデータに比べてラベルなしデータの数が十分に多くないときが多い。この時、PU Learningをあきらめるべきか、もっとUnlabeledのデータを集めるべきか?
以上の極限をまず考える。これが収束するには、nUの増え方がnp,nnよりも早いことが必要である。
いっそのこと、nuだけ増えて他が変わらないとき、αは以下の値に収束する。
この時、この2つの値の積は1となるので、どちらかは1より小さいだろう。どちらも1であるときは、π2/(1−π)2である。この例外を除けば、Uが無限に取れるのならばPNやるよりはPUかNUやる方が効率がいいということ。
そして、いずれか一方が十分に小さければUnlabeledは少なくて済むかもしれないが、1に近ければUnlabeledは大量に必要だろう。それを集めるぐらいなら現実的にはPNをした方がいい場合もある。
Experiment
理論的な論文なので省略。予想通りの結果が出ましたということです。
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data では、代理損失が非凸で対称的であるなら、提案したものが不偏な分類器であると証明されている。ならば、普通のPNやNUの学習器と同様に比較できる。
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data では書き換えの一種を提案し、対称的な損失は足すと定数になるので最適化しやすいという結果になった。
2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data ではScaled Ramp Lossを提案している。
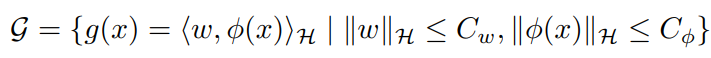
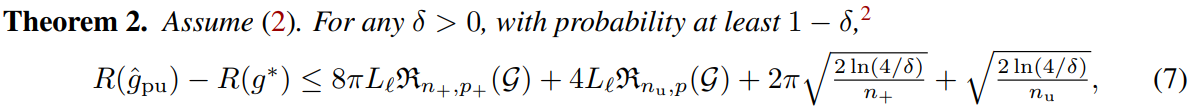
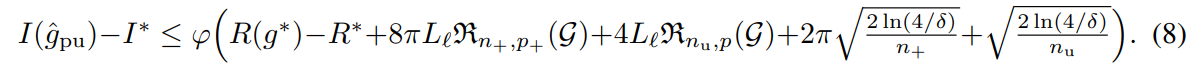
(講義ノート)統計的機械学習第2回 📄
(講義ノート)統計的機械学習第3,4回 にある通りである。まずここでPUにおける経験誤差と理想的なものに分解する。
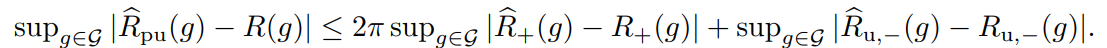
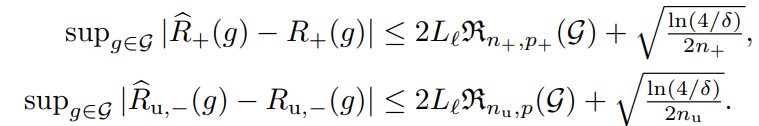
(講義ノート)統計的機械学習第2回 にあるようににしたら1/2されるから2倍することで、証明は終わる。