何がわかっていて何がわからない
入力に潜んでいる、潜在変数があるとする。からどのようにができるのかを知りたい。
- 既知。これは入力データの分布で、入力データから得られる経験分布を使う。
- ただし、詳細なモデルは当然知らない。
- 既知。人間ががどうなっているかを仮定する。
- 一般的にはとなる。
- 未知。一番知りたいもの。
- 直接知るのは難しいので、人間がモデルやそのパラメタを定めてを計算する。
- 未知。知ってると何かと役に立つもの。
- VAEなどの生成モデルでは、潜在変数から新たな例を生成するために必要。
変分推論とEMアルゴリズムの違い
EMアルゴリズムも、変分推論も結果的にELBOを最大化したい。
しかし、そのアプローチが異なる。
- 変分推論では、事後分布はモデルすらわからないので、人間があるモデルの分布を選んで、それで近似する。そのうえで、ELBOの最大化をする。
- 例えばDNNのような理論上任意の関数に近似できる学習器を使っても、変分推論のアプローチである限り変分推論。EMアルゴリズムではない。
- だがDNNで近似できると割り切れば別にEM Algorithmをやっても構わない。
- が厳密にわからない以上、我々はそれの近似分布のを動かしてELBOの最大化をするしかない。
- 例えばDNNのような理論上任意の関数に近似できる学習器を使っても、変分推論のアプローチである限り変分推論。EMアルゴリズムではない。
- EM Algorithmでは、特にのモデルはわかる(パラメタはわからない)条件で行う。
- 例えば、は混合ガウス分布だとわかっているとか。
- のモデルがわかっている以上、そこからのモデルも逆算できて、のみならず、パラメタを動かしてを変更させての最小化もできる。
- なので2つのステップで交互に最小化を行うし、変分推論よりも収束も早いし、安定もする。
一般的なアプローチは変分推論だが、特別な条件下で解きやすいのがEM Algorithmである。
変分推論
目標はをうまく推定すること。
変分推論とは、分布を推定するときに、の分布の形はわからないので、別の分布を(分布の形やパラメタを仮定する形で)考えて、それと与えられたデータをもとに得る、から得られたとのDivergenceを最小化したいものである。
には、どのような分散や平均などのパラメタ、分布の概形を与えるかについては一概に言えず、うまく選ぶのが変分推定の目標。
例えば、VAEなどではガウス分布であると固定して、与えたデータから平均や分散を計算してパラメタとして入れている。
ELBO
以下の式が成り立つ。
は計算しづらいということで、変分推論ではに置き換えている。
これはEMアルゴリズムなら、のままやっている。
式のかたちは、変分推論の分布に従ってサンプリングされたについての期待値。その中身は変な形であるが、ここではELBOが大きければ、のKL-Divergenceが小さくなり分布として一般的に近くなるということになる。
変分推論の目標は、ELBOを最大化したい。
ELBOの最大化の手順
この2つの項に分ける。前者は尤度の期待値で、これはの近似分布から計算する。
前者の計算
前者について、をで代替するとしても、のベイズの定理を用いる必要がある。
いつも通りだが、これの外に期待値をつけるので、その積分は解析的に解けない場合も多い。
解析的に解けない場合では、サンプリングによる推定をするしかない。
変分分布からサンプルを生成し、それについて、を評価(はモデルがなんなのかを定めている以上、知っている前提)。
なお、と積分する以上、実はとが共役である必要はない(logとったものとの積なので)
一般的には、ニューラルネットワークを用いたDecoderでからを復元し、その復元結果から解析的に計算できるならそれでよし、できないならモンテカルロ法やほかの数値近似方法で計算する。
しかし、もガウス分布で、もガウス分布の時、当然は共役ではない。それでも、ガウス分布の時は復元した後の平均と分散がわかれば、計算できるということ。
これは解析的に解くことができ、以下のようになる。
- は中間表現の平均
- は中間表現の分散。
- はEncoder, Decoderを通して得たものの平均。
- はEncoder, Decoderを通して得たものの平均。
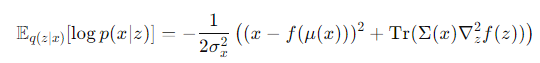
後者の計算
実をいうとよくみると、後者はKL-Divergenceそのもの。
つまり、ELBOではというKL-Divergenceの計算は求まらないので計算しなくていい代わりに、のKL-Divergenceを求める。そして、これを最小化していきたい。
どのように最大化するのか
計算の方法がわかったところで、最大化を行う。
一般的には、VAEではEncoderはであり、Decoderはである。これがガウス分布という概形で、平均分散どうのこうのは人間がそうやって仮置きして解釈しているだけである。
そして、Encoder-Decoderモデルの学習では、ELBOを目的関数にしている。
ここより下はまだわかっていない!
EM Algorithm
📄EM Algorithmの解説 を参考。
変分EM Algorithm
変分推論やEMアルゴリズム似てるよな、こいつらのコンボあるで。
