https://proceedings.neurips.cc/paper/2020/hash/98b297950041a42470269d56260243a1-Abstract.html
関連する研究
Tomoya Sakai and Nobuyuki Shimizu. Covariate shift adaptation on learning from positive and unlabeled data. In Proceedings of the 33rd AAAI Conference on Artificial Intelligence, AAAI’19, pages 4838–4845, 2019.
Introduction
既存のPUはSCAR仮定に立つものが多いが、Temporal Drift, Domain Shift, Adversarial Concept DriftではSAR仮定なので対処できない。
biased PUについての研究がある。この論文ではbiased PU learningについてさらに難しくして、恣意的にPositiveを選ぶArbitrary Positive Unlabeled Learning(aPU)を考案した。
aPUの前提条件として、どんな恣意的なBiasがあっても構わないが、すべてのNegative sampleは同じ分布に属しているという前提が必要。
aPUが使える条件設定として以下のようなものがある。
- 国境を越えた土地被覆 データセットは、国の技術標準が異なったり、ある国の財源が不十分であったりするため、存在しないことが多い[15]。だが実際に国境を越えても地形などは当然連続なので、同じ分布に従う。
- 敵対的なPU Learning 意図的に識別器を壊すようなAdversarialなselection biasを持つ。これについては、移り変わりが早く、しかも毎回意図的に識別器を壊すようなものが選ばれると考えれば、Biasがあることの最たる例である。
この論文の貢献としては以下のようなものである。
- abs PUという一般的なPU LearningのRisk推定における過学習を是正する手法を開発した。
- aPUという手法を開発した。これは通常のPUで学習した後に、UU Learningをするというものである。
- PURRという新しいaPUのRisk推定器を開発。
- 幅広い実験を行い、特にPrevious workのbiased PUを上回る結果となった。
第2章は省略
Simplifying Non-Negativity Correction
📄2017-NIPS-[nnPU] Positive-Unlabeled Learning with Non-Negative Risk Estimator で開発されたRisk推定器は以下のようなもの。
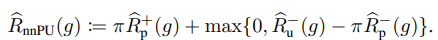
ここで、新たにABS-PUを開発。の代わりに絶対値にする。
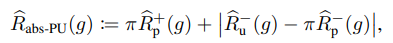
ってこれってただのGradient Ascendやないか!?nnPUもやっとったで!
ただ、nnPUはmaxの内部だけgradient asecndしたのに対して、こちらはも計算に入れている。
Arbitrary-Positive Unlabeled Learning(aPU)
問題設定として、で訓練して、へのDOmainAdaptationを考える。
また、は、つまり全部のラベルの分布を含んだの周辺分布である。
aPUの問題設定は以下の通り。Negativeサンプルの分布は常に等しい。
両方のDomainのClass Priorが存在する。
問題設定として、NegativeはおなじぶんぷでもPositiveは違う分布である。

実現したいのは以上の通り。
- 単純にtrain dataでPUを訓練する。
- 訓練したPUにreweigtingを行い、ターゲットドメインへ変換する。
aPUとCovariance Shiftについて
Covariance Shiftとは以下のようなShiftである。サンプルが違うけど、対応関係は変わらないというもの。今回の問題設定であり、baselineはbiased PUと比べる。
この時、となるので、これを推定すればいい。これの推定は、以下にあるような手法で密度比推定すればいい。
] M. Yamada, T. Suzuki, T. Kanamori, H. Hachiya, and M. Sugiyama. Relative density-ratio estimation for robust distribution comparison. Neural Computation, 25(5):1324–1370, May 2013.
全体のアルゴリズムの流れ
aPUの問題設定の変種
こっちはNegativeを固定しているが、逆にPositiveは不変でNegativeだけが変わるというのも考えられる。
ただ、PとU両方がシフトしてしまえば、追加仮定がないと学習できない。
aPUにおけるUU learningの役割
一番理想的なのは、trainデータだけで考えるときは、tr-uを完全に分類できるのが一番うれしいことである。tr-nが理想的に、もしうまくUから選び出せるのならばそれはSCARで選ばれる。
だがこれは非現実的なので、この手法ではtr-uの中のサンプルを重みづけすることで、できるだけもともとのNegativeに近い分布を選びたい。
これを実現するために、NU Learningの変形である、重みづけUU Learningをする、もう1つはSemi-supervised learningのaPNU learning。この論文はこの2つを提案した。1つ目の名前はPU2wUU, 2つ目の名前はPU2aPNUである。
アルゴリズムの流れ
aPUは2ステップのアルゴリズムである。
- からPU Learningで識別器を訓練する。
- もしBiasを考える必要があるなら、biased PUの手法で訓練する。
- そのを使って、からを選びだすように、reweigthingする。
- 選び出したNegativeを用いて、最終的な識別器を訓練する。手法はwUU, aPNUである。
ステップ1: からを近似する
これを実現するには、から学習し、の値を得たい。
まずは、でPU Learningを使う。ここでは経験損失の式の最小化なら何でもいい。
定理2
と識別器と損失関数を定義する。ラベルはである。
PN Learningについての、Negativeの項をPU Learningの訓練した識別器を用いてNegativeであるリスクを以下のように推定できる。この推定した値を、ステップ2の分類器の訓練で使用する。
PN Learningでの重み項のを割ってサイズをスケールを整える。の識別器であるとき、確実にNegativeであればあるほど、識別器による損失を加えていく感じ。
ここで、がPAC学習可能ならば、この経験リスク推定は不偏推定であり、Negativeの真の損失に収束する。
定理2で何がうれしいのか
うまいことN in Uを選び出すには、Noisy LabelのSmall Loss Trickとか、過度にPositiveに影響されないように正則化項を使う。 📄2020-Survey-A Survey of Label-noise Representation Learning: Past, Present and Future を参考。
この定理2の結果により、何かしらのという識別器が正しく訓練できていれば、それを用いてreweightingを行うことで、
ステップ2: テスト分布の分類器を訓練する
UU Learningについて、nnPUと同様にGradient Ascend込みで学習することができる。以下のように。
これを、今回の問題設定に適用させたら次の形になる。Uはtest-Uであり、Nはtrain, testどちらでも同じ分布に従っている。UU Learningの形らしい。は選ばれたNegativeであり、もともとはからきているのでUUってことかな?
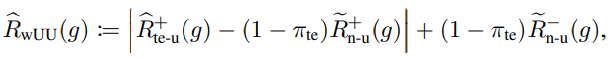
Pデータの再利用によるRisk推定
分布として、が重なっている場合、は理論上有効に使えばTarget Domain Pに対しての情報を持つことができる。こういう時に、Semi-supervised Learningを用いることでよりよい手法を考えることができる。
📄2017-ICML-[PNU]Semi-Supervised Classification Based on Classification from Positive and Unlabeled Data では、Semi-supervised Learningベーすの手法を考えた。この中で、PNU Learningというフレームワークを考えた。のハイパーパラメタ。
これをもとに、aPNUの式は以下のようになる。
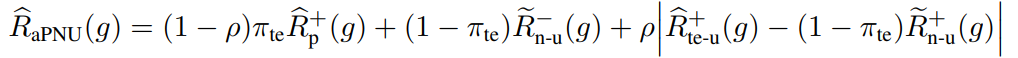
- の時はaPNUはテスト分布とTrainのUから選んだNだけを見て、PN Learningする。
- ならばwUUと同じ、NU Learningになる。
Positiveの間に大きいCovariance Shiftが存在する場合、2つのドメイン間の知識を運搬することが難しく、PN Learningしたほうがいいらしい。なのでは1に近くなる。
Positive-Unlabeled Recursive Risk Estimation
先にを推定してから本命のを推定するのは最初間違えると、後に響きすぎて辛い。
これらを連結した(同時にやるってことかな?)ままやるってできるのかな?できます。
Uについての期待値をPとNの式に分解するということはできる。この時、PかNの片方がわかっていればそれでPU、NU Learningできる。では、両方がわからないときには、再帰的に代入みたいにできそうだよね?
Positive-Unlabeled Recursive Risk
上のようにPN Learning1のように定義ができるが、これについては解けないので、の書き換えを行う。なぜなら、Negativeは常に同じ分布であるという問題設定だから、trainのデータから転用できる。
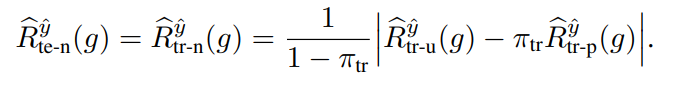
次に、について、これをNUで分解すると、以下のようになる。
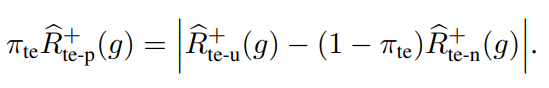
これらを踏まえて代表すると、以下のようになる。

よく考えるとこのように展開することもできるよね。正直何がいいのかわからない(複雑な式ほどまずくね?)
Experiment
つまりaPUでは、aPNU, wUU, PURRの3つの手法を提案している。実験を走らせてみた。
baisedがないときはnnPUのほうがよかった。
biasが入るとbias考慮しないものは性能下がるけど、これはよいまま。
