Sen(Qian)’s Memo

同時に複数のタスクを学習することで、1つのタスクに偏った特徴抽出器にしづらくすることができる。=Multi Task Learning。

Multi Task Learningがうまく行かない=更新するべきGradientの向きが真逆で、合計したGradientを更新していきたいけど、ほぼ真逆ならGradientが0になりがちで、鞍点での学習が遅いが起きる問題が(鞍点ではなくても起きてしまう)。📄NNDL 第7章 Networkの最適化と正則化 の手法を参考。

先行研究では、タスクごとのgradientの重みの寄与を調整したりとかしていた。この研究では、Gradientが衝突することが問題であるので、1つのベクトルと直交となるベクトルが作る超平面に射影して評価するらしい。

曲率半径が小さい=めちゃくちゃまがっている。

ガウス曲率は以下の記事を参照。

各タスクごとのgradientを$\mathbf{g}_i$とする。

GradientがConflictしている=開いてる角度が90度以上=cosが負。

また、以下の条件を満たすと、Multi-Task Learningで性能が下がる。

1. Gradient Conflictが起きる。
2. Gradientごとの大きさが大きく違う。
   1. 指標として、以下のようなものを導入する。0から1を取り、同じ大きさ程、高い値を取る。

   

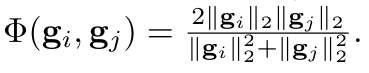
3. ガウス曲率が大きい。

この論文では、この3つをGradientを変化させることによって解決させようというもの。

為す角度のcosが負であれば、あるベクトルに直交するベクトルの集合=超平面上に写像する。(以下の式になる)。

この操作について、以下のようにするのがアルゴリズムである。

1. あるタスクについてのGradient$\mathbf{g}_i$を選ぶ。
2. 次に、それ以外のタスクのGradient$\mathbf{g}_j$について全部イテレーションする。
3. $\mathbf{g}_i, \mathbf{g}_j$のcosine類似度が負であるとき、上の$\mathbf{g}_i$の更新の式で更新する。
   1. つまり、$\mathbf{g}_i$と直交するような超平面の上に写像したものを更新していく。

このようにGradientをがちゃがちゃ弄っても、ちゃんと凸関数ならばこの手法で最適解に収束すると示せる。