2017-MLJ-Class-prior Estimation for Learning from Positive and Unlabeled Data

Journal Paperなので非常に長い。

Introduction

PositiveとUnlabeledは以下の通り。

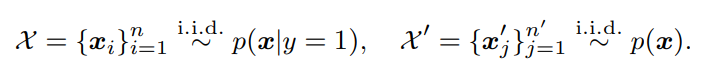
そして、実際には知らないが、Negativeのデータの分布というものがあり、全体の分布はClass Prior $\pi$ というPositiveのものの割合を使って、以下の混合分布のようになる。

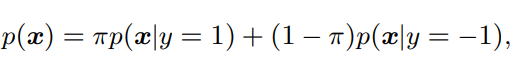
この論文では、Positiveのデータセット $\mathcal{X}$ とUnlabeledのデータセット $\mathcal{X}^\prime$ のみを使って、Class Priorの $\pi$ を推定するのが目標。

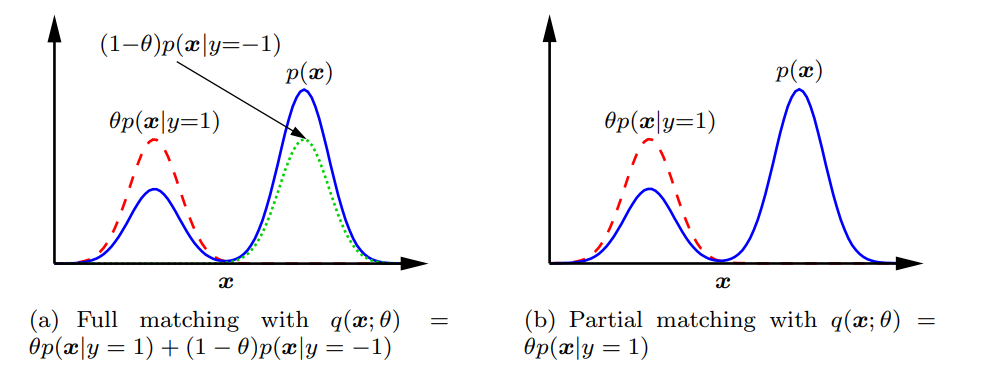
前提として、Positiveの密度分布関数 $p(x|y=+1)$ とNegativeの密度分布関数 $p(x|y=-1)$ がわかっていれば、図(a)のように理論上峰の高さから、Class Priorを計算することはできる。その距離は一般的にはKLダイバージェンスやf-ダイバージェンスを用いる。

一方、図(b)のように、片方しかわからない場合は、最高峰の比較ができないので、推定が難しい。(Positiveデータしかないので計算自体はできるが、正規化とかいろいろ丁寧にやらないと…)

こういう前提に立って、KLダイバージェンス、Pearsonダイバージェンス、L2距離による最小化、MMDが先行研究としてあった。しかし、PositiveやNegative両方のクラスからのLabeled Samplesが必要である。

ここで、図(b)のPartial Matchingの提案は2014に提案されている。以下のDivergenceを最小化させる。( $\theta$ がClass Priorである)

q(\mathbf{x}; \theta) = \theta p(\mathbf{x} | y=+1) \\ \theta = \argmin_\theta Div_f(\theta)

しかし、この論文では既存のすべての手法はClass Priorを過大評価していたことを示す。そして、f-divergenceに適切なペナルティを科すことで、正しく推定できることも示す。L1距離によるペナルティから着想を得ていそう。

提案手法

先行研究はなぜ過大評価してしまうのか

f-divergenceにおいて、 $t\geq1$ で最小値を持つ $f(t)$ を考える。そして微分可能であり、 $t<1$ の時は $\partial f(t) < 0$ で、 $t=0$ の時だけ $\partial f(t)=0$ となる。この条件はPearson, KL Divergenceのいずれも満たす。

次に、f-divergenceの計算をする式を、 $t$ で微分することで極小値をとる点を求めていく。つまり、以下の式が0となる。

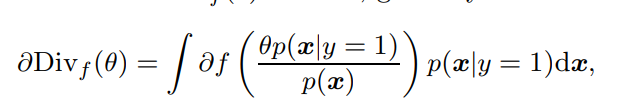
しかし、仮定により以下のような条件付確率と書くことができるので、 $f$ に入れる値は $[0,1]$ であり、先ほどの仮定により微分は負かゼロとなる。

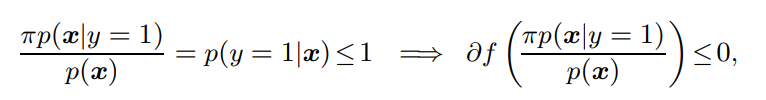
このことを踏まえて、 $\partial Div_f(\theta)$ を計算する。積分を計算するとき、 $Pr(y=1|\mathbf{x})=1$ の領域 $D_1$ と、 $Or(y=1|\mathbf{x})<1$ の領域 $D_2$ に分けて積分する。

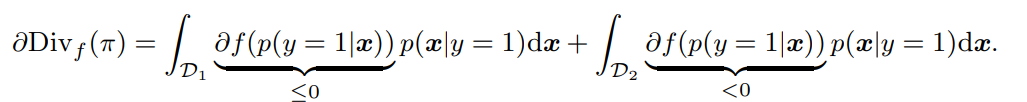
これの極小値を求める、つまりこの式が0をとるときは、 $p(\mathbf{x}|y=+1)=0$ の時だけ。これは非現実的な仮定。それ以外の時は、明らかに上の導関数は負の値をとる。よって、Divergenceの最適化をするなら $t>1$ で値をとることになるが、確率の性質上これは正しくないので、 $\theta$ は過大評価されている。

f-divergenceによるペナルティがあるPartial Distribution Matching(提案手法)

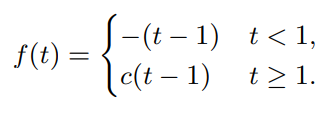
f-divergenceの関数 $f$ を次のように改造する。 $c$ は定数であり、 $c=1$ の時はただのL1-Divergenceである。このように調整を施すことで、 $\theta = \pi$ となり、ただ最適化すればいいだけというのが目標である。

まず、 $p(y=1|\mathbf{x})=1$ が $D_1$ では成り立つので、以下のように書き直せる。

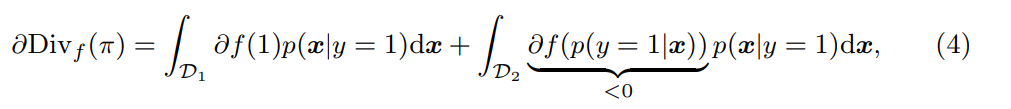
$f(t)$ は基本 $t=1$ で微分不可能であるので、劣微分を考える。

劣微分とは、微分不可能な点において、接線を引くときにとれる傾きの閉区間を微分係数として扱うというもの。基本的に凸関数にのみ使われる概念。

計算すると、劣微分 $\partial f(1) = [-1, c]$ である。よって、劣微分によって、 $t=1$ における微分係数は以下の区間となる。

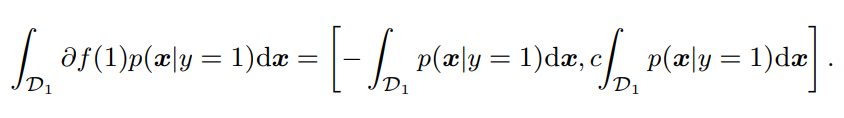
そして、 $D_2$ の区間で定めた $f$ は $t < 1, \partial f(t) = -1$ となるので、以下のように書き換えられる。

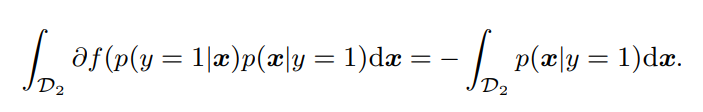
ここで、f-divergenceで導関数が0となるには、 $\partial Div_f(\pi)$ があらわす区間の中に0が含まれる必要がある。つまり以下の条件。

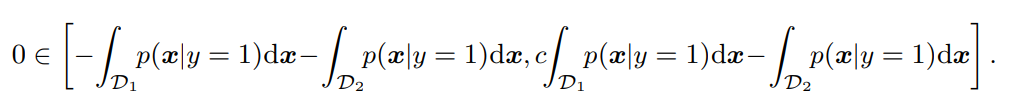
この区間の右辺が0未満だと持たないということになる。

ここで解決法として、 $c \to \infty$ と提案している。

これでは単純に $f$ は等倍としているだけである簡単な写像である。もちろん、本来の関数 $f$ を使ったf-divergence荷重適用できる。以下のようにすればいい。

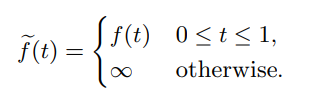
このように、提案した $\tilde{f}(t)$ によって、Class Prior $\pi$ の過大評価を防げるというもの。

ペナルティつきf-divergenceの直接な評価

Fenchelの双対性定理について解説(GPT先生)

凸関数と凸集合

凸関数: 関数 $f : \mathbb{R}^n \to \mathbb{R}$ が凸関数であるとは、任意の $x, y \in \mathbb{R}^n と \lambda \in [0, 1]$ に対して次の不等式を満たすことを言います

f(\lambda x + (1 - \lambda) y) \leq \lambda f(x) + (1 - \lambda) f(y)

凸集合: 集合 $C \subseteq \mathbb{R}^n$ が凸集合であるとは、任意の $x, y \in C と \lambda \in [0, 1]$ に対して、点 $\lambda x + (1 - \lambda) y$ が $C$ に属することを言います。

凸共役（Legendre-Fenchel変換）

関数 $f$ の凸共役 $f^*$ は次のように定義されます：
ここで、 $\langle y, x \rangle$ は $y$ と $x$ の内積を表します。

f^*(y) = \sup_{x \in \mathbb{R}^n} \{ \langle y, x \rangle - f(x) \}

Fenchelの双対性定理

Fenchelの双対性定理は、以下の最適化問題の対について述べています。

主問題（Primal Problem）

\min_{x \in \mathbb{R}^n} \{ f(x) + g(Ax) \}

双対問題（Dual Problem）

\max_{y \in \mathbb{R}^m} \{ -f^*(A^T y) - g^*(-y) \}

ここで、 $f$ と $g$ はそれぞれ $\mathbb{R}^n$ と $\mathbb{R}^m$ 上の凸関数、 $A$ は $\mathbb{R}^m$ から $\mathbb{R}^n$ への線形写像（行列）、そして $f^*$ と $g^*$ はそれぞれ $f$ と $g$ の凸共役です。

定理の内容

Fenchelの双対性定理は次のように述べられます：

弱双対性: 任意の $x \in \mathbb{R}^n$ と $y \in \mathbb{R}^m$ に対して、

f(x) + g(Ax) \geq -f^*(A^T y) - g^*(-y)

強双対性: もし $f$ と $g$ が下半連続な凸関数であり、さらにある点 $\bar{x} \in \text{dom}(f)$ と $\bar{y} \in \text{dom}(g)$ が存在して、以下の条件を満たすなら、
$f(\bar{x}) + g(A\bar{x}) = -f^*(A^T \bar{y}) - g^*(-\bar{y})$

これを強双対性と呼びます。すなわち、主問題の最適解と双対問題の最適解が一致するということです。

ここでは、スカラーであるので凸共役は単純な積である。つまり、凸共役は $f^*(y) = \sup_{x} \{ xy - f(x) \}$ である。右辺はsupなので、不等式として以下のように書き換えられる。

f(t) \geq tz - f^*(z)

そしてここに以下のように代入する。 $t$ は $r(\mathbf{x})$ という新たな関数で書けるとする。

z = \frac{\theta p(\mathbf{x} | y = 1)}{p(\mathbf{x})}, t = r(\mathbf{x})

代入したのち、両辺に $p(\mathbf{x})$ を乗じてから、積分をすると左辺はf-divergenceとなる。右辺について、同様に積分するだけではなく、任意の $r(\mathbf{x})$ について成り立つので、最大のものを選ぼう、ということ。

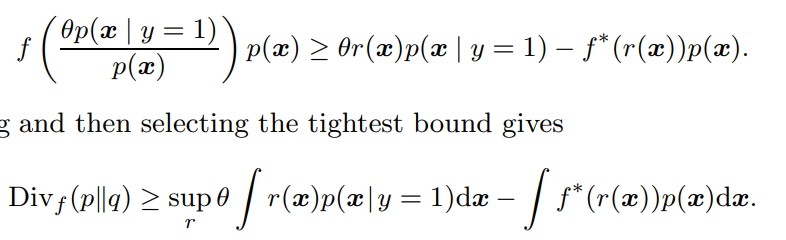
この式について、もし $r(\mathbf{x})$ は線形関数である場合、経験的な式に直す(確率との積分が総和になる)と、最適化はやさしい。なぜならば、右辺は $r(\mathbf{x})$ も線形関数で凸関数、 $f^*$ も凸関数であるので、凸最適化しやすいから。

ペナルティ付きL1距離推測

色々書いてあるが、相対で考えると凸最適化できるいい性質を持っている！を力説している。

Theoretical Analysis

省略します…