Sen(Qian)’s Memo

元論文のリンク

2020年のサーベイ論文。弱教師学習本よりも、とりわけPUについてまとめている。

PU Learningの現実での応用例

1. パーソナライズされた広告のクリック。押されなかったからと言って興味がないわけではない。
2. 診断されてないからといって、必ずそれにかかっていないことはない。
3. 知識ベースという知識のタプルがある。学習してないタプルだからと言って、その組み合わせは嘘であると言えない。

PU Learningの鍵となるResearch Question

1. PUのデータから学習するという問題にどう帰着するか。
2. 学習アルゴリズムを容易に設計するときには、どのような仮定が必要か。
3. PUのデータからクラス事前確率$p(y = +1)$を推定できるか？それは有用か？
4. PUのデータからどうして上手くモデルを学習できるか。
5. モデルの性能をどう評価すればいいか。
6. 実世界ではどのような応用があるか。
7. 他の機械学習分野へどう影響するか。

一番理想的なケースである。$\mathbf{x}$ の周辺確率分布は以下のように得られる。 $\pi = p(y = +1)$。

Positive Unlabeledによる二値分類

一般的には、PUデータは $(\mathbf{x}, y, s)$とラベル $s$を拡張。1ならばラベル付きである。ラベルが付いてるものは全てPositiveであるという仮定なので、 $p(y = +1 | s = +1) = 1$。

Positiveのデータは $\mathbf{x} \sim p(\mathbf{x} | y = +1)$から得られる。各Positiveのデータについて、選ばれる確率 $p(s = +1 | \mathbf{x}, y = +1)$はPropensity Scoreと呼んでる論文もある(2019 Bekker)。2008 Elkan, Notoにも指摘しているように、(後述する) $p(s = +1)$がわかる、single-training-setの場合は、一様にPositiveのなかから選ぶのであれば $\mathbf{x}$に依らない定数倍が成立する。

Elkan, Notoらの論文での説明をそのまま持ってきた。

基本的には、いずれのデータセットも分布からデータを得るときはi.i.d.である。

基本的には、ランダムに訓練データは $p(\mathbf{x}, y, s)$の分布から選ばれる(もちろん $p(s = 1 | y = 0) = 0$というのが成り立つ分布)が、 $y$の情報を落としてデータとしては $(\mathbf{x}, s)$のみを得る。

今回の場合はsingle-training-setシナリオというものであり、以下の手順で行う。

1. $p(\mathbf{x}, y, s)$の分布から1回、一定数サンプリングしてこれを $D$とする。
2. $D$の中で $s = 1$となる部分をPositiveとする。
3. $D$の中で $s = 0$となった、つまり残りのすべてをUnlabeledとして扱う。

このサンプリング方法では、一度だけのサンプリングして、そこから $p(s = 1)$は計算できる。具体的な組成の分布は以下の通り。 $e(\mathbf{x})=p(s=+1|\mathbf{x})$の傾向スコアを使えば、 $\alpha=p(y=+1)$を、rewriteして $2\alpha$の係数がある項など出さずに、以下のようにすることができる。

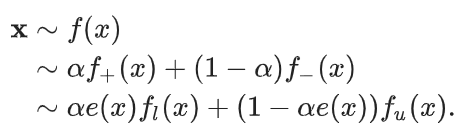
一方、case-controlシナリオでは、以下の手順で行う。

1. $p(\mathbf{x}, y, s)$の分布から1回、一定数サンプリングしてこれを $D _1$とする。
2. $D _1$の中で $s = 1$となる部分をPositiveとする。
3. $D _1$の $s = 0$の部分、すなわち残ったすべてを捨てる。
4. $p(\mathbf{x}, y, s)$の分布からもう1回、一定数サンプリング(さきほどと同数である必要もない)して、これを $D _2$とする。
5. $D _2$の全てをUnlabeledとする。(つまり、single-training-setのように $D _1$の $s = 0$なら全部ここに入るわけではない！)

こちらの方が一般的である。ただし、欠点としては2回のサンプリングの母数は同数ではないし、1回目のサンプリングの母数がいくつなのかもわからないことが通例なので、 $p(s = 1)$の推定はそもそもできない。下図のようになる。

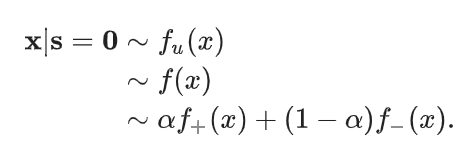
この論文では後者を論じる。大は小を兼ねる！

2008 Elkan, Notoらの論文を見ると詳しく解説されている。

Unlabeledには、本来Negativeと本来Positiveだがラベル付けされなかったものの2つが混入している。故に、ラベル付けのポリシーとクラスの分布を仮定しなければならない。

一様にランダムに選ぶ！これが一番前提として使われている。これはcase-controlシナリオに多く、分布からi.i.d.で選ばれている。
このようにラベル付けすると、通常の二値分類の手法をほぼそのまま転用できるという利点がある。

定式化すると、ground truthがPositiveつまり $y=+1$であるならば、 $\mathbf{x}$に関わらず、選ばれる確率は一定の値を取るということ。

これに基づく重要な性質として以下のようなものがある。

1. $p(y = 1 | \mathbf{x} _1) > p(y = 1 | \mathbf{x} _2) \Leftrightarrow p(s = 1 | \mathbf{x} _1) > p(s = 1 | \mathbf{x} _2)$　順序は常に保たれる。
   1. ラベルが付く確率は一様であるが、そもそもPositiveでなければラベルが付かないということを考慮してこういう形ってことかな？
2. 定数倍なので、 $p(s = 1 | \mathbf{x})$を訓練すれば、 $p(y = +1 | \mathbf{x})$が得られるようになる。

これの発想は、欠損データは一様にランダムに発生するという仮定から着想されたらしい。

データ $\mathbf{x}$の性質によって、ラベル付けられる確率が変動する、というものである。 $p(s = 1 | \mathbf{x}, y = +1)$がそれぞれ異なる感じ。

SARの1つの典型例として、Negative例に近いPositive例ほど、選ばれにくくなると仮定する。ラベル付けのされやすさとしては、以下の式で考えられる。

ラベルが付く確率は、狭義単調増加の関数 $f$が存在するとして、以下の式から各点のラベル付けされる重みが算出されるとする。

そのうえで、ラベル付けされたかどうかで判断する観測されるProbabilistic Gapとして、以下のものだと定義する？。WHY?

重要な性質として以下の2つがある。

1. $\triangle \tilde{p}(\mathbf{x}) \leq \tilde{p}(\mathbf{x})$実際に観測するgapは真のgapより小さい。
2. $\triangle \tilde{p}(\mathbf{x} _1) = \triangle \tilde{p}(\mathbf{x} _2) \Leftrightarrow \triangle p(\mathbf{x} _1) = \triangle p(\mathbf{x} _2) \\\\ \triangle \tilde{p}(\mathbf{x} _1) \leq \triangle \tilde{p}(\mathbf{x} _2) \Leftrightarrow \triangle p(\mathbf{x} _1) \leq \triangle p(\mathbf{x} _2)$　順序性が同様に成り立つ。

これは2018 Katoらの論文で使われた鍵アイディア。彼らは以下の仮定を使った。

さきほどのSCARと違うのは、あれは $y = +1, y = -1$のみで成立していた？のだが、これは同じ $y = +1$のデータの間でもこれが成り立つということだろう。

基本はすべてのNegativeと一部のPositiveがUnlabeledであり、残ったPositievだけラベル付けされていること。そして、2つのクラスは分離可能であり、分布の確率分布はなめらかな確率密度関数を持つというもの。

Unlabeledを全部Negativeとして扱うという非常に乱暴なテクがある。もうこれはさすがに語る余地もないだろ。それはそう。

2つのクラスを完璧に分離可能にする分類器が存在するという仮定。この仮定に基づけば、ラベル付けされた例のすべてをできるだけPositiveとして分類することを優先するという方法になる。後述の2-stepsテクニックに活用されるらしい。

お互いに近いデータ点は、同じような $y$を持つ(Positive or Negative)。数式で書くと、 $\mathbf{x} _1, \mathbf{x} _2$が近いのであれば、 $p(y = +1 | \mathbf{x} _1), p(y = +1 | \mathbf{x} _2)$は近い値を取る。

つまり、すべての$s = 1$のデータ点から遠い点こそが信頼できるNegativeの点だと考えられる(ほんとうにNegativeである保証はない)。これも2-stepsテクニックで使われるらしい。これは距離別で教師なし？的な手法を使う時でよく見られるかもしれない。

SCARにおける重要な役割を果たす。仮定で強い順から並べる。

1. 完全分離可能な分布たち　完全分離できるのならば、未ラベルのうちのPositive例と分布が理論上一致できる。
2. 完全に分離できる一部のドメインを持つ　データ $\mathbf{x}$の成分の一部では完全にPositiveだけを含むことができる、という例。のうちの一部が完全に $y = +1$であるとわかれば、そこにおいての $s = 1$の割合から、ラベルが付く頻度がわかる。(これは書いてないがこういうこと？　ラベルの付く頻度から逆算して、クラス事前確率がわかる)
3. Positive関数の仮定　成分の一部をそのままではできないが、上手く変換する関数があるとして(カーネル法のように？)、変換した先では完全に分離可能な分布。
4. 非還元可能性　Negativeの分布がPositiveの分布を完全に含むことはない。もし、これが成り立つなら、Positiveを特定したとしてもNegativeのなかにPositiveがあることになり、そもそもの仮定が破綻。

これはJessarらの論文でもあった。

一般的に使われるのは、F1スコア。

$p=p(y=1|\hat{y}=1), r=p(\hat{y}=1|y=1)$としたとき、これの調和平均がF1スコア。

SCAR仮定では、 $r=p(\hat{y}=1|y=1)=p(\hat{y}=1|s=1)$が成り立つが、Precisionは計算できない。そこで、代替策として以下の指標が2023 Lee, Liuによって提案された。

G検定という相互情報に基づく独立性検定がある。これは特徴選択、構造学習に使えるらしいが、PNと同様にPUでもできるらしい。ただし、データの性質？で補正係数で補正しないといけない。特徴選択をするときに、なんかUnlabeledをNegativeとみなしても変わらないらしい。

SCAR仮定という強い仮定の下では、ラベル付け確率 $p(s=+1)$ OR クラス事前確率 $p(y=+1)$を推定できれば、Unlabeledの中でのPositiveの割合の期待値がわかる。また、観測されたPositieとUnlabeledにあるground-truthのPositiveの順位分布？は同じではなければならない。

これらがわかれば、全体におけるground-truthがPositiveである割合、個数がわかるので、F1スコアとかが計算できるらしい。

結論として、 $p(s=+1), p(y=+1)$のうちのどれかはPU Learningで知らなければできないのは？ということ。

三種類に大別できる。

キレイに分割できるSeparability, 近い点は大体同じ結果を出すSmoothnessが必要。

1. 信頼できるNegative例をUnlabeledの中から探し出す。
   1. とにかくPositive例から遠いのがNegativeであるという考えがあるので、上手く距離関数の定義をしてやったりできる。2000年代の主流。
2. (自己)教師あり学習を用いて、Positiveと選んだNegative、使いたいなら残ったUnlabeledを使って訓練する。

これがResamplingなどとよく言われる。

ステップ2=(自己)教師あり学習を使って、step1で選んだpositiveとnegative、場合によってはunlabeledを元に学習する。

Step3として、EMアルゴリズムのような片方を固定しての最適化をするとき、何をもってして終了条件とするのかと考えることができる。

Biased PUはUnlabeledをNegativeだがラベルNoiseがある者として扱う。SCARの条件下だと仮定する。Noiseに関しては、明確に $s=+1$の例をNegativeに分類してしまったときのペナルティをかなり大きくする感じ。

重みをつけたbiased SVMというのがよくある話。そして、イテレーションごとにbiased SVMを行い、信頼できる例の誤分類に大きなペナルティを与えるというやり方もある。また、各Unlabeledの例について、与えられた $s=+1$の例から最も近い点との距離をもってして、各点の誤分類のペナルティを設定するやり方もある。(遠いほど小さい)

ただ、Negativeとみなした中にある大量のPositiveによるNoiseは学習を難しくしている。これについて、Baggingや最小二乗SVMで対策できる。

Baggingとは、Bootstrap(重複許容してサブセットを選ぶ)して、各サブセットについてそれぞれ訓練させてその結果をアンサンブルさせる。Positive例もresamplingすることでよりロバストになるらしい。

その上で、Biased least Squares SVMは局所学習という、近い距離の点は同じラベルを取るような正則化項をつけたのもある。その際距離としては、ユークリッド距離ではなく、下式のMahalanobis距離を使うとより良いらしい。 $\mu$は平均ベクトルで、 $\Sigma$は共分散行列。

RankSVMはマージンベースのpairwise lossを最小化させるSVMである。クラスごとにペナルティがないが、お互いのペア間でペナルティを付けていく感じ。他にも手法はある。

重み付きロジスティック回帰では、正しくPositiveを分類することを正しく $y=-1$を分類することより重みを重くする。Positiveには $p(s=0)$、Unlabeledには $p(s=+1)$とラベル付けを行う感じ。ラベルが付いてる方が少数派なので、おのずと重みが出る。この手法では従来の分離手法で行っているので、当然分離不可能なクラスでは完全な分離は原理上できなくなる。

Positive例の間は絶対にリンクする制約、違うクラス間には絶対にリンクはしてはいけないという重み付き制約ありクラスタリングを行う。(これもpairwise感ある)。Positiveが少ないときに役に立つ。

01から作る行列を、行列欠損値補完と考えられる。

うーん、よくわからん！

具体的には、以下の3つがある。

• postprocessingは非伝統的な分類器(なんだよ)で、UnlabeledをNegativeとして扱ったまま訓練したうえで、出力する確率をcalibrateする感じ
• preprocessingはclass priorで訓練するデータセットを変更する感じ。みんなだいすきcost-sensitiveな手法たちは皆確率であらかじめ乗じて重みを変えている。
• method modificationは謎。

📄2008-KDD-Learning Classifiers from Only Positive and Unlabeled Data によれば、SCARの条件下では、 $p(s=+1|\mathbf{x})=c p(y=+1|\mathbf{x})$が成り立つ。この論文の中で提案された手法としては、まず $p(s=+1|\mathbf{x})$を訓練して、それに定数倍乗じれば $p(y=+1|\mathbf{x})$というもの。

一般的にはPositiveかどうかは $p(y=+1|\mathbf{x})>0.5$で判断するが、これが変わることもある。0.5を境目にすると考えるとならば、以下のように符号で判断もできる。

まあ正直postprocessingはこれぐらいの存在感では…?

訓練するデータセットに手を加えて、通常のPositive Negative Learningで学習できるようにする方式。

以下の3パターンがある。

Rebalancing Method

PUで学習させた非伝統的な分類器がPNで訓練した伝統的な分類器とできるだけ同じ性能を維持できるように、各サンプルに妥当な重みを付けること。

$\mathrm{positive:}\:\: w^+=1- c\tau \\ \mathrm{unlabeled: }\:\: w^-=c\tau$

通常は0.5の前後で分類するので、 $\tau=0.5$と代入すればすっきりする。

reweightedしたあとにロジスティック回帰したりすることができるらしい。

他にも、rank pruningというnoiseに強い手法もある。データの中から選択的に削除して、信頼できるPositiveとNeativeの身を残して学習するという形。それらについての重みは $p(y=+1)$としてそれを満たすように割合を決めればいい。

この手法は、分類器の判断する閾値 $\tau$に興味あるが、 $p(y=+1|\mathbf{x})$に興味がないときに使う。

ようわからん。論文みるべき。

https://eva.fing.edu.uy/pluginfile.php/63457/mod_resource/content/1/Elkan_2001_The_foundations_of_cost-sensitive_learning.pdf

ラベルの確率を組み合わせる。

📄2008-KDD-Learning Classifiers from Only Positive and Unlabeled Data にある手法で、Unlabeledの各サンプルについて、 $p(s=+1|\mathbf{x})$がある前提で(さらにUnlabeledについての精度を上げるためにもう1回計算する)以下の式でreweightingする。 $w$がPositiveであり、 $1-w$がNegativeである感じ。

$w(\mathbf{x})=p(y=+1|s=0,\mathbf{x})=\frac{1-c}{c} \frac{p(s=+1|\mathbf{x})}{1-p(s=+1|\mathbf{x})}$

経験損失最小化

損失関数を用いて、以下の経験損失を最小化するように $g$を訓練すること。

$R(g)=p(y=+1) \mathbb{E}_{p} [l(g(\mathbf{x}), +1)] + (1-p(y=+1)) \mathbb{E}_{n} [l(g(\mathbf{x}), -1)]$

ただし、この損失関数はPN分類に使われるもので、PUにするにはrewriteが必要。rewriteの結果は 🚫 Post not found にある。

よく使われる損失は以下の通り

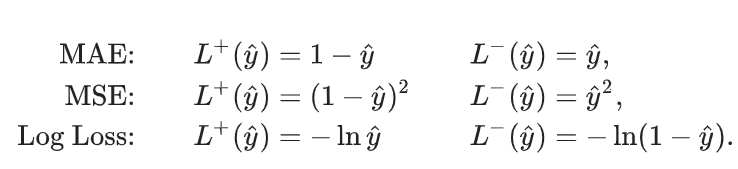
上はSCAR仮定の下での式である。だが、傾向スコア(Propensity Score) $p(s=+1|\mathbf{x})$が定数ではないときには、reweite前では以下のようになる。具体的にはこちらを参照。

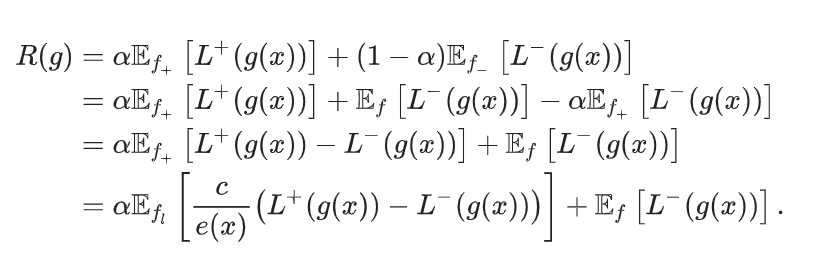
このように、case-controlはrewriteしなければ直接学習に使うことができない。

一方で、single-training-setでは、前述の仮定によって、 $2 \alpha$の係数が出てくるようなrewriteしなくても、書き換えられる。

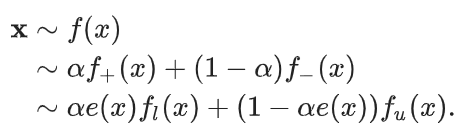
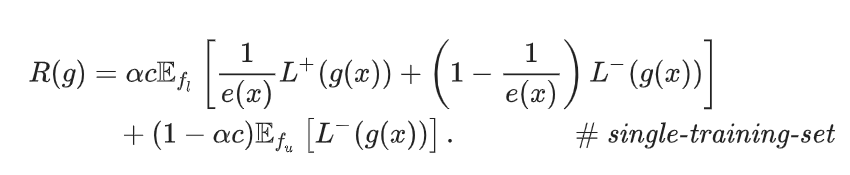
このかたちは、Bekkerらが [[ここに論文]]で指摘した、propensity scoreによる重み付けにあたるとした部分。

前述の行列補完のShiftMCという手法はSCARにおけるこれの特殊ケースらしい。

Positive、Negativeのデータをカウントして、それをもとに各種の重みなどのパラメタを決定する。

POS4.5というアルゴリズムがある。 $L_i, T_i$はノード $i$における $s=+1$の数と該当ノードのサンプルの総数とする。ノード $i$での正例数の予測は $\hat{P}_i = \min(L_i / c, T_i)$、 $\hat{N}_i = T_i - \hat{P} _i$である。

このような予測は割としっくりくる。

ほかにもベイズでの分類器などがある。

新しい関係を探して、それを関係性データベースに加えることで、自動的に作り上げる。

実はこのプロセスは、知識ベースにあるものをPositiveとして、追加可能なありうるデータのすべてをUnlabeledにすることができる。ほんとどんは知識ベースにないものをNegativeとして扱っているんだけどね。そういう考え方もある。そもそも関係性では、分離可能性を仮定しているので、相性がいいことにはよい。

関係データでSCAR仮定が成り立つなら、古典的なクラス事前確率の組み込みの関係版を適用することができる。

まだあるがここは理解できなかった。

GANをPUに導入した研究もある。

同時訓練は自己教師あり学習であり、同じデータに対しての2つの視点で同時に2つのモデルを学習する。これにPUを適用させたものもある。

データ流分類という、連続したデータの分類に含まれるパターン安堵を検出するというもの。これについての研究もそれなりにある。

Bekker 2019で、EMアルゴリズムを用いた、SAR仮定下での学習が提案されている。

• データが明らかに分離可能性が高いならば、2 step法。SCAR仮定が使えるのならば、リスク最小化。
• どちらも兼ね備えている場合、いくら分離可能だとしてもお互い近くにデータがあるならばSCARのほうがより良い。
• 明確な分離があるとき、極端なSAR仮定においてもロバストであるとわかる。
• Positive and Generalized PUは2stepであり、2stepの中でも頭1つ抜け出している。
• クラス事前確率を使うcost-sensitiveな手法は、SCAR仮定が破壊されてSARになったらまずい。

非伝統的な分類器は $p(s=+1|\mathbf{x})$を訓練して、そこから $p(s=+1|y=+1)$を用いて、 $p(y=+1|\mathbf{x})$を逆算する手法である。

逆に伝統的な分類器とは、いきなり $p(y=+1|\mathbf{x})$を訓練する。

Northcutt 2017が提案したRank Pruningという手法では、まず非伝統的な分類器 $g$を訓練する。そして、 $s=+1$全体の中に占める $g$によってもラベル付きと判断される割合を超えるサンプル、つまり $g(\mathbf{x}) \geq p(\hat{s} = +1| s = +1)$であるのを、Confidently Positive Sampleという。 $\hat{s}$は $g$による予測結果を0か1にしたもの。ここで、Confidently Positive Sampleは $s=+1$であるとは限らない。

そして、 $g$によって $\hat{s}=+1, s=0$となっているものは、ラベルがついてないけど自信満々なPositiveだとみなせる。よって、 $p(\mathbf{x}|\hat{s} = +1)=p(\mathbf{x}|y=+1)$として疑似的に全部Positiveとみなした時、 $p(s=+1|\hat{s}=+1)$はラベルがついてる確率。と推定できるという算段である。

もう1つの手法としては、 $p(s=+1|\mathbf{x})=c p(y=+1|\mathbf{x})$の左辺を学習できるわけだが、もし $p(y=+1|\mathbf{x})=1$つまり確実に $y=+1$になると仮定すれば、左辺は $c$となる。

このことを利用して、何かしらの $\mathbf{x}$で $p(y=+1|\mathbf{x})=1$が成り立つとする。この時、まさに $\max g(\mathbf{x})$をとれば、それが確実にPositiveだとして、 $c=\max g(\mathbf{x})$が成り立つこととなる。

下図のように、できるだけ2つの分布の重なりを減らしたい！という考えから出発する。

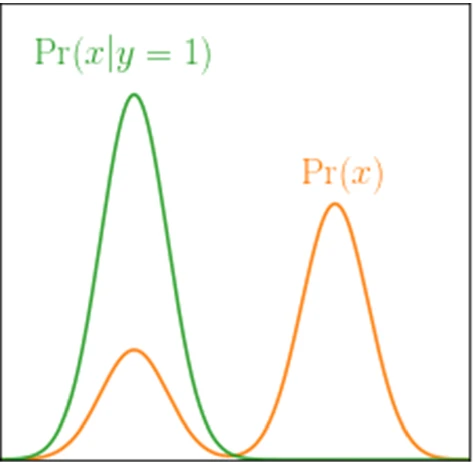
ただし、このままでは、下図のように、PositiveとNegativeの境目の確率密度が非0つまり、分離不能の時に、赤みたいな過学習が起きてしまう。それを防ぐために、超えた分はペナルティ項として与えて、できるだけ黄色以下に押さえつけたいという感じだ。

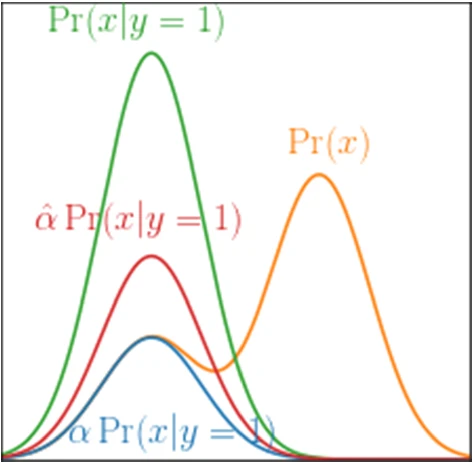
決定木でラベル付け頻度の下界を探るらしい。よくわからなかった…論文の本体を読もうと思う。

$p(\hat{y}=+1|y=0)$を最小化したいので、 $p(\hat{y}=+1|y=+1)$を最大化をしていく。

後者はPUデータから計算できる。(どうやって？ $p(\hat{s}=+1|s=+1)$で代用？)

よくわからなかった…後で本体読みたい。

あるカーネルを用いて、全体の分布 $p(\mathbf{x})$からうまく $p(\mathbf{x}|y=+1)$を分離できれば、という手法もある。

分離が完全にできるのならば、一番楽。Elkanらの論文の手法が一番。ただ現実では分離ができないのが普通なので、partial mattchingを使うことになるだろう。

あとはいろいろ書いてあったけど前の部分が理解できてないので理解できません…

病院に行く患者がいい例。病院に行ってNegativeと言われたのだとしても、そもそも病院に行かない人は評価できない。

また、推薦システムがあるサイトでの購入のように、購入された＝Positiveにすると、明らかに推薦されたというバイアスが存在する。

また、大学の授業に出る人はActiveでも、でない人がActiveではないと一概に言えない。

Case-ControlシナリオとSingle-Training-Setシナリオはいずれも現実に即しており、Case-Controlが完全にSingle-Training-Setを包含しているといえる。

negativeの分布がかわるがpositiveが変わらない場合=Negative-class dataset shiftも考えられる。これはAdversarial Trainingがいい例。

社会的な圧力などがあって思ってないことでも世間体のためにうそのことをいうことがある。これもバイアスつきのPUと考えられる。

外れ値検出のような、1クラス分類もPUのシチュエーションではできる。全体のデータがUnlabeledであり、一部のPositive例だけが与えられているみたいな。

自動的な知識ベースの補完もPUだと考えられる。前述の書かれていない知識は必ずNegativeとは限らない、というものである。

原因を特定する問題でも、(どの遺伝子が決定的な効果をもたらしているか)PUとみなせるらしい。(うーん、これはむしろUU learningでは？)すべての候補遺伝子を確認するのは大変だが、PUによって、有望なサブセットを絞り込むことができる。

• タンパク質複合体のような、相互作用するタンパク質の集合での予測でも使える。既知の複合体をPositive、それ以外をUnlabeledにしているという形。
• 遺伝子調節ネットワークは細胞機能を制御する遺伝子の集まり。ここでも同様にできるらしい。(具体は書いてない)
• 製薬でも、薬剤と疾患の相互作用を探るペアで、ペアワイズスコアリングベースの方法のPUも考えられる。
• 種の生息地のモデリング(見つかった=positiveだが、見つからなかった=unlabeled)
• ターゲットマーケティング(買われた=positiveだが、買われなかった=unlabeled　買われなかったからと言って好かれなかったのではない)
• 衛星画像での各ピクセルの所属するカテゴリ(森、市街地etc)の分類(多クラスといえる。Ishida 2017のようにラベル付けが大変な場合の補ラベル学習ができる)
• レコメンドシステムにおける不正直な肯定or否定の分類(positiveとしていくつかの不正直な投稿が与えられ、他はUnlabeled)
• ウェブクローラーで訪問するかどうか(訪問したほうがいい例を提供する=positiveだが、明確に訪問するべきではないnegative例の提供は難しいので、残りはUnlabeledとして扱う)
• 時系列データの異常検出(いくつかの手動で見つけたパターンをpositiveとして扱い、それ以外のすべてをunlabeledとする)

ラベルつきとラベルなしのデータから自分で学習するのが自己教師あり学習。すべてのクラスのラベル付き例がデータに存在すると仮定されている。しかし、PUでは一方しかない(つまりPNUの設定である)。

クラス事前確率を使う手法は、自己教師あり学習でも有効。

異常値検出のように。負のクラスがほかのすべてのクラスから成る二値分類器だとする。

基本的にはデータにはラベルがないのでUnlabeledになって、そこからがんばっていくつかPositiveをつけてPU Learningを行うようである。SCARだとやりやすい。

PositiveをNoisyじゃないPositiveとして、それ以外をNegativeとして扱う手法といえる。

欠損データ補完から得られたSAR,SCARなどのように、これも分類できる。

• NCAR　ノイズが完全にランダム。すべてのクラスラベルは例によらず、誤る確率は等しい。
• NAR　ノイズはランダムだが、誤る確率は真のクラスに依存する。
• NNAR　ノイズはランダムで、誤る確率は真のクラスとデータ自身の両方に依存する。(あってる？)

誤ラベル率はノイズ率、フリップ率と呼ばれる。

PUにおけるSCARはNCARに相当。もっと言えばこれはNARからの一般化なので、そこら辺の手法を適応できる。

欠損メカニズムといって、どの世いう名値が欠損しやすいのかが重要これも仮定がある。

• MCAR　完全にランダムに欠落していく。
• MAR　ラベルの欠損確率は、観測可能な属性(所属クラスなど)に完全に依存する。
• MNAR　ラベルの欠損確率は、欠落している値に依存する。

SCARもSARもMNARに属する。

バッグ内にPositiveが1つでもあればPositive, そうでないならNegativeとして学習する。これも一種類のPUといえる。

1. SCAR仮定で多くの研究が進められているが、SAR仮定がより現実的。いろんなシチュエーション考えてやってみようや。
   1. 難易度を落としたものとして、確率密度が特定の範囲で0か非常に小さい値をとるという場合を考えるのはいいかも。
2. みんな使っているモデルやデータセットがばらばらになりがち。広範囲的な評価を行って、どのような手法が好まれるかを決める (Ohtaさんのやつかな)
3. PUの汎化性能評価では、PN Learningでの性能との差をみるが、PUから学習するという動機に合致しないのではないか。PUで比較するような指針もあるがSCARばかりであってなかなかに困る。
4. 実世界のデータはやはり予想外が起きるので、何かの予想外によってPUの学習アルゴリズムのい性能が壊れるようなことがあると面白そうだ。

最近、関係性データからのPUに再び注目が集まっている=知識ベースの補完のように。