JMLR-2022-On Mixup Regularization

https://www.jmlr.org/papers/volume23/20-1385/20-1385.pdf

Mix-upは2つのサンプルの内分点を取って生成するData Augmentationである。CIFAR-10の画像なら以下のように。ラベルも同様に内分点で合成していく。

この論文では、理論的な裏付けを考えた。

Introduction

この論文では、Mixupとは以下の組み合わせであると主張している。

データの変形
ランダムな摂動を加える

訓練時にデータをmix-upをするが、画像処理のNormalizationなどについては、平均などがかかわる。ならテスト時にも(予測結果を使わないにせよ)mix-upしてから予測するべきでは？→そういう時もある。

何故うまく行くか？→理論的にLabel Smoothingとリプシッツ定数を抑えられるから。

陽的正則化という、明示的な罰則項やバッチ正則化、ノイズを加える(これはL2正則化と同じ効果を持つらしい)など意図的な正則化と、陰的正則化という明示的にやってないDropOutや重みの共有などがある。後者がうまく効くので、大量のパラメタがあるDNNも実用的である。

MixupやLabel Smoothingは同じように、出力確率のCalibrationに有効である。本質的に同じやつなんじゃないか？入力ノイズにも強いが、これはDropoutと同じ原因があったりする(これの証明と同じようにやっている？)？GANの学習でMixupを使うと安定する。ここら辺の話からリプシッツ定数が抑えられているのでは？と思っている。こんな疑念が出てくる。

以下が他の正則化との比較。Mix-upが関係するものは以下のようなものである。

結果から言うと、Mix-upは以上の手法のもたらす効果のすべてを兼ね備える。

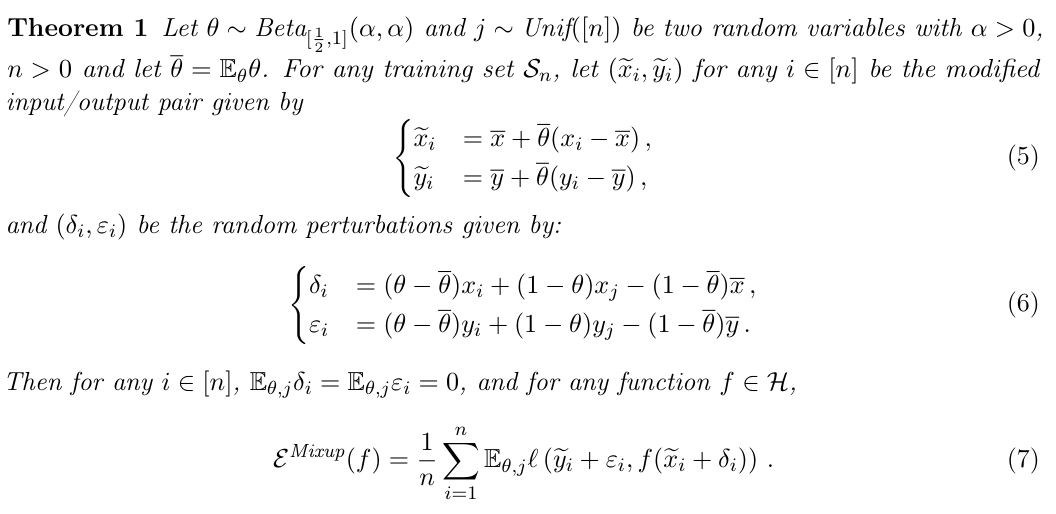
Beta分布を右半分の $[1/2,1]$ しか取らないようにしても、 $\mathbf{x}_i, \mathbf{x}_j$ を交換すれば同じことができると考える。そして、 $\tilde{x}_i, \tilde{y}_i$ は、平均点へ少し近づけた点(これが摂動とみなせる)である。そして $\delta_i, \epsilon_i$ は平均点へ少し近づけた点から、本来のmixupの作られる点にするための増分である。(これはただ式変形しているだけ)

$\delta_i, \epsilon_i$ の期待値は0である。 $(\theta - \bar{\theta})$ は収束するので0に、 $\theta, x_i$ はそれぞれ独立に期待値に収束するので、 $(1 - \theta)x_j - (1 - \bar{\theta})\bar{x}$ の期待値も0なので全体で0。

ということで、非常に面白い結果として、

$\tilde{y}_i$ はLabel Smoothingをしてそう。
$\delta_i$ は期待値0で何かしらの分散を持つ摂動っぽそう。

という結果になる。

Mix-upの正則化効果

l(\tilde{y_i} + \epsilon_i, f(\tilde{x_i} + \delta_i))

これをテイラー展開して、二次までやる。Dropoutの正則化の効果の証明に、二次までが使われていたので。

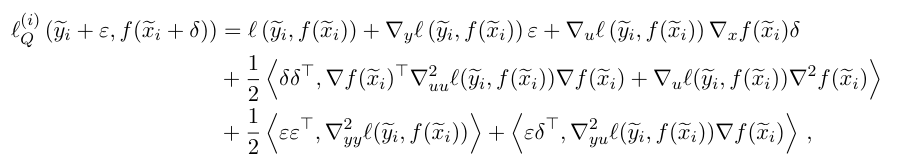
これは、本体(サンプルもラベルも平均に少し近づけた)の学習と、正則化項とみなせる。すると、最後の項について、 $\epsilon \delta ^ T$ と言う形が出てくる。これはMix-up特有のサンプル $\mathbf{x}$ もラベル $y$ もお互いに関係を持つ象徴である。Dropoutはサンプルだけにかけているし、Label Smoothingはラベルにだけ欠けていたのと対照的に、全部にかけているのがMix-upだと数式で改めて分かった。

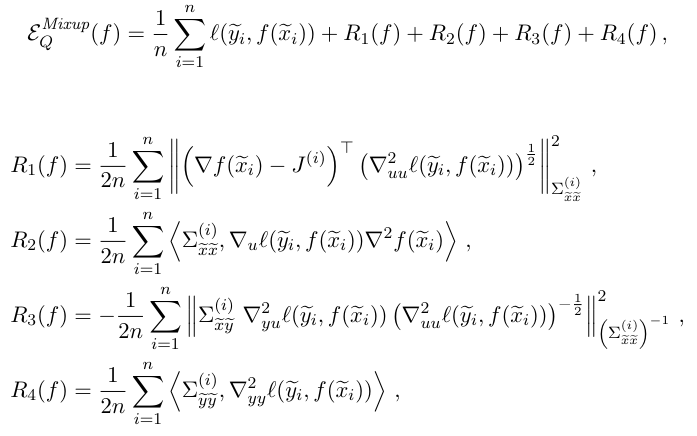
経験的に式を書き直すとこういう感じ。この4つの項を学習でできたら、Mix-upと同じ効果を(二次近似の場合で)持つ。

実際の実験では、 $R_2$ は計算しづらいので消したらしい。近似の精度が良くないので消すと困るはずだが、予測精度は不思議にも下がらない。つまり、この二次近似は十分に正しい。

上の経験的な式を元に、実験をした。左が正則化項の値( $R_1+R_2+R_3+R_4$ )であり、右が $1/n \sum_i ^ n l(\tilde{y_i} + \epsilon_i, f(\tilde{x_i} + \delta_i))$ 。

赤がサンプルとラベルに何もしない、青がサンプルとラベルをMix-up。ピンクはサンプルとラベルについて縮小データ $\tilde{y_i}, \tilde{x_i}$ の変換をして学習する。

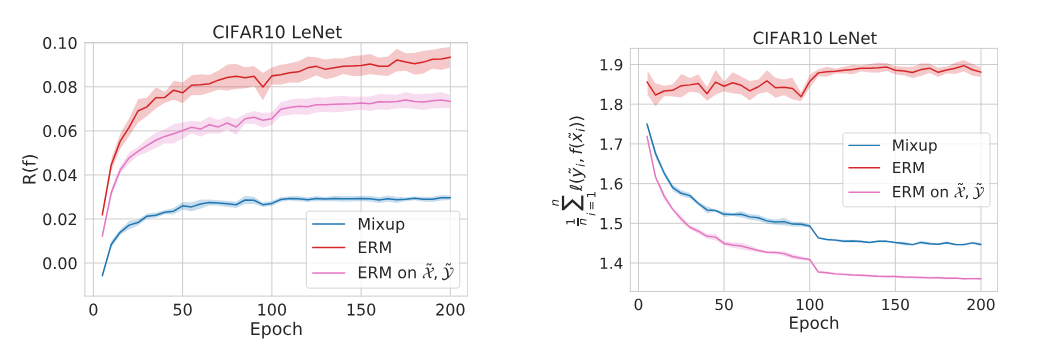
以下のことがわかる。

縮小データ $\tilde{x}_i, \tilde{y}_i$ についての損失は、何もしない<<Mixup(縮小+ランダム摂動)<縮小データ
正則化項については、何もしない<縮小データ<<Mixup(縮小+ランダム摂動)
Mixupはちゃんと変形させて出てきた(二次近似の)正則化項も、本体も低下をさせていた。
ピンクは本体は過学習しているように見える(正則化項を甘利は低下させてない)。でも何もしないよりは効果が出ている。

このように、Mix-upは、サンプルとラベルを平均方向へ縮小させる+ランダムな摂動を加えるに相当する。それで訓練を施したのならば、テスト時にもサンプルとラベルを平均方向へ縮小させてから、判定結果を(ラベルの平均と)縮めたのを戻す必要があるのではないか？

以下の式は平均へ縮小させたサンプルによる予測結果を、 $1 / \bar{\theta}$ の拡大によってラベルの平均と戻した。

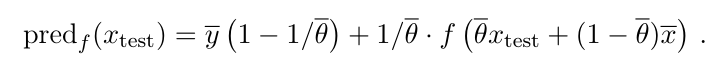
この変換について、ReLUが活性化関数で、斉次のモデル( $y=ax+b$ が例。 $x, y$ を $\theta$ 倍したとしても斉次なら意味はない)では意味がない。しかし、それ以外では意味があるとちゃんと示せた。(ちょっとだけ)

ただ、 $\bar{x}, \bar{y}$ が必要であるので、平均が変わってしまうと逆変換をやると逆にoverfittingして困る。

最後に、自信過剰な推定について。

Label Smoothingをおこなうことによって、確かに改善できる。では、Mix-upはどうか。

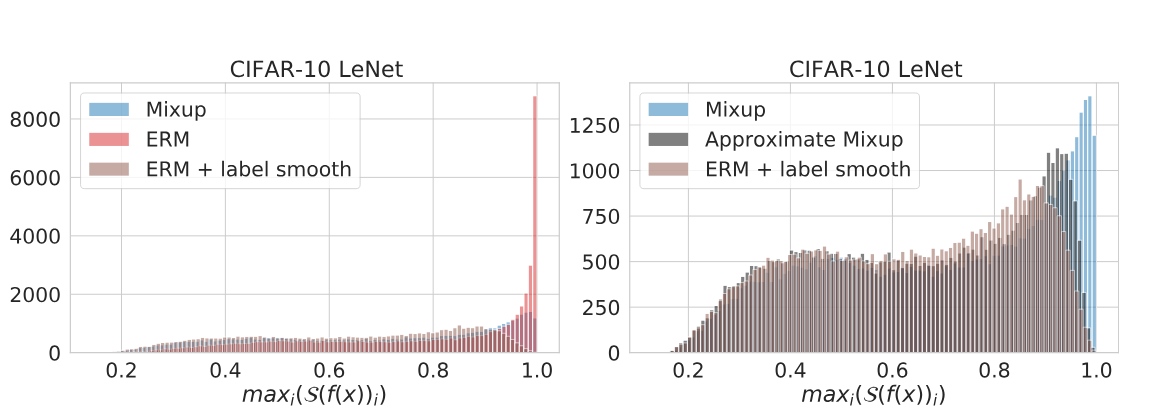
なにもしないと予測結果が自信過剰になるが、Mix-upはLabel Smoothingのと何もしないのと同じくらいの効果が得られる。

同じクラスをMix-upしてもラベルはあまり変わらないので、ちゃんと違うクラスをmix-upするべき。

Sen(Qian)’s Memo