https://arxiv.org/abs/2011.04406
Introduction
各サンプルが独立して一定確率で間違えるとき、いかに間違いなく学習できるかというのがNoisy Labelの問題。ノイズ率が1/2以下であれば、何かしらのアルゴリズムが存在してNoisy Labelの問題に対処できるという。
この論文では、 がノイズある分布から得られるサンプルだとする。
Noisy Labelでは、浅い学習と深層学習それぞれが主流の2つの時代がある。前者では、Statistical Learningで不偏損失関数を設計しなおすLoss Correctionが主流だった。深層学習が主流の時代は、Representative LearningでDNNの記憶を利用する手法やバイアスある損失関数を利用するものもでてきた。そして、深層学習におけるNoisy Labelはまだ研究として未完成な分野である。
Label Noise Statistical Learning(LNSL)とLabel Noise Representative Learning(LNRL)は同じ問題設定の問題を解くが根本的には異なるもの。
Related Literature
いかに重要な研究を載せる。
Early Stage
- はじめて二値分類における、Noiseを考慮した不偏リスク推測の式を提案した。各サンプルが独立にノイズを含みうる状況下での学習において、リスクを最小化することで分類できると証明したはじめての研究。
N. Natarajan, I. S. Dhillon, P. K. Ravikumar, and A. Tewari,
“Learning with noisy labels,” in NeurIPS, 2013
2015年以降、Label Noise Representative Learningへどんどん移行していった。
Emerging Stage
LNRLでは、古典的なノイズ変換行列、正則化、損失設計は依然として有効。
Flourished Stage
研究が盛んになってきた時期。
Overview
問題定義
ノイズ入りの訓練サンプル とノイズなしのテストサンプル がそれぞれ存在し、前者から学習することでうまく後者に対してfittingをしたい。それぞれ、 というノイズ有の分布と というノイズなしの分布から得られている。
理想的なベイズ分類器は であり、これに近似するために仮説空間 に含まれる、パラメタ によって制御される仮説たち がある。仮説空間 の中で最も妥当な は とする。
このとき、NLRLは からうまく を定めて、 を見つけるというのが最終的なゴール。
具体例でいうなら、大量の音声コーパスから訓練されたAppleのSiriや、十分なデータで訓練することで得られるDNNによって、悪意ある攻撃から計算機を防ぐなど。敵対的サンプルもあるが、これもAdversarial Trainingを重ねることで改善することがわかっている。
だが、LNRLはそもそも不正確な訓練サンプルから訓練する手法。具体例としては以下の3つがある。
- 大量の画像で学習する場合。大量の画像のラベル付け自体は大変でノイズがある程度混入されていると仮定するべきである。
- ヘルスケア。非常に属人的で、専門家によるラベル付けをもってしても主観を取り除けずに誤ったラベル付けが発生することが往々ある。しかも誤り率が非常に高い。
- 音声認識。電話対応の評価について評価者の心情などに大きく依るのでそもそも誤り率が非常に高い。
そのうえ、LNRLでDNNを使うにあたって、DNNの学習能力が高すぎて、ノイズまで学習してしまうという特徴が得られる。
周辺の学術領域との違い
- Semi-supervised Learning。多くのラベル不明のデータを自己判断でラベル付けして学習を進めること。しかし、完全にCleanなデータが一部でも与えられるのがNoisy Labelと違うところ。
- Positive-unlabeled Learning。UnlabeledはNoisyだとみなせるが、Positiveは常にCleanであるという点でNoisy Labelとは違う。
- Complementary Learning。○○ではないという補ラベルでの学習。しかし、遷移行列の対角成分は常に0であるという制約があるのに対して、Noisy Labelでは存在しない。(絶対○○ではないというのを遷移行列で表現するとそうなる)
- Unlabeled-unlabeled Learning。異なるPositiveとNegativeの割合=class priorを持つ2つの集団について学習をするという問題設定。ただし、しかし、class priorという情報を持つという点で異なる。
このようにNoisy Labelの問題設定は非常に厳しく、何かしらの仮定を加えてじゃないとやるのが難しいということがわかる。
Noisy Label条件下での経験誤差
損失はNoisy Labelの一般的には以下の形となる。
そして、これは経験的な損失については以下のようになる。このような損失関数 を設計するのがNoisy Labelのやりたいこと、と捉えられる。これが見つかれば、後は通常の最適化手法を適用すればよい。
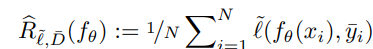
理論的理解
以下の3要素からとらえて考える。
- データ。どのようにデータにノイズが入っているのか(どれほどの確率でクラス から になるのか、のような遷移行列を推測したいのがベスト。これがわかれば、損失関数も簡単に書き換えられる)
- からノイズを考慮した を設計する。正則化を加えることにより、ノイズにロバストになるようにすることができる。bootstrappingやAdversarial Trainingなどでね。具体的な の設計は以下の選択肢がある。
- 線形に正則化項を足す。
- 何かしらの重みによる線形合成。
- それ以外
- 最適化のやり方。DNNなどの記憶する特性などを用いて、ノイズをうまく記憶させないようにする。
- DNNのMemorization Effectに頼ることで、DNNは簡単な=ノイズが入ってないパターンを先に記憶し、そののちに複雑なNoisyなパターンにOverfittingすることがわかっている。
- このことから、簡単なもの=小さい損失を持つサンプルのみ誤差逆伝播で更新すればいいという考えになる。ノイズが混入する率が だとっするとき、損失が小さい順に並べた時の上位 はノイズが混入されてないと考えて、それらだけ誤差逆伝播で更新するという考え。
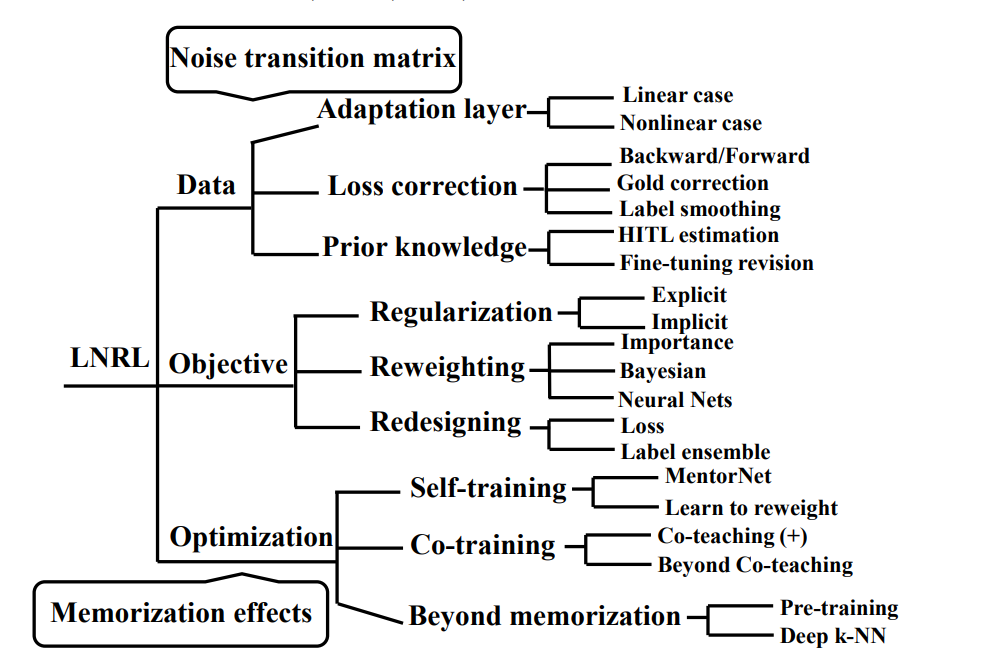
データ
ノイズには
- Instance依存ノイズ。 。同じground-truthのクラスでもインスタンス に依存する。ノイズ遷移行列は と書くことに。
- Instance独立ノイズ。 。同じground-truthのクラスならインスタンスに限らず一定。こっちの方が明らかに問題設定としては簡単。ノイズ遷移行列は でOK。
ノイズ遷移行列を推定するには、絶対にクラス○○で間違いないサンプルをアンカーとして用いる。 であるのが前提。
これを用いると、クラス から へ間違う確率 を設計できる。アンカーであれば、 以外の全ての に対して なので、こうなる。
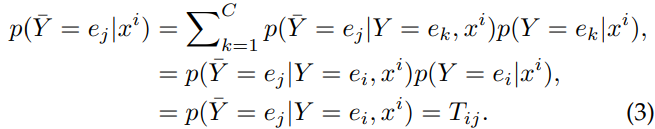
もし、アンカーがわからないのであれば、 が最も大きいものを選ぶなどすればいい。
このようにしてつくられた遷移行列 は、 が得られる。これはInstance独立ノイズにおいては最終決定版と言えるぐらい強力な式。
よりロバストな場合、信頼できるサンプルのみで を作ることもある。
この は、損失補正などで使われたり。
対象の損失関数
層あるDNNについて、一様大数の法則でしっかりと収束が証明できるという話。カット。
最適化における戦略
ロバスト性を保つためには、DNNの訓練のearly stoppingが必要という話。
Dataでのapproach
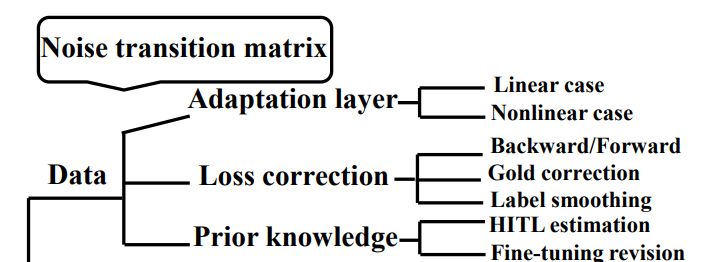
この図がDataでのアプローチについてまとめている。遷移行列 の構築や推定を以下にするのかという考え。詳しくは以下の3つのアプローチがある。
- DNNの最後に層を追加することで を実現する。
- を経験的に推定し、それをもとに損失関数のクロスエントロピー損失を修正する。
- 事前知識をもとに推定する。
Noise変換行列とは
がクラス がクラス になる確率を示している行列。インスタンス に依存する場合としない場合がある。ありうるモデルとして以下の2つがある。
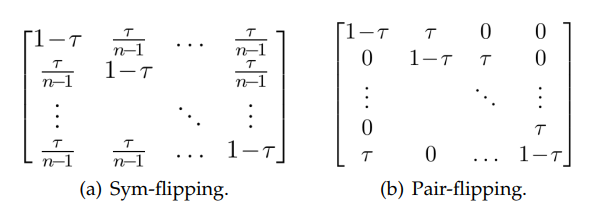
- Sym-flippingはすべてのクラスで で正しく、それ以外に等確率で間違うという仮定。
- Pair-flippingはすべてのクラスで で正しく、それ以外はクラスから へのみ の確率で動くという仮定。
- 1つに限らず、より近いクラスにしか間違われることがないという意味。
ただ、現実は複雑であり、不規則な遷移行列となることはしばしばある。Clothing1MといTaobaoのデータセットなど。
への推定し方法として、以下のようなものでできるが、信頼できるアンカーがなかったりするので前述した3つのカテゴリの手法が使われていたりする。
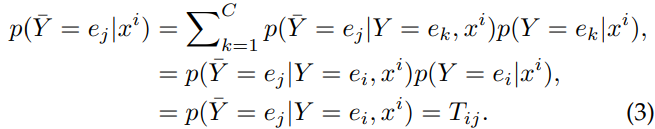
DNNの最後にAdaptation Layerを追加
DNNの最後に層を追加することで、 の役割を果たしてもらう手法。そもそも であるので、設計思想としては非常に筋が通る。
線形層だけを追加するならば、まさ を作ることに相当する。ただし と本来のパラメタと同時に誤差逆伝播では、 を最適化するのは難しいということで、 のtraceやリッジ回帰の正則化を加えた の最適化を行っている。
実際の操作は を乗じるのに相当する。
謎: まずパラメタを訓練して、そこから凍結して を訓練したほうが本来の の定義上望ましく、おそらくそうしている。読んでみないとわからない。
論文: S. Sukhbaatar, J. Bruna, M. Paluri, L. Bourdev, and R. Fergus,
“Training convolutional networks with noisy labels,” in ICLR
Workshop, 2015. https://arxiv.org/abs/1406.2080 refer:690
損失の前に非線形層を追加するという手法がある。学習するデータはNoisyなGround-Truthしか持たないので、ここで、モデル本体 と追加した非線形層 の訓練はちょうどEM-Algorithmで行うことができるというのを利用して訓練した。(インスタンス独立ではない場合、非線形層を追加することで表現力が上がって結果的にfittingしやすくなるかも?)
ただし、EMアルゴリズムは局所最適解に陥ったり、データが増えると性能が低下するという問題を抱える。よって、最適化で2つのモデルを提案した。
- Sモデル。見えない潜在的な真のラベルのみでNoisyなラベルが何になるかを予測するする学習。EMアルゴリズムで最適化できる。
- なので、 と は交互に最適化するので、同時に最適化をやっているというわけである。
- Cモデル。潜在的な真のラベルのみならず、インスタンス にも依存してNoisy並べるが何になるかを予測する学習。
- これもEMアルゴリズムで学習しているはず。だが、より難しいとのこと。
論文: J. Goldberger and E. Ben-Reuven, “Training deep neural-networks
using a noise adaptation layer,” in ICLR, 2017. https://openreview.net/forum?id=H12GRgcxg refer:682
損失較正
損失関数を修正することによって、Noisyな入力にも強い損失を作る取り組み。
Noisyなサンプルに対しても、もしCleanな時の損失関数 が取る値と同じような値をとる を設計するのが目標。
さきほどのデータは「変換してからロスを出す」だったが、こちらは「ロスを出して変換する」設計思想。
forward/backward correction
backward correctionは、正則な遷移行列 を持つとして、以下のNosiy向けの損失であるである。原文ではベクトルの定義に転置が抜けているので注意!(参考先は転置があった)
定義からして、 (それぞれ列ベクトル)であるので、 であり、これを用いたかたち。 はベクトルの 番目の値の抽出を意味する。
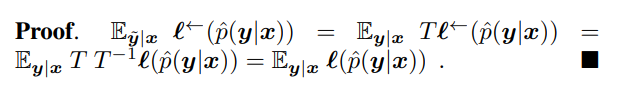
つまり、損失を出してから変換する。注意点として、線形変換を行う以上左辺が0未満になる可能性もある。
forward correctionは同様に があるとして、以下のNoisy向けの損失である である。
ここで、 は先ほどの予測したlabelのみと異なり、各カテゴリへの予測の確率であるというもの。といってもDNNなら簡単にsoftmaxから得られるが。
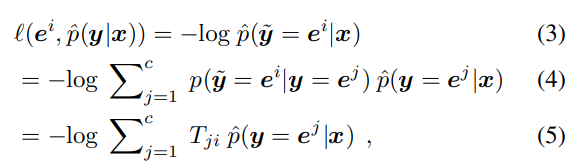
Cross-Entropy損失の性質上計算するとtransposeが得られる。これについて、 となるとわかる。

証明は という単一のラベルを カテゴリについてそれぞれのクラスの予測確率のベクトルに変換する写像。Noisサンプルに対しての損失は、 で合成写像を作ればいい。式(9)では、Noisyなサンプルについての期待値の最小化=学習を行うと、Noisyなサンプルについての較正された確率が得られる。あとはNoisyなものに対しての較正後に変換をするという式となる。(なので (10)の適用の順番は では、と思っている)
- データにAdaptation Layerを追加するのは、確率に較正される前に変換を施すこと。
- forward Correctionは確率に較正された後に変換を施すこと。
- backward Correctionは確率に較正されてlossにも入れた後に変換を施す。
論文: G. Patrini, A. Rozza, A. Krishna Menon, R. Nock, and L. Qu, “Making deep neural networks robust to label noise: A loss correction approach,” in CVPR, 2017, pp. 1944–1952. https://arxiv.org/abs/1609.03683 refer1460
Gold Correction
大量にNoisyなサンプルが存在するとき、変換行列の推定が難しくなる。Gold Correctionは、一部の信頼できるサンプルのみを使って、変換行列 を推定する方法。そして、その推定した を用いて全体のDNNを訓練するということになる(訓練のやり方は前述や後述の各手法となる)。つまりこれは独立して扱うことができる手法。
推定自体は、アンカー自体は不要で(というか全部明確にわかっているのでアンカ全体の集合だけで計算しているともいえる)、以下のように計算できる。
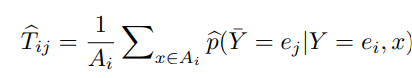
論文: D. Hendrycks, M. Mazeika, D. Wilson, and K. Gimpel, “Using trusted data to train deep networks on labels corrupted by severe noise,” in NeurIPS, 2018, pp. 10 456–10 465. https://arxiv.org/abs/1802.05300 refer571
Label Smoothing
ラベルに一様分布に属するベクトルを加える事で、全体的にロバストにすることができる。例えば、正解が ならば、 にぼかすことを指す。 というSmearing Matrixを介してNoisyなものへと遷移する。
lossのあとに変更するので、Backward Correctionの一部であるでもある。
- なら、Noisyが全くない。
- 。ここで であり、 はクラスの数。 は全部の成分が1の行列。
- 。これは対称なNoiseらしい。よくわからない…
論文: C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens, and Z. Wojna, “Rethinking the inception architecture for computer vision,” in CVPR, 2016. このCSDNがおすすめ
論文: M. Lukasik, S. Bhojanapalli, A. K. Menon, and S. Kumar, “Does label smoothing mitigate label noise?” in ICML, 2020. http://proceedings.mlr.press/v119/lukasik20a.html?ref=https://githubhelp.com refer307
事前知識
を推測するのに、人間の事前知識などを使う。
Human in the loop
人力で を作る(catとcarは間違えやすいなどなど)。往々にして、Column-diagnal行列、幅3の対角行列、ブロック対角行列のような形となる。これらを組み合わせて、ターゲットの行列を作り上げていく。
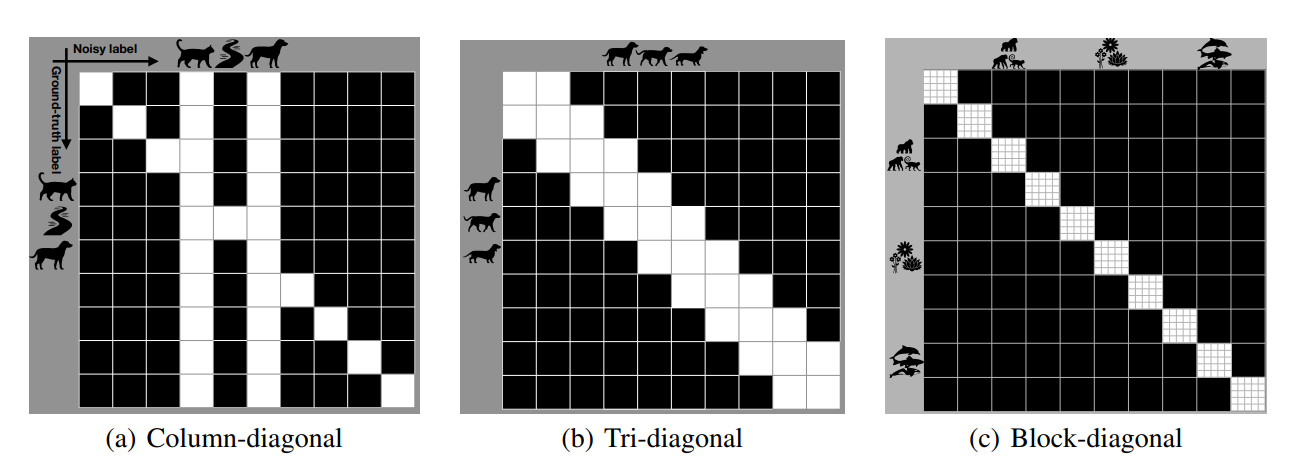
以下のステップを踏む。
- のGround-Truthを考える。これは潜在的なので実際にわかることはない。
- 先ほど人力で作り上げたものを を満たす条件の写像 で 人力の から への写像である。
- の遷移行列をサンプリングする。これはDNNから得られる、明示的ではない構造をもつもの。
- この こそが求めていた遷移行列。
論文: B. Han, J. Yao, G. Niu, M. Zhou, I. Tsang, Y. Zhang, and M. Sugiyama, “Masking: A new perspective of noisy supervision,” in NeurIPS, 2018, pp. 5836–5846. https://arxiv.org/abs/1805.08193 refer240
Fine-tuning Revision
アンカーのサンプルに似た、間違っている確率が高いサンプルで遷移行列を作る。
- ノイズある訓練データセット をそれぞれ用意する。
- 普通にDNNで学習することで、 を得られる。
- このNoisyなものの中からで各クラスごとに信頼度が最も高い をアンカーとして、遷移行列 を作ってみる。これを初期値として、 を更新していく。
- を
- 当初のDNNについて、をAdaptation Layerに(おそらくLinear層として)追加(それとも と書いてあるので、Forward Correctionかは論文を読んでみないとわからない。)しそこで再び損失を最小化するように学習を進める。
このように学習を行う。
論文: X. Xia, T. Liu, N. Wang, B. Han, C. Gong, G. Niu, and M. Sugiyama, “Are anchor points really indispensable in label-noise learning?” in NeurIPS, 2019 https://arxiv.org/abs/1906.00189 refer331
損失関数の修正でのapproach
大きな方向性は正則化項を加える で正則化するのと、重みを動的に決定していく で正則化するのと、アルゴリズムレベルから弄る(ドロップアウトみたいな ドロップアウトが必ず有効というわけではない)実質その他の3つがある。
正則化項を加える
明示的な項を持つ正則化
グループ正則化という、いくつかの畳み込みフィルタによる畳み込み結果=チャンネルをまとめて、それを正則化するもの。
グループ正則化を施すと有効らしい by Azadi よくわかりませんでした…
論文: S. Azadi, J. Feng, S. Jegelka, and T. Darrell, “Auxiliary image regularization for deep cnns with noisy labels,” in ICLR, 2016. [21] J. Goldberger and E. Ben-Reuven, “Training deep neural-networks using a noise adaptation layer,” in ICLR, 2017. https://arxiv.org/abs/1511.07069 refer90
また、MixMatchという手法がある。Minimum Entropy Regularizationという、正則化項にエントロピー を加えるもの。加えることにより、Unlabeledなものに対してはペナルティを追加することで、明確な分類を促進させることができる。
論文: D. Berthelot, N. Carlini, I. Goodfellow, N. Papernot, A. Oliver, and C. A. Raffel, “Mixmatch: A holistic approach to semi-supervised learning,” in NeurIPS, 2019. https://papers.nips.cc/paper_files/paper/2019/hash/1cd138d0499a68f4bb72bee04bbec2d7-Abstract.html refer3000over
MixMatchとは異なるけど結果的に同じ事をやる手法として、確度が高い不明なラベルにラベルを割り当てる事ができる。(自己教師アリ学習あるある)これも明らかに分布を極端にする作用を持つ。この操作を写像の適用と考えることもでき、より分布を鋭くすることから、sharpning functionと言われたりする。
論文: D.-H. Lee, “Pseudo-label: The simple and efficient semi supervised learning method for deep neural networks,” in ICML Workshop, 2013. https://www.researchgate.net/publication/280581078_Pseudo-Label_The_Simple_and_Efficient_Semi-Supervised_Learning_Method_for_Deep_Neural_Networks refer3895
局所の滑らかさ=入力が少しnoise入っても出力が大きく変わらない性質、をうまく利用することで改善できる研究もある。
は分布間の距離で、 はサンプルの特徴量(一部でも全部でもよい)、 はモデルパラメタ。
は だけ入力がどのようにずれても、ありうる最大の分布の距離となるような 。つまり最悪のケース(Adversarial Exampleっぽいので、Adversarialという名前に)。
最悪ケースを引いても、分布の距離はどれほど遠くなるか、という指標。
そして、これを使った正則化項としてこのようなものがある。
はラベルが完全にあるもの。 はラベルが不明なもの。すべてのサンプルに対して、LDSを計算している。そして、それを通常の だけを使って計算した損失と合算する。
論文: T. Miyato, S.-i. Maeda, M. Koyama, and S. Ishii, “Virtual adversarial training: a regularization method for supervised and semi-supervised learning,” TPAMI, vol. 41, no. 8, pp. 1979–1993, 2018. https://arxiv.org/abs/1704.03976 refer2795
明示的な項を持たない正則化
Bootstrapを利用したBagging
Bootstrap自体ロバスト性を高めるので、Noisy Labelでも有効。エントロピー最小化の項と同じである。
通常のエントロピー最小化と、与えられたラベルのハイパラ による混合によって、ノイズへの強さと曖昧な確率分布へのペナルティを両立させる。
hardなロスもある。
ここでは、混合するときの が最大のものだけ1となり、それ以外が0になるなどと分布をとがらせている。hard版を解決sるとき、EMアルゴリズムを使うらしい。
論文: S. Reed, H. Lee, D. Anguelov, C. Szegedy, D. Erhan, and A. Rabinovich, “Training deep neural networks on noisy labels with bootstrapping,” in ICLR Workshop, 2015. https://arxiv.org/abs/1412.6596 refer1103
Mix-up
サンプルを混合させて新たなサンプルを作りだすdata augumentationの手法として有名。
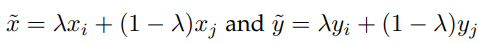
このようにサンプルもその(Noisyな)ラベルも混合させる。
SIGUA
勾配降下法では過剰にノイズにもoverfittingしてしまう問題について、勾配を逆に登ってみればいいのでは?かしこい
stochastic integrated gradient underweighted ascentという、良いデータでは通常通り勾配を降りるけど、悪いデータでは勾配を上げることが大事。一部のmini-batchに対してのみ行うのがSIGUA。parameter-shrinkingはすべてのデータに対して勾配を上げる。
論文: B. Han, G. Niu, X. Yu, Q. Yao, M. Xu, I. Tsang, and M. Sugiyama, “Sigua: Forgetting may make learning with noisy labels more robust,” in ICML, 2020. https://proceedings.mlr.press/v119/han20c.html refer103
Reweighting
損失関数を のかたちで重みを変えていく手法。
ほかにも、サンプルごとに重みを変えていく手法がある。
重要度 Reweighting
ドメイン適用から来た考え方。Noisyなサンプルはソースドメイン、Cleanなサンプルはターゲットドメインとして扱う。

展開して、分母分子共に同じものを乗じて、同じ条件付確率にしてから、 という分布の変換関数を用意している。この をいかにして学ぶのが重要。
論文: T. Liu and D. Tao, “Classification with noisy labels by importance reweighting,” TPAMI, vol. 38, no. 3, pp. 447–461, 2015. https://arxiv.org/pdf/1411.7718.pdf refer891
ベイジアンモデル
コンセプトはNoisyなラベルの重みを下げて、Cleanなラベルの重みを上げる。重みとラベル出現をつかさどる変数はいずれも指定の事前分布から得た。
- 潜在変数 をおく。それによって、データのラベルがそうなるときの尤度はお互いが独立した志向なので、 となる。
- ここに、各 の尤度ごとに重みを追加する。重みはそれぞれ の潜在変数を持つとする。
これを導入すると という式に。 は正則化係数。
- を推定する。前提知識としての候補としてはβ分布、スケール下ディリクレ分布、γ分布などがある。
他にも、Cleanな損失 とNoisyな場合の損失 をそれぞれ一定比率で混合するやり方がある。β分布をそれぞれの分布のモデルとするらしい。
Neural Network
Meta Weight NetというDNNを使い、サンプルの損失からそのサンプルの重みをどうするべきかを推定する。
このDNNの訓練には一部の絶対にCleanなデータを使って行う。
論文: J. Shu, Q. Xie, L. Yi, Q. Zhao, S. Zhou, Z. Xu, and D. Meng, “Metaweight-net: Learning an explicit mapping for sample weighting,” in NeurIPS, 2019, pp. 1919–1930. https://arxiv.org/abs/1902.07379 refer753
再設計
そもそも損失の形を再設計する。
loss関数の再設計
平均絶対誤差のノイズに対しての頑強さとクロスカテゴリエントロピーの間違ったものに対してペナルティをある程度大きくする双方の利点を兼ね備えた損失がある。
であり、 はone-hotベクトル。 は学習器の 番目の成分つまりラベルが である確率である。 とすればクロスエントロピーに、 とすれば平均絶対誤差である。これはBox-Cox変換という有名な分布を無理やり正規分布に近づける手法。
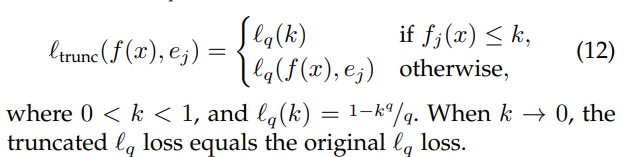
実際に使う時は異常のように、ハイパーパラメタの によって切り替えることで、あまりに大きな損失を出さないようにすることができる。
📄2018-NIPS-[GCE]Generalized Cross Entropy Loss for Training Deep Neural Networks with Noisy Labels
が定数である、対称的な損失だといいという研究もある。PUのDu Plessisも同じようなこと言ってましたねぇ!次のような損失を提案した。
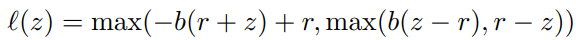
論文: N. Charoenphakdee, J. Lee, and M. Sugiyama, “On symmetric losses for learning from corrupted labels,” in ICML, 2019. https://proceedings.mlr.press/v97/charoenphakdee19a.html refer102
学習する際に、よろしくないサンプルを学習させないように損失関数を設計する手法もある。グあ知的には、 クラスの分類ならば、 クラス目として「棄権」=分類に参加させないというのを設ける。損失としては以下のを定義する。
前半はクロスエントロピー誤差を改造したものと考えられる。棄権させる場合の確率の正則化させてからのクロスエントロピーである。後半は棄権に対するハイパーパラメタ で制御されるペナルティ項である。この手法(DAC)は構造があるノイズもないノイズにも有効。
論文: S. Thulasidasan, T. Bhattacharya, J. Bilmes, G. Chennupati, and J. Mohd-Yusof, “Combating lab https://arxiv.org/abs/1905.10964 refer117
自信が過ぎることによる学習のやり過ぎで、Gradientの最大値を制限する手法もある。Huber損失というものを元にしている。
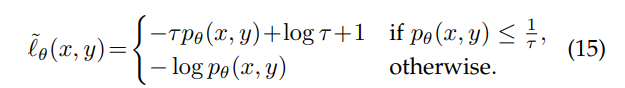
これによって、ラベル判断の確率 が小さいときに取る損失を小さくすることができる。
論文: A. K. Menon, A. S. Rawat, S. J. Reddi, and S. Kumar, “Can gradient clipping mitigate label noise?” in ICLR, 2020. https://openreview.net/attachment?id=rklB76EKPr&name=pdf refer137
損失関数が常に01損失よりも過分に判定する(1を超える)場合、以下のような01損失の改良版を使うことができる。これによって、過分に判定という問題を改善することにもつながる。 は識別器による判定して得た値で、 のGround-Truthのラベル。
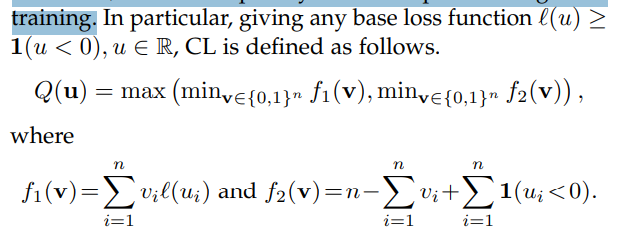
この損失関数の性質としては以下のようによりタイトな評価上界を持つということ。
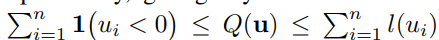
この損失単品ではノイズに対してどうということではないが、ほかのNoisyっぽい学習データを選別的に学習させないことによる手法と組み合わせることもできる。
論文: Y. Lyu and I. W. Tsang, “Curriculum loss: Robust learning and generalization against label corruption,” in ICLR, 2020 https://openreview.net/forum?id=rkgt0REKwS refer160
ラベルアンサンブル
複数個の識別器による結果をアンサンブルするのはNoisy Labelにも有効。
Laineらは2つの手法を提案。Pi ModelとTemporal Modelである。

πモデルでは上記のようになる。
各mini-batch (Cleanなラベルが存在するもの)に対して次のようにする。
- に対してあるaugmentationを施した をそれをdropoutした識別器に入れて、予測する。 =
- に対して同じアルゴリズムだがランダムで違うaugmentationを施した を得て、それを別のようにdropoutした識別器に入れて、予測する。
- 次のような損失を計算。
前半はground-truthとのクロスエントロピー誤差で、後半はaugmentedされたデータ同士の識別の二乗誤差を0に近づけるため。 は時間依存の重みで、 は分類カテゴリ数。
上のように2回もランダム的にデータに変動、識別器に変動をさせることで、人工的にノイズあるデータを生成したとみなせる。本来のラベルと一致するように学習をさせつつも、その2つの識別器の結果が同じになるように訓練したいというモチベーション。
なお実験では はガウシアンカーブに従って0から増えていくそう。累積度数分布の関数みたいなかんじ…?
もう1つはTemporal Model。
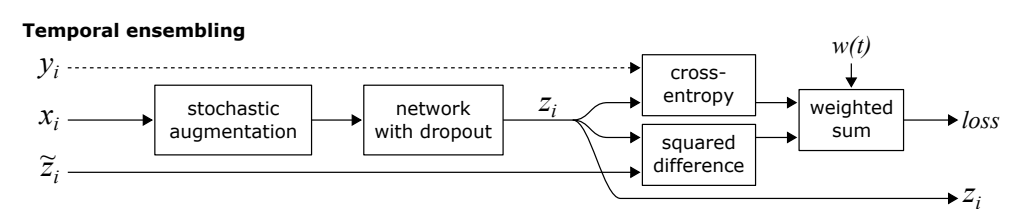
毎回のMini-batchでaugmentして学習するのではなく、毎回の学習のデータに過去ののものを割合減衰させる感じで学習データを混合させて、 のようにする。(の最初は0)そして、 としてノイズつきラベルとして扱って、上と同じように損失で評価する。
過去の学させたデータのラベルを一定数今のに混合させる感じ。まさにラベルアンサンブル。
論文: S. Laine and T. Aila, “Temporal ensembling for semi-supervised learning,” in ICLR, 2017. https://arxiv.org/abs/1610.02242 refer2725
他にも、各イテレーションを通して、Cleanなサンプルの集合を全体だとして集合から構築していく、ラベルアンサンブルベースの手法もある。self-ensemble label filtering (SELF) ってかっこいい名前。
- まず訓練用のデータで、Noisyなのを承知してモデル を訓練し、 とする。そして、アンサンブル用の蓄積させた と初期化しておく。
- 今の 検証用のデータで、現時点でのベストを上回る限り、以下のことを行う。
- ベストなモデルを更新。 とまず代入しておく。イテレーションカウンタを しておく。
- にあるサンプル とラベル について全部以下のことを行う。
- 学習器の予測結果 とする。( 次元のベクトルで各カテゴリの確率表す)
- アンサンブルしたラベルをハイパーパラメタ で指数減衰させる。 でラベルをアンサンブルさせる。
- さきほど更新したアンサンブルされた と与えられたラベル が異なる場合、これは間違っているということで、 から除外する。
- を で訓練する。
これによって、毎イテレーションごとに初期のNoisyなデータ集合からラベルが正しそうなもの選び出すことができ、これでさらに訓練を進めるというかたち。
基本的に、ラベルアンサンブルは慣性みたいなのを利用して、多少のノイズなら除外できるようなしくみ。
論文: D. T. Nguyen, C. K. Mummadi, T. P. N. Ngo, T. H. P. Nguyen, L. Beggel, and T. Brox, “Self: Learning to filter noisy labels with self-ensembling,” in ICLR, 2020. https://arxiv.org/abs/1910.01842 refer301
もう1つあるがよくわからなかった….
論文: X. Ma, Y. Wang, M. E. Houle, S. Zhou, S. M. Erfani, S.-T. Xia, S. Wijewickrema, and J. Bailey, “Dimensionality-driven learning with noisy labels,” in ICML, 2018. https://arxiv.org/abs/1806.02612 refer415
最適化のやり方
Early Stopを行うことなど、最適化のやり方次第でNoisyな部分を覚えさせないというのが可能である。
Memorization Effect
ArpitらがA closer look at memorization in deep networksにて、DNNは簡単な特徴=データの本質をまず覚えてから、次に複雑な特徴=ノイズを覚えるという学習傾向があるとわかった。つまり、Early Stopするべきということ。
これによって、small-loss trickという、「損失関数で小さい損失を持つ=Cleanなデータとして扱い、それらだけback propagationして学習を行う」という手法が開発された。上位 だけの割合をback propagtionする感じ。
Mentor Net
small-loss trickを実現するための手法。
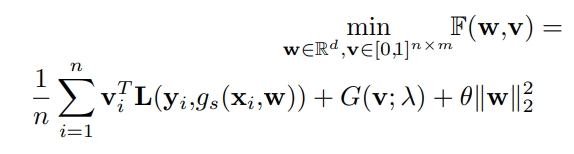
この式を最小化したい。 は各サンプルについての各損失ごとにLossに加算する重みのベクトル。 はstudent model のパラメタ。
一項目は各サンプルについての損失であり、二項目はカリキュラムとよばれていて、重みのベクトルについての学習の損失、最後のパラメタの重みの二乗和による正則化。
このカリキュラムについて、既存の手法では EMアルゴリズム?を使って の一歩を固定してた方を動かして最適化してきた。small-loss-trickでいうならば、小さい損失を持つロスのみ にして学習を進めるというやり方。カリキュラム項の はどれほど影響させるかを示し、モデルが未熟の時は小さいロスだけ、成熟してきたら大きなロスも取り込むようにするというような設計ができる。
手法1はすでに というsmall-lossの境界が定まっていて、 (見切れてる)があるときに機械的に以下のように決められる。上は既存のやり方で、下はカリキュラムを0 or 1ではなく、 の間に制限した有理数に広げたもの。以下の通り。
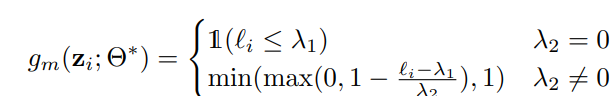
もう1つのやり方はDNNでデータ駆動で学習する手法。この手法では、MentorNetというDNNを用いて、本来の識別のDNNの重み を固定した時に、カリキュラムを訓練によって得る。(省略)
論文: L. Jiang, Z. Zhou, T. Leung, L.-J. Li, and L. Fei-Fei, “Mentornet: Learning data-driven curriculum for very deep neural networks on corrupted labels,” in ICML, 2018, pp. 2304–2313. https://proceedings.mlr.press/v80/jiang18c.html refer1527
Learning to Reweight
gradientの傾きに従って、異なる重みを各サンプルから寄与される損失に与える。弧の重みは動的に決定される。
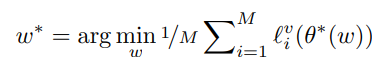
この式から重みは決定される、 は検証サンプルセットに置いての損失を取るという意味であり、 は識別器で は現時点での学習がされた最適の識別器。つまり、 カテゴリある中、検証サンプルセットにおいて、識別器の重みを固定した中で、それぞれのサンプルに対する重み を最適化するということ。
これを恐らく、 のように繰り返し訓練していく感じ。
論文: B. Han, Q. Yao, X. Yu, G. Niu, M. Xu, W. Hu, I. Tsang, and M. Sugiyama, “Co-teaching: Robust training of deep neural networks with extremely noisy labels,” in NeurIPS, 2018, pp. 8527–8537. https://arxiv.org/abs/1804.06872 refer1803
Co-training
Co-teachingという2つのDNNを訓練しながらお互い教え合う手法がある。ネットワークAとBがそれぞれ信頼できるサンプルを各ミニバッチから選び、Aが選んだのをBに与えてその損失をback propagationさせ、Bが選んだのをAに与えてその損失をback propagationさせる。
MentorNetでは1つのネットワークしかないので、重みの更新をして次はその重みでStudent Netが学習していた。これにより、一度誤った「信頼できるor not」の判定をしてしまったら、常に蓄積してしまう。Co-trainingは必ずしもすぐに蓄積されるわけではないので、よりロバスト性がある。
論文: X. Yu, B. Han, J. Yao, G. Niu, I. W. Tsang, and M. Sugiyama, “How does disagreement help generalization against label corruption?” in ICML, 2019 https://proceedings.mlr.press/v97/yu19b/yu19b.pdf refer694
Co-trainingのさらに先へ
3つほど研究がある。
Cross-Validationを利用して、信頼できるサンプルのサブセットを選び出す手法がある。
論文: P. Chen, B. Liao, G. Chen, and S. Zhang, “Understanding and utilizing deep neural networks trained with noisy labels,” in ICML, 2019. https://arxiv.org/abs/1905.05040 refer377
Co-teachingをするにあたって、small-loss trickを行うための閾値決定に、新しいニュートン法ベースのアルゴリズムを開発した。
論文: Q. Yao, H. Yang, B. Han, G. Niu, and J. T. Kwok, “Searching to exploit memorization effect in learning with noisy labels,” in ICML, 2020. https://proceedings.mlr.press/v119/yao20b/yao20b.pdf refer97
正則化項にエントロピーを加えることで、明確な分類を促すMixMatchから着想を受けた手法もある。
- 混合ガウス分布を用いて(どうやって…?)データを、信頼できるものとNoisyなUnlabeled2つに分ける。
- Co-trainingの亜種のアルゴリズムを使って、Unlabeledを明確にしていく。信頼できるものにはCo-refinementを、信頼できないものはCo-guessingを。そしてMixMatchを使てラベルの予測をばらけさせる。
Memorizationのその先へ
Memorization Effect以外を利用したDNNの特性の研究として2つある。
事前学習
事前学習によって、ロバスト性が上がるという研究がある。事前学習は大きなデータセットでまず訓練し、そこから小さいデータセットで学習することで、特化させる=fine tuning
Deep k-NN
まず、k-NNアルゴリズムを使ってNoisyだと思われるデータセットからきれいなものを選び出す。そこから、Cleanなと思うデータセットと合併して、目当てのモデルを訓練をする。
Future Work
データセットを増やす
Cloth1Mのデータセットはよく使われてきたが、ベンチマークとしてみんなこれにoverfittingしてしまうような傾向を示してしまう。新しいデータセットが必要。
また、実際の学習の目標として、音声認識というより画像認識でのNoisy Labelの門ぢ亜の方が盛んである。
インスタンスにも依存するノイズ方面の研究
今までは多くは を考えてきたが、インスタンスごとに異なり得る での研究をやるべきではないか。このままでは仮定があまりにも少なさすぎるので、いくつかの仮定を設けてのインスタンス依存のノイズの研究は進んでいる。いくつかの先行研究があって時間があると見ればいい。
Adversarialなロバストネスについて
今まではラベルが確かで、入力がnoisyな場合がAdversarial Exampleというのばかり考えられてきた。誤ったラベル付けと正しいラベル付けを識別する研究がある。friend-adversarial-exampleという研究もある。
Noisy LabelだけでなくNoisy Dataについても考えたい
特徴のNoise
Adversarial Exampleではまさにこれである。学習するときのサンプルごとの更新する度合いを変更することが有効な解決方法だと思われる。
Preference Noise
選択者の好みがrankingのアノテーションの中に入ってしまうので、それをうまく排除するような研究をしたいということ。
Domain Adaptationについて
ドメインごとのアノテーションの質が違うことで、Noisy Labelの問題に発展するよね= Wild Domain Adaptation。
Similarityベースの学習
AとBは近い、という情報だけを与えられて学習すること。ここでもNoiseの問題を考えることはできる。
Graph Neural Network
GNNは非常に研究対象としては良いが、これはNoiseにロバストなのか?
