Sen(Qian)’s Memo

https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=10264106&tag=1

先行のCost SensitiveのPU LearningはNegative AssumptionというPをNに多く判定してしまうバイアスを持っている。以下のように、Train Dataにおいて、Uの中でPと判別したデータの割合がClass Priorの$\pi$より小さくなるとわかる。ついでに、Test Dataについても過学習している。

解決法としては、訓練して得られたUの中のPの分布と、真のPの分布をAlignmentすることである(真のPの分布をどう得るのかはさておくとして)。だが、安易に導入すると、今度はUnderfittingとなってしまう。この研究はこれらの問題を克服した、PULDA(Positive Unlabeled Learning with Label Distribution Alignment)を導入した。

そのうえで、Objectiveに正則化項を加えてAlignmentすることは、確率的勾配降下法系で最適化すると収束しない問題がある。これについて、指数移動平均をベースにしたものを提案した。これは数学的に収束すると証明されている。

本論文の貢献は以下の通り。

• PULDAという新たな手法を開発した。
• 理論的証明や上界を提供した。
• PUにおける指数移動平均ベースの確率的勾配降下法を提案した。

この論文は 📄2022-CVPR-[Dist-PU] Positive-Unlabeled Learning from a Label Distribution Perspective の延長にある。

Class Priorがわかっている前提での手法として、以下のようなものがある。

• 📄2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data
• 📄2019-IJCAI-[PULD]Positive and Unlabeled Learning with Label Disambiguation
• 📄2017-NIPS-[nnPU] Positive-Unlabeled Learning with Non-Negative Risk Estimator
• 📄2019-ICML-[PUbN] Classification from Positive, Unlabeled and Biased Negative Data
• 📄2020-ICML-[Self-PU]Self Boosted and Calibrated Positive-Unlabeled Training
• G. Su, W. Chen, and M. Xu, “Positive-unlabeled learning from imbalanced data,” in Proc. Int. Joint Conf. Artif. Intell., 2021, pp. 2995–3001.

Class Priorが必要だが、選択バイアスがある場合の手法はいかのようなもの、

• 📄2019-ICLR-[PUSB]Learning from Positive and Unlabeled Data with a Selection Bias
• 📄2019-ECML PKDD-[PWE]Beyond the Selected Completely At Random Assumption for Learning from Positive and Unlabeled Data
• 📄2020-NIPS-[aPU]Learning from Positive and Unlabeled Data with Arbitrary Positive Shift

Class Priorの推定は以下の通り(全部はのせてない)

• 📄2020-AAAICAI-Class Prior Estimation with Biased Positives and Unlabeled Examples
• 📄2016-NIPS-Estimating The Class Prior And Posterior from Noisy Positives And Unlabeled Data
• 📄2021-NIPS-[TEDn]Mixture Proportion Estimation and PU Learning: A Modern Approach

Class Priorがそもそもいらない手法

• M. Hou, B. Chaib-Draa, C. Li, and Q. Zhao, “Generative adversarial positive-unlabeled learning,” in Proc. Int. Joint Conf. Artif. Intell., 2018, pp. 2255–2261.
• 🚫 Post not found

• データは$\mathbf{x} \in X \subseteq \mathbb{R}^d$である。
• Ground Truthのラベルは$Y = \{ 0, 1 \}$であり、1がPで0がN。
• シナリオはCase Control(2 Sets)。Uデータは$X_U \sim p(\mathbf{x})$でサンプリングされる。

PN Learningにおいて、誤分類の確率は以下のように分類できる。

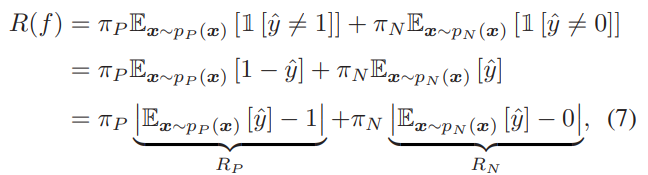
これを代替損失を使って識別器自体を訓練するとき、このように絶対値で予測分布と真のラベル分布のAlignmentはおのずとできる。

PU Learningにおいて、同様に展開する。UはClass Prior$\pi_P$の割合のPと$1 - \pi_P$の割合のNによって構成されているという前提。PN Learningのように考えると、Uの中のPの割合は$\pi_P$より多くてもすくなくても望ましくない。($R_P$は上の式を代入)

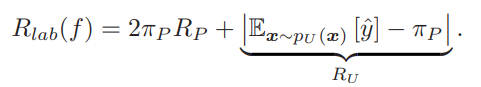
もう1つの考えとしては、以上のものとはまた少し違う。

先ほどの式を導いた$\pi_N R_N = \mathbb{E}_U[l(g(\mathbf{x}), y)] - \pi_P + \pi_P R_P$についても、この値は負になってはいけないということから、以下のようなものである。

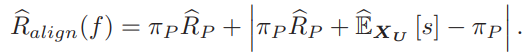
これはより厳しい整合条件だといえる。

📄2022-CVPR-[Dist-PU] Positive-Unlabeled Learning from a Label Distribution Perspective では、普通に先ほどのAlignmentを行うだけなら、Uの予測結果は$\pi_P$の近くに集まっていて、結果として予測できない、もっと0か1かにばらけてほしい($R_{lab}, R_{align}$を使うといずれもそうなりそう)。それを防ぐため、新たなObjectiveを提案した。

Dist-PUではBinary Cross Entropyを導入していた。この論文では、ある信頼下限$\rho$を導入し、たとえ分類に成功しても$\rho$以下の信頼度だったら学習器にペナルティを与えるというもの。

$f(\mathbf{x})$の正負で判断するということをもとにさらに式変換すると、

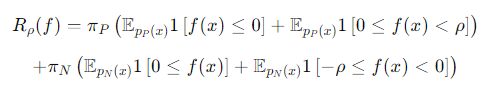
「0より大きいか小さいか」の部分はPかN判断へのペナルティ。「$\rho$の範囲にに収まるかどうか」は信頼度のペナルティ。

あとは、これはPNの式なので、同様にPUの式に直す。$\mathbb{E}_N[\mathbf{1}[0 \leq f(\mathbf{x})]]$は判断へのペナルティで、既存のuPUやnnPUですでに書き換えができている。信頼下限の$\rho$については、以下のように買い換えられる。

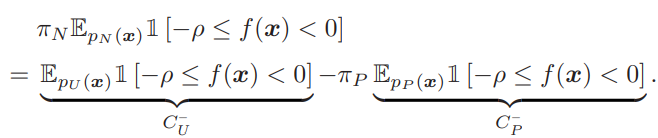
したがって、全体の式は以下のようになる。

具体的に、指示関数のままではできないので、以下のようにSigmoid関数で指示関数$\mathbf{1}[0 \leq f(\mathbf{x}) \leq \rho]$らを書き換える。

一項目の$\{ 2\pi_P \mathbb{E}_P[l(f(\mathbf{x}), +1)] + \mathbb{E}_U[l(f(\mathbf{x}), -1)] - \pi_P \}$については、後者は$R_U$に相当する損失である(DistPUでも同様)。

だが、以下の条件を満たすような関数$g$に代入して、過小か過大予測しないようにするらしい。

• 連続で、負から0は単調減少、0から正は単調増加。
• 有限の入力に対しては有限な出力をする。

具体例としては、以下のようなSoftPlus関数を組み合わせたものを$g$としている。

これを、本来の$R_U$のみならず、マージンについてのペナルティのU部分にも適用させる。

結果として、以下のような式を得て、これが今回のObjective。図らずしも$R_{lab}$の改善版のような式になっていた。

DistPUではEntropy最小化で実現していたが、ここではマージン最小化+U項への補正で実現している。

このままの確率的勾配降下法による最適化するとき、$g$という関数を本来のUについての項を噛ませているが、以下のように実は期待値では成り立たないという悲劇がある。

これを改善するために、指数移動平均を用いる。

$g(\cdot)$にあたえる要素は$r_i(\mathbf{w})$ではなく、今までの$r_i(\mathbf{w})$の移動平均とする。

移動平均自体は以下のように計算する。