Sen(Qian)’s Memo

https://nips.cc/virtual/2023/poster/71501

先行研究はこちら

📄2017-AAAIAI-Robust Loss Functions under Label Noise for Deep Neural Networks.

📄2020-ICML-[APL]Normalized Loss Functions for Deep Learning with Noisy Labels

クラス$k$に対して、与えられる正解の分布は$q(k|x)$であり、識別器の予測分布は$f(x) \to p(k|x)$である。

いろんな損失関数をNoisy Labelの場合で試して検証してみた。

また、損失関数を以下のようにNormalizeするとNoisy Labelに強くなる。すべてのクラスについての損失の和が1になるように正規化する。

理由としては、不明。極端な値をとる場合はほかの項も極端な値をとっているので、結果的に釣り合う？

ただ、これではUnderfittingの問題があるという。例えば、

損失関数にはActiveとPassiveがある。

• Active　$Pr(y|\mathbf{x})$(所属するクラスの確率)を最大化する。
  • 例えば、Cross Entropy、Focal Loss、Normalized CE/FL
  • 具体的に言うと、正解クラス$y$以外のクラス$k$が正解だったら、と擬して損失を考えないつまり$l(f(x),k)=0$。
    • 実際Cross Entropy損失では以下のようになる。ラベルはone-hotならば、$q(y|x)=1, q(k|x)=0$であるので、以下のようになる。
    $l(f(x),k)= -q(k|x) \log p(k|x) \\ L(f(x),y)=- \sum_{k=1}^K l(f(x),k) \\ \forall k, k \neq y, q(k|x)=0$
• Passive　$Pr(k \neq y | \mathbf{x})$をすべての$k$について最小化する。
  • 例えば、MAE, Reverse Cross Entropy, Normalized MAE/RCE
  • 具体的に言うと、正解クラス$y$以外のクラス$k$についても、と擬して損失を考えるつまり$l(f(x),k)\neq0$。
    • MAEは以下のようになる。
    $l(f(x),k) = |p(k|x) - q(k|x)|^2 \\ \exist k, k \neq y, |p(k|x) - q(k|x)| \neq 0$

先行研究で提案したように、Active LossとPassive Lossを組み合わせたもの。これにより、Underfittingが抑制されるらしい。謎…?

MAE, RCE, NMAE, NRCEの4種類があるが、RCEも以下のように、与えられるのはHard Label出ることから、MAEになる。

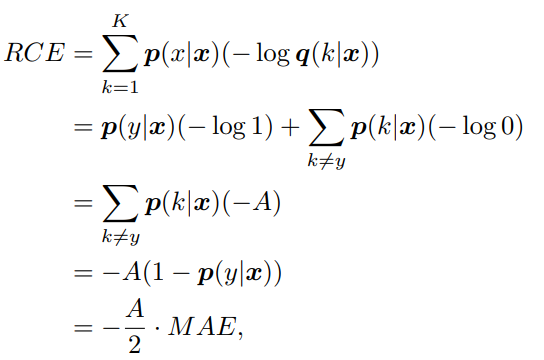
なので、新しいPassive Loss Functionの開発を考えたい。

既存の手法では達成できないようなMinimizingができる、Passive Lossである、Noisy Labelに強いの3要件を兼ね備えたものにしたい。それぞれ

• 達成できないような最小化=Complementary Label Learning
  • 正解のラベル以外が与えられる感じ。
• Passive Loss=垂直フリップ
  • 単純に以下のようにある定数$A$を使って、最適化を最大化から最小化にしていること。

  

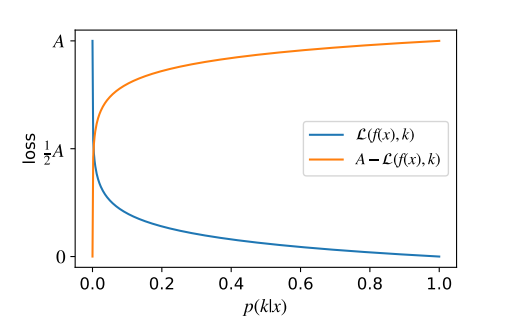
  • Passive Lossの具体例として、Hard Labelに対するCross Entropy Lossは$L_{CE}(f(x),y)=-\log p(y|x)$である。これに対して、$A - L_{CE}(f(x),y)=A + \log p(y|x)$を考える。
    • $p(y|x)$が大きくなると、元の損失関数は小さくなるが、符号をひっくり返したVertical Flippedした損失は大きくなる。
    • 損失関数を最小化したい、という大枠の目的は変わらないので、「もともとの損失での$p(y|x)$の最大化」を「Flipした損失での$p(y|x)$の最小化」にすることができる。これ自体がPassive Lossの非該当クラスの要件を満たす。
• Noisy Labelに強い=正規化　これは 📄2020-ICML-[APL]Normalized Loss Functions for Deep Learning with Noisy Labels にあるように。

で実現している。

これらを踏まえてまず、Negative Loss Functionを提案する。

Vertical Flipを使うことで、任意のPositiveの関数を$\forall k, k \neq y, p(k|x)$の最小化の目的関数にできるので、できるだけクラス$k$に合致しないようにするため$A - L(f(\mathbf{x}),k)$を最小化するNegative Loss Functionを考える。

各クラス$k$については、より与えられたラベルの中であり得ないようなクラスほど(つまり$1-q(k|\mathbf{x})$が重み)、合致しないようにするNegative Loss Functionの項を重くする。これによって、あり得ない度が高いほど、うまく$A-L(f(\mathbf{x}),k)$を最小化していくインセンティブが生まれる。

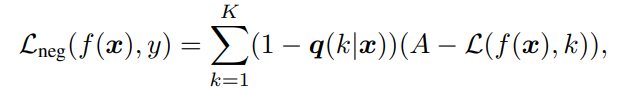
この時、$\log 0=\infty$になるみたいなことが起きるので、最も低い予測確率でも$1 \times 10^{-7}$としている。うまいこと上限をcaptionする必要がある！

あとはこれを正規化すればよい。クロスエントロピー損失である場合の実例も示す。

これもActive Passive Lossに倣い、Active Negative Lossというのを考える。Negativeは補ラベルを使って考えたから。

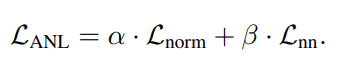
前は正規化されたActive Loss。後ろは正規化されたNegative Loss(補ラベルベースの)。

このように考えた正規化されたNegative Lossも、対称である。以下の証明では、全クラスに対しての損失の和を加算したっけか定数となるので、これは対称的な損失であると示せた。

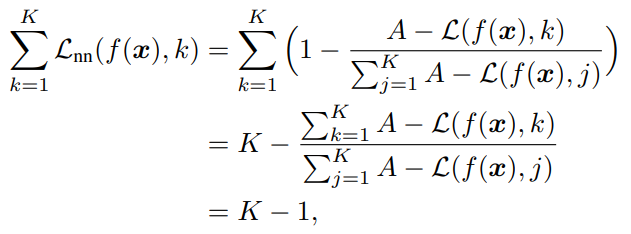
そして対称的な損失は、Noisy Labelに強い。

デフォルトの唯一のPassive LossだったMAEでは、微分した際は以下のようになる。

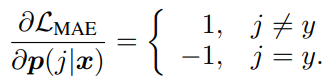
正規化されたNegative Lossの一例である、Cross Entropy LossのGradientは以下のようになる。

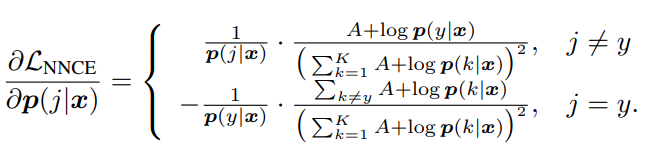
定数であったMAEと違い、こちらでは

1. $a\neq b \neq y, p(a|x) < p(b|x) \Rightarrow$$a$時点の勾配は$b$時点の勾配より大きい。
   1. 正解から遠い=確率が低いほど、Gradientが大きくなる。
2. 同じクラス$y$に属する2つのサンプル$x_1, x_2$に対して、ある別のクラス$j$については$p(j|x_1)=p(j|x_2)$であり、それ以外では
   1. $p(y|x_1) > p(y|x_2)$。つまり、$x_1$のほうが確信度が高い。
   2. $p(k|x_1)<p(k|x_2)$。つまり、正解の$y$や等しい$j$以外ではやはり$x_1$のほうが誤った判断をしていない。

   これらの条件を満たすとき、$x_1$のGradientは$x_2$より大きい。

   他と比べて正解に近く、所属してはいけないクラスの確率自体も低いほどGradientが大きくなり、正直うれしくないかも。

Loss Function Correctionだけなのに、Small Loss Trickなどと比べて高いノイズ率でもちゃんと学習できている。普通はLoss Function Correctionは高いノイズ率には無力なので、これは非常にびっくり。

過学習については、正規化したNegative Loss Functionが原因で、非常に少数のCleanなサンプルだけで学習をするモデルの場合、非常に大きい勾配が生じてその結果過学習するという考察。

過学習の軽減にはL1正則化が有効。L2やヤコビアンの正則化は不適当である。