2022-NIPS-Positive-Unlabeled Learning using Random Forests via Recursive Greedy Risk Minimization

https://arxiv.org/abs/2210.08461

Introduction

現在のPIU Learningの主流は基本的にDNNの識別器を用いる。決定木ベースの手法についてのPU Learningの先行研究はほぼない。決定木ベースの方法についてのRisk Estimatorもないのが現状である。

これに対して、再帰的な貪欲リスク最小化という方法を考えた。主な貢献は以下の通り。

新たな決定木のPU Learningのアルゴリズムを開発した。
様々な損失関数を変えても、同じ決定木が導出されるロバスト性がある。
DNNベースの手法と比べて、ハイパラの調整がほとんど不要。

Background

PNデータを用いた決定木の学習

決定木とは以下のようなアルゴリズムである。

ノードについて、割り当てられているデータの集合 $S$ について、終了条件を満たしているなら、そこで終わり。
1. 今のノードにたどり着いたら予測結果は○○と決めておく。
満たしていないないのならば、特徴量と閾値に基づいて最適な分割を計算し、 $S$ を $S_1, S_2$ に分けて、それぞれ子に渡して再帰的に計算させる。
1. ここでいう特徴量は、データのある次元についてBinary Cross Entropyやジニ係数を指針に、今のBinary Cross Entropyの値やジニ係数の値をどう分ければ最小になるかを考える。

再帰的な貪欲リスク最小化

まず、各データはPかUであるが、それぞれに対して重み $W$ というものが存在する。

PNデータについての決定木

PNデータについて決定木を行うとき、 $R(g) = \mathbb{E}[l(g(\mathbf{x}), y)]$ について同様に、分割前と分割後で減少するのを最大化したい。

これはジニ係数やBinary Cross Entropyとは違うアプローチのように見えるが、以下のように実は同じようなフレームワークに落とし込めている。

二乗損失を使った分類はジニ係数の定数倍。
シグモイド損失を使った分類はBinary Cross Entropyの定数倍。

なおここでは、損失関数 $l$ を定義する必要があるが、このままではどうも $l$ 次第で決定木の構成がかなり変わりうるらしい。

PUデータについての決定木

uPU

📄2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data

PUデータを決定木で分けるとき、どのような指標の関数で分けるべきか？uPUの指標関数で分けると考える。

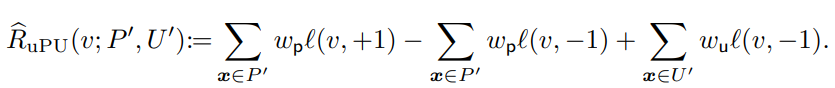
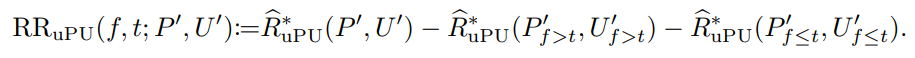
損失に具体的に二乗損失やシグモイド損失を代入したのが以下の形。

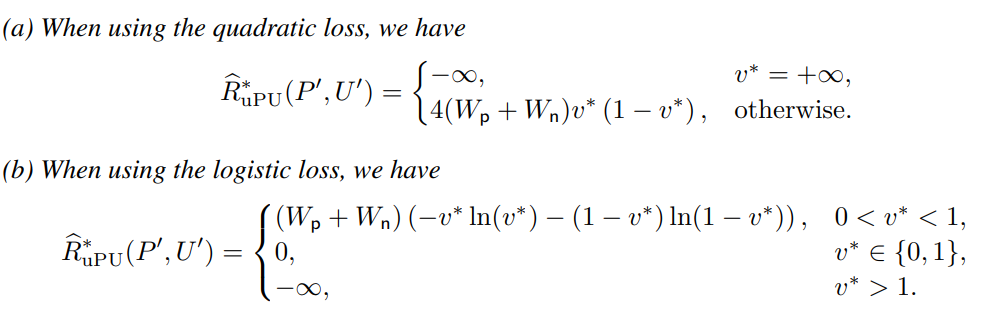
分割したとき、uPUは損失を保存する。

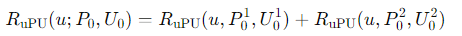
nnPU

📄2017-NIPS-[nnPU] Positive-Unlabeled Learning with Non-Negative Risk Estimator

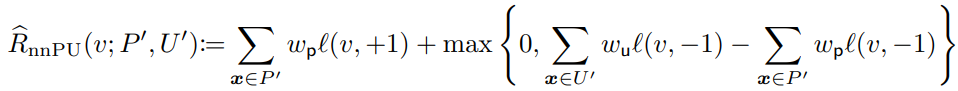
分割したとき、nnPUは損失を保存しない。

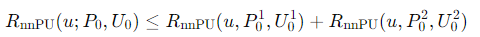
なので、nnPUにおいての最小化は実は損失の最小化ではなく、上界の最小化。

二乗損失は極端に違う予測値のペナルティを大きくする。
$v^* = W_P / (W_P + W_N)$ とする。これは、Pのデータの占める重みの割合である。
$W_P \in [0, 1]$ と制限しているが、 $W_N$ は負の値をとりうる。
$W_P + W_N = 0$ の場合、 $v^*$ は無限大になる。

計算上の実装

分割は $(f, t)$ で定義されており、特徴量 $f$ を、閾値 $t$ より大きいか違うかで分割する。

各特徴量について、それぞれ閾値は理論上連続なので無限に存在するが、当然データの個数ぶんしか試さなくてよい。 $f$ の取る値は高々 $|P_{node}| + |U_{node}|$ 個なので、以下のように $|P_{node}| + |U_{node}| + 1$ 個だけ探索すればよい(それはそうだ)

$f$ の取る値をソートする。
前後に $-\infty, +\infty$ をつけて番兵とする。
お互い隣り合う要素の平均をとる。
3で得たものを閾値とする。

PU Extra Trees

決定木について議論したので、Random Forestも考えられる。

PU ET(Extra Trees)

Extra Treesアルゴリズムとは

Pierre Geurts, Damien Ernst, and Louis Wehenkel. Extremely randomized trees. Machine learning, 63(1):3–42, 2006.

Random Forestの変種でさらにRandom性をあげたもの。通常Random Forestでは、「特徴量」、「使用するデータ」が各決定木ごとにランダムであるが、Extra Treesでは「特徴量についての閾値」もランダムに選ぶ。(これにより閾値決定の計算は不要になる)

ということで、流れとしては今の決定木で使用する候補の特徴量すべてについて、ランダムで選んだ閾値をもとに計算する。その中で最善のパフォーマンスを出したものを選ぶ。

ここまでランダムにしても、数を重ねれば収束できるのである。

終了条件は

すべての特徴量が同じになった場合。
最大の深さに到達した場合。
ノード内のデータが少なすぎた場合。

これをそのままuPU, nnPUの損失に適用させる。

終端ノードについて

含まれているノードのうちのラベルが多い方が予測結果(それはそうだ)。

普通は完ぺきに分類できるまでやるが、過学習を引き起こすのでたとえ完璧に分類できなくても、最大の木の深さ $d_{max}$ を超えたらそこで打ち止めにする。

Experiments

Datasetは以下のようなものである。
- 20News: Pはalt, comp, misc, rec。Nはsci, soc, talk。
- MNIST: Pは0, 2, 4, 6, 8。Nは1, 3, 5, 7, 9。
- CIFAR-10: Pは0, 1, 8, 9。Nは2, 3, 4, 5, 6, 7。
- UNSW-NB15: すべてのAttackがPであり、正常データがN。
- mushroom, covtype: 最も頻繁に現れるP、それ以外がN。
- epsilon: そもそも二値分類データセットである。
モデルは以下のようにする。
- 100本の決定木でのRandom Forestである。
- 最大の深さに制限はなし。
- 全体の特徴量 $d$ 個から $\sqrt{d}$ 個を毎回選ぶ。
- 最適な分割をするときに1つの閾値を選ぶ。
損失関数は、Binary Cross Entropyのほうがよさそう
Random Forestでも、DNNベースの手法に勝ることはあるぞ！