論文: https://arxiv.org/abs/2006.04662
Introduction
Distribution Shiftがあるデータで学習するのは簡単ではない。同時分布が違うというのが一番広い仮定。何も対処しなければ、大きく性能を落とすことがわかっている。
一般的な手法として、以下のように密度比を推定するというものがある。この手法は、Importance Weightingという。
まずは密度比を推定し、その後Train Dataに密度比を乗じたものをTarget Domainのサンプルだとみなして学習をしていく。
しかし、密度比推定は複雑なデータ、そして表現力が高い学習器=DNNなどでは性能が大きく下がる。識別器が次元の入力を受け取るDNNな時、密度比を推定するならクラスも合わせた次元くらいは必要で、既存手法だと表現力が足りない
この論文では、DNNを使った密度比推定はなぜうまくいかないのかを3つの理由で説明している。
- 密度比推定の手法はモデルフリーである。
- モデルベースの手法は存在していても、以下の条件の制約の式の元で解いているので、確率的な解法には向いていない。
- じゃあ密度比推定をDNNにやらせればいいのかというとそうでもない。各ミニバッチ内で制約を無視したとしても、DNNは密度比推定には向いていない。
なので、を推定するには、もっと次元を落とした入力が必要で、そのためには特徴抽出器が必要なのだが、それってまさに訓練したいだよね。つまり循環依存に陥っている。
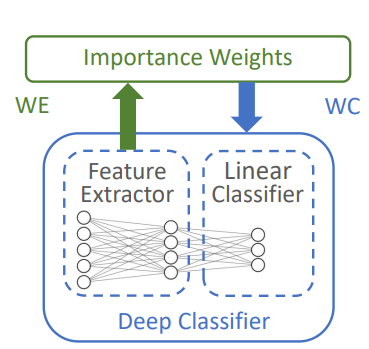
この循環依存を解消する2つの案を提案した。
Pipelined
事前に訓練した、重みなしデータでのDNNによる学習器を用意する。この学習器から特徴抽出器を用意する。このとき、密度比推定をしたとして、それから本命の識別器を作る。この時、特徴抽出器をもう一度学習しないので、重みは変わらずStatic Importance Weightingとなる。
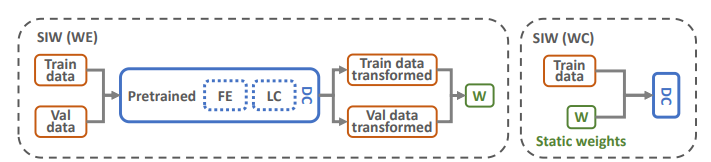
右がオリジナルで、左が提案したPipelined。残念ながら重みが決まっているので、ほんの少ししか性能が上がらない。
では、重みを動的にすればいいじゃないか=Dynamic Importance Weighting。
Co-training, 📄2018-NIPS-Co-teaching: Robust Training of Deep Neural Networks with Extremely Noisy Labels 、📄
2018-ICML-MentorNet: Learning Data-Driven Curriculum for Very Deep Neural Networks on Corrupted Labels などにもあるように、毎イテレーション両方更新し合うことで、動的に変化させればいいよね。
これを実現する手法を提案した。
Dynamic Importance Weighting
問題設定
手元にあるのは、のSource Domainの訓練データと、Target Domainのの検証データである。
以下のように、訓練データのSource Domainから学習をするには、適切に学習された重みWeight Estimatorを用いて、経験的に算出される損失で学習をする。
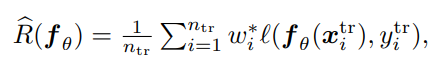
データの非線形変換
表現力をあげるため、密度比推定やの推定自体をDNNでやるべきではない。つまり、外部の特徴抽出器でうまい特徴を抽出して、密度比推定自体は線形のままで行うのが望ましいということ。
理由としては、論文ではWeight Estimatorの表現力を高めるのは内部的には困難である(たぶん実験的事実)
特徴抽出器で、もともとの次元よりもさらに低い次元に落とすべき、ということ。として、特徴抽出器を使う。
実際に、以下のように密度比推定では、双方を特徴抽出器に入れたあとのの密度比にしていい。ただし、以下の3つの条件を満たす必要がある。
- 決定的である は同じ入力には常に同じ出力がある。
- 固定されている 訓練中では不変。
- 可逆である 特徴抽出器から得た特徴で、復元できる。
- まあ、現実的には無理であると後々言われるが…
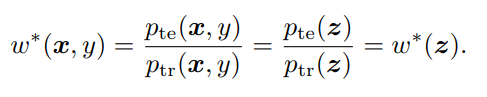
証明としては、以下のように密度比の積分で書き換えられるから。は累積密度関数。
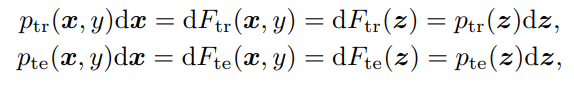
が固定されていないと、は必ずしも成り立たない。が決定的ではない、可逆ではないならは必ずしも成り立たない。
これらを踏まえて、実際にWeight Estimatorを訓練する上では特徴量が必要なのだが、その特徴量を得るためにはWeight Estimatorをもとに訓練した識別器を使うのが一番である。そういう矛盾がある。
の選択
一般的に特徴抽出器は、識別器の隠れ層の値を使えばいい。
Hidden-Layer-Output Transformation Version
共変量シフト、の時に、以下のようなことが成り立つ。
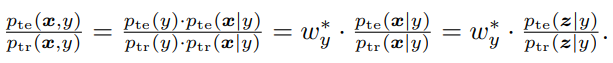
このように推測することで、まずはを、次に各クラスに所属してるサンプルの分布などがわかるので、これで経験的に推測する。しかし、明らかにただでさえミニバッチ学習をする中でさらにクラスに細分して推定をするのは明らかに、著しく信頼性を損なう。
Loss-Value Transformation Version
なので、この論文では代替案として、直接予測した値を推定し、そこに損失関数を計算するのではなく、損失関数を経過させた後の値を推定する。
この時、上の3つの条件のうち、可逆性は崩れる。また、上の密度比の書き換えの式でも成り立たない。だが実用上役に立つ。
この手法では、以下の条件を満たす重みを探す。つまり、損失関数適用後に密度比を乗じているのである。
これの推定は、毎イテレーション?エポックごとに行うので、動的なImporance Weightingとなる。
アルゴリズムの全体像
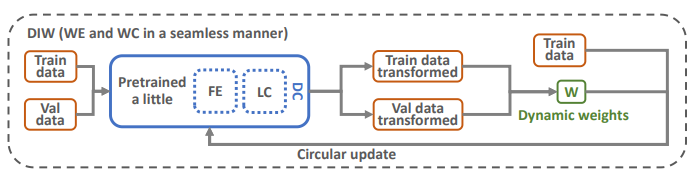
以上の流れを解説していく。
- 事前学習で特徴抽出器を作り、そこから線形でTrain, Test両方の特徴をFeature Mappingする。
- そこから、損失関数計算後の密度比を今の特徴抽出器に基づいて、計算したサンプルの特徴に基づいて、重みを動的に決める。
- 最後にbackwardして、特徴抽出器の学習に反映する。
具体的な分布のマッチング
密度比の推定自体は伝統的な高次元の再生核ヒルベルト空間に写像して、そのうえでMax Mean Discrepancyを測定して最小化する。
具体的には、📄2021-Survey-A Comprehensive Survey on Transfer Learning (Part1) Instance Weighting Strategy を参照。
具体的には目的関数を変形して以下のものの最適化に帰着した。
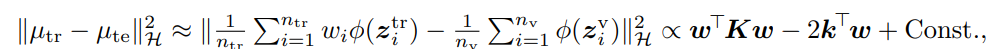
Hidden-layer-output transformation version
Hiddenのほうのアルゴリズムは以下の通りである。
ミニバッチ内でクラスごとに分割したあと、クラス別の条件付分布による密度比の推定である。
その後損失を計算し、識別機本体をbackwardして更新する(この時特徴抽出器は隠れ層なので、一緒に更新される)

Loss-Value Transformation Version

損失まで一気に計算させた後、Lossの密度比を推定する。そして、backwardする。
ここでは、隠れ層が介在しない。
毎イテレーションMatchingさせているが、本来は学習をする前にすべてのデータをMatchingさせて密度比を計算している。しかし、今回は損失のMatchingであり、学習しながら損失は変動していくので、各Minibatchでその都度その都度Matchさせて、学習を進めている。
Applications
共変量シフトは以下の通り。
一番簡単そうなのは、Class-prior Shiftである。
これの時はとりわけ簡単で、密度比を計算すればいい。
一番難しい、敵対的な設定はLabel Noiseである。共変量シフトの逆といえる。
Discussions
Domain Shift関連で以下の関連話題がある。
Learning to Reweight
訓練データについては重み付き分類で識別器を学習し、検証データについては重みなし分類で密度比を学習する。
例として、Train Dataのラベルの偏りを是正するために、各サンプルに重みをつけている。
Importance Weightingと似ているように思えるが、IWは最適な重みを推定するのが目標だが、Learning to Reweightに目標はない(しいて言うなら全体の識別器の性能向上)
技術的には、更新する重みが学習器のパラメタの一部であるわけで、密度比推定は別物だと考えている。これはIWよりも難しいタスク。
Distributionally Robust Supervised Learning(DRSL)
検証データは得られない上、最悪を招く敵対的な摂動を考える。
IWでは、testが固定されているうえで、trainをシフトしている。しかし、DRSLはtrainを固定して、testをシフトさせてhackケースを作っている。
Domain Adaptation
教師ありのDAはこの手法と似ているが、教師なしのほうが最近研究のトレンドである。
Unsupervised DAでは、が不変であるという仮定が多いが、IWはこれが変わる=Label NoiseになるのでUnsupervised DAのアルゴリズムでは対処できない。
Experiments
FMNIST,CIFAR10,CIFAR100を使う。
FMNISTのbackbornはLeNet-5。CIFARのbackbornはResNet32。
そして問題設定としては、Label NoiseやClass Prior Shiftの両方で使われた。
- 1000個のランダムなクリーンなデータをLabel Noiseの実験に使う。
- 1クラスあたり10個のランダムのデータをclass prior shiftの実験に使う。
