https://proceedings.neurips.cc/paper/2020/hash/1e6e25d952a0d639b676ee20d0519ee2-Abstract.html
Introduction
最適輸送はDivergenceにかわる分布の近さの指標の1つである。尺度となる距離は、Monge-Kantorocivh距離かWassertein距離を使ってきた。
現在のWassertein距離を使う場合では、分布gあ同じ基底空間に属している最低でも違うドメイン間でも有意に距離を計算できるのが重要。
つまり、2つのドメインの最適輸送の計算には基本的に対応しづらい。
しかし、現実はそうでもないことが多い。Gromov-Wasserstein(GW)距離の導入によって解決できるようになったらしいが、それでも計算負荷が重い。現在の主流は、Entropy正則化やSinkhornの反復による解法である。
この論文は初めて最適輸送をPUに導入してみた。
最適輸送について
最適輸送について以下にまとめている。
部分的なWasserstein, Gromov-W距離
部分的なWassertein距離
最適輸送といったが、全部運ばなくていい。これも📄最適輸送について にある。
Optimal Transport一般の手法の1つとして、部分的輸送を実現するにはDummy Pointを作って、そこにいらない量、超えてしまう量を割り当てさせる、というテクである。これを使うことで、一般的な最適輸送と同じように解くことができる。
双方にダミーのデータ点を追加して、コスト行列に新たに拡張を加える。
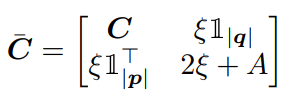
として、絶対的に大きい値をとる。はある程度大きな値で、ダミー点利用をある程度抑えるためのもの。これによって、ダミー点から、タミー点への輸送にはそれぞれペナルティがかかる。
それを承知でも、ダミー点を使うということで部分的な最適輸送が成り立つ。
部分的なGromov-Wasserstein距離
同様に部分的な最適輸送について、Gromov-Wasserstein距離でも考えてみたい。
同様にDummy Pointを追加したいが、GW距離では各Domain間のペアごとの距離の計算を行うが、各Domainの内部構造の計算をする以上、Dummy Pointが入ると内部構造の計算が崩れてしまいより計算が逆に難しくなるので、できない。
代わりに、Frank-Wolfe Algorithmによって実現する。アルゴリズムは略。
Method
UをSource Domain()、PをTarget Domain()のデータとみなす。
そして、部分的な輸送では、と、Source Domainの中からちょうどPのぶんだけTarget Domainに輸送したい。
具体的には、以下のような設定で最適輸送を解いた。
- 各データごとの重みは。
- 部分的最適輸送を解く。
- の条件では、厳密にと等しいという条件設定。(ちゃんとUから運び出すの量は、Uのうちのから計算されたPの割合と等しくないといけない)
- 逆に、UからP運び込まれる量は、Pに元々ある量と関係は特にない。
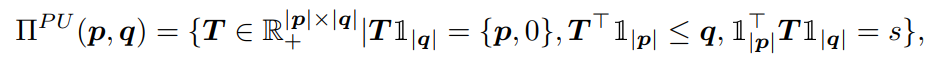
そして、Pの中でもノイズが混入された可能性があるとして、Pの中での割合のデータが間違っているというのを考える。
この時、以下のような最適輸送計画を立てることができる。
- で、である。
- ノイズが多いほど、輸送量を減らす。なぜなら、そもそもPが信頼できない以上無理に運ぶ必要がないと考えているからだ。
- A
- という正則化項も付け加える。ここでは、以下のようになる。輸送量が1つのルートに偏りすぎないようにする!
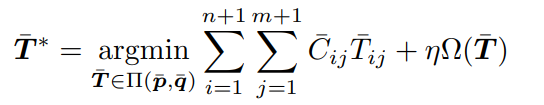
Experiments
のWassertein距離を使い、コスト行列自体はユークリッド距離を用いた。
SAR仮定での実験はMNISTとColored-MNISTで実験した。
Domain Shiftをちゃんと考慮する必要があるときはGWの性能のほうがやはり良い。Caltech Officeのデータセットでテストした。いずれもPCAなどで次元削減した特徴でPUしたらしい。
輸送行列の要素に0が多くなるような疎行列となる解を得るには、正則化項の重みを減らす必要があるが、こうすると最適輸送の収束までの計算コストが上がってしまう。
