https://arxiv.org/pdf/2006.13554
Introduction
今のNoisy Labelに対する戦略は以下の4つがある。
- 誤ったラベルを見つけ出し、訓練に使わない。
- ノイズの生成モデルを考える。行列などで。
- 訓練するときのアルゴリズムを改善して、ノイズを考慮させる。
- そもそもノイズに強い損失関数を作る。
- 今回の研究はこれ
- 先行研究としては、 Generalized Cross Entropyがある。
- Reverse Cross EntropyとCross Entropyを組み合わせた、Symmetric Cross Entropy損失もあるらしい。
- Wang, Y., Ma, X., Chen, Z., Luo, Y., Yi, J., and Bailey, J. Symmetric cross entropy for robust learning with noisy labels. In ICCV, pp. 322–330, 2019c.
📄2017-AAAIAI-Robust Loss Functions under Label Noise for Deep Neural Networks. であるように、絶対値損失のMAEは損失に強いが、クロスエントロピー損失が弱いのは残念である。だが訓練の収束速度では圧倒的にCross Entropyが早い。
MAEとGeneralized Cross Entropy(読んでここにリンク張る)ではこの欠点を補おうとして、MAEとCross Entropyを組み合わせたといえる。しかし、これは理論的には部分的にしかノイズに強くないらしい。
この論文では、理論的にどのような損失関数からでも、正規化をするだけっでノイズに強いような損失関数を構築することができる、と示した。
しかし実際では、単にRobustな関数は、そもそもピークの性能が低い学習不足の問題をDNNでは抱えている。なので、あらたにActive Passive Lossという概念を考えた。
Related Works
前述の通り4つの戦略がある。具体的にはだいたい 📄2020-Survey-A Survey of Label-noise Representation Learning: Past, Present and Future にある通り。
提案手法
問題設定
- データはで、ラベルはである。
- ラベルはという分布として与えられるとする。最も分布はonehotである。
- 真のラベルはであり、Noisyされた後のラベルはとする。
- 識別器はラベル分布の予測を出力し、だとする。
- ノイズはインスタンスに依存しない。
- つまり、典型的な対称、非対称損失を考える。
よく使われる各種の損失関数
- Cross Entropy(CE)
- Mean Absolute Error(MAE)
- Reverse Cross Entropy(RCE)
- Focal Loss(FL)
提案手法: 正則化
📄2017-AAAIAI-Robust Loss Functions under Label Noise for Deep Neural Networks. で提案されたように、以下のような対称的な損失はロバストであるとわかる。
これを実現するには、以下のように損失を正規化すればいいとわかる。
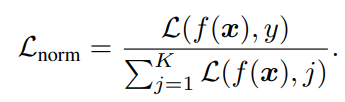
先ほどの提案した4つの損失について、それぞれNormalizationを考えてみた。
- Normalized Cross Entropy

- Normalized Mean Absolute Error
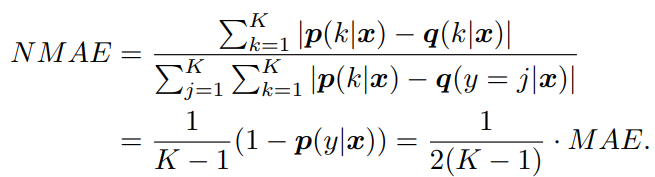
- Normalized Reverse Cross Entropy

- Normalized Focal Loss
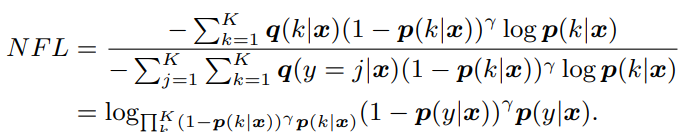
NMAEとNRCEは、元の損失の値から定数倍で変換できるとわかる。
理論的な部分
📄2017-AAAIAI-Robust Loss Functions under Label Noise for Deep Neural Networks. にもあるように、以下のが成り立つ。
- 先行研究のように、ノイズ率ならば、正規化された損失関数も対称非対称損失の両方に強い。
- 正解ラベルはたとえノイズがあってもさすがに多数でないといけない。
- 先行研究のように、として、を満たすときは対称、非対称損失の両方に強い。
- 正解ラベルはたとえノイズがあってもさすがに多数でないといけない。
- ここでとは間違っているクラスは(正規化された)損失を高く持つべきであるが、それでも各クラスごとの平均のを超えてはならない、という意味。
- 間違ったクラスであっても損失が過度に高くないことで、ラベルは実は間違っていました、となっても被害を軽減するしくみ。
Robustness Alone is not Sufficient
ここまで正規化によって高いロバスト性を持つことができると示したが、実用上ロバスト性が高いだけではまだ不十分である。ロバスト性が高いと、そもそも学習が進まずにピークの性能が低い学習不足を引き起こすことが実践するうえで分かった。
これに対してこの論文はActive Passive Lossというフレームワークを提案した。
Active Passive Loss
すべての既存のロバストな損失関数は以下のように分けられる。
- Active Loss 該当するラベルである確率をより高めようとするような損失関数。
- つまり、に近づけようとする。
- CE, NCE, FL, NFL
- Passive Loss 「Active Lossの役割に加えて」該当しないラベルである確率もより低くしようとするような損失関数。
- MAE, NMAE, RCE, NRCE
ということで、ハイパーパラメタを取り入れることで、Active Passive Lossを以下のように定義できる。Active, Passiveの両方の損失はノイズに強ければ、合成させてもノイズに強い。
なぜ学習不足に陥りづらくなる?
Normalizedすると、Cross Entropyの場合として、部分がそのままでも、他の(ラベルが他のクラスである、と置いた時の損失の値)が増加することがある。
特に、の部分は学習が進んでいたらが減るが、それとは別に他のが増える結果となっても全体の損失は下がる。しかし、当初の目的のを減らすにはならない。
最初のうちはちゃんとが増える以上にが減るので有益になるらしい。
なぜActive Passive Lossでは解決できる?
Normalized Passive Lossでは、「該当のラベルである」以外にも「該当しないラベルの確率も低くする」ので、これを通しておのずとも小さくしていくので、比較的に目的関数を減らす=を減らすというようにすることができる。
先行研究に比べて何がいいか
先行研究でもNLNLがあるが、10倍以上遅く3ステップ以上の複雑な訓練過程が必要である。
- 補ラベルで訓練する。
- 閾値を用いて信頼度の高い補ラベルで訓練する。
- 信頼度の高い普通のラベルで訓練する。
これはActive LossとPassive Lossで訓練することを交互にやっているといえるが、APLは明らかに良い。
実験
単純にNormalizedするとロバストになるが、性能は低下する
前述のようにNormalizedするだけでは意味がない。
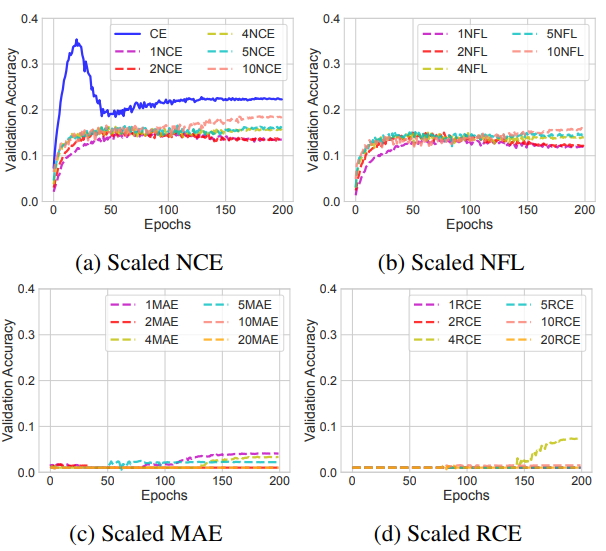
Normalizedしたものを数倍にスケーリングする意味はあるか
スケーリングはあまり意味がない。
CIFAR10では意味があるがこれは学習率を調整すればいいし、CIFAR100では意味がない。
APLの結果
十分に良いとわかる。
係数をそれぞれ変更したところ、より複雑なデータセットでは高い係数でのActive Lossと低い係数のPassive Lossが重要である。

