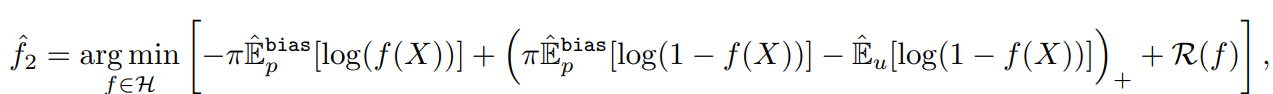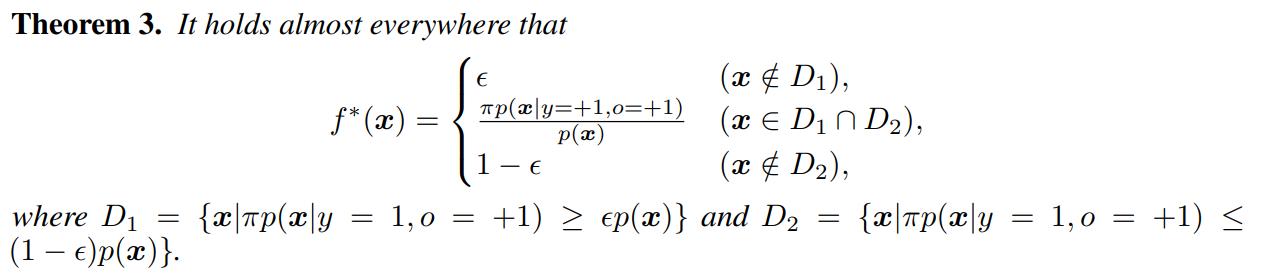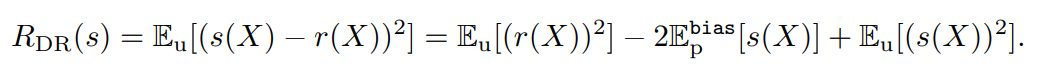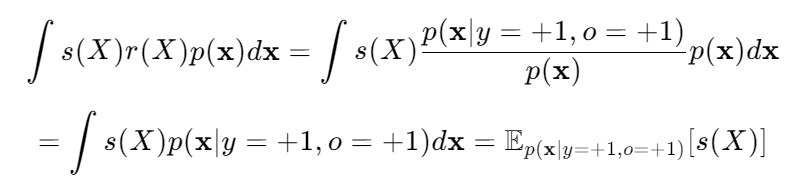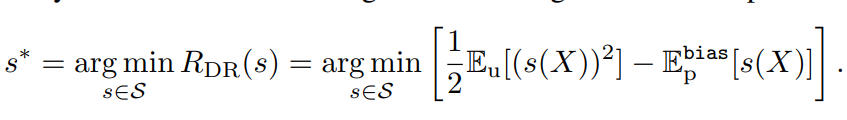https://openreview.net/forum?id=rJzLciCqKm
参考: 昔自分が書いた記事
Introduction
既存では、PU Learningの仮定はPositive例の中から一様にサンプルされる例が選ばれるSelect Completely At Random=SCARであった。だが、実際の応用では非現実的である。
これに対して、バイアスを考慮した研究がある。📄 2019-ECML PKDD-[PWE]Beyond the Selected Completely At Random Assumption for Learning from Positive and Unlabeled Data など。
2019-ECML PKDD-[PWE]Beyond the Selected Completely At Random Assumption for Learning from Positive and Unlabeled Data など。
この研究では、SCARではないが、もっと強い仮定を設けてそれについての研究を行う。簡単に言うと、よりPositiveの確度が高いほど、よりラベル付けされやすいという仮定。
問題設定
- サンプルはx∈Rd
- Ground-Truthのラベルはy=−1,+1
- ラベルがついているはo=+1であり、ついてないはo=0
- 本論文はCase Control。つまり、Pr(o=+1)はわからない。
- Positiveはp(x∣y=+1,o=+1)からサンプリングしている。
- Unlabeledはp(x)からサンプリングしている。
- SCARではないので、p(x∣y=+1)=p(x∣y=+1,o=+1)もあり得る。
- Class Priorπ=Pr(y=+1)は重要である。
📄 2017-MLJ-Class-prior Estimation for Learning from Positive and Unlabeled Data
2017-MLJ-Class-prior Estimation for Learning from Positive and Unlabeled Data
Identification Strategy
SARについての1つの仮説
SCARの場合、以下の条件が成り立つ。つまり、ラベルがつくかどうかによって、Ground-TruthがPositiveであるサンプルの事後分布には影響しない。
p(x∣y=+1,o=0)=p(x∣y=+1,o=1)=p(x∣y=+1) これを利用して式変形として以下のようなことができた。
SCAR仮定を外すと、最後の式変形のステップがこなせなくなる。このままではSARで行き詰まってしまう。
そこで、本論文は、Charles Manski. Partial Identification in Econometrics. Palgrave-Macmillan, 2 edition, 2008.のPartial Identificationから着想を得て、さらなる仮定を加えて、SAR設定で問題を解いていく。
∀i,j,Pr(y=+1∣xi)≤Pr(y=+1∣xj)⇔Pr(o=+1∣xi)≤Pr(o=+1∣xj) つまり、よりPositiveの確度が高いほど、よりラベル付けされやすい。
Related Work
省略
Partial Identificationと分類の戦略(提案手法)
直接Pr(y=+1∣x)の推定が難しい(Class Priorがあっても、選択バイアスがあるので)ことから、以下の分布の密度比を推定する。
r(x)=p(x)p(x∣y=+1,o=+1) 先ほど提案した仮定「よりPositiveの確度が高いほど、よりラベル付けされやすい」によれば、以下のことが成り立つ。
∀i,j,Pr(y=+1∣xi)≤Pr(y=+1∣xj)⇔r(xi)≤r(xj) 証明はこちら
左辺は推測できないが、順序を保っている右辺を推測することで左辺の代わりにしようというもの。r(x)を得た後、ある閾値θを設けて、識別器を以下のようにする。
先行研究では、データにラベルを付けられるデータ数に制約を設けて、最も密度比が高いサンプルにPositiveのラベルを付けるというかたちで選別していく。
h(x)=sign(r(x)−θ) ここで提案されているθの選択の手法は、以下の式である。累計密度関数は広義単調増加なので、適宜なところで二分探索して妥当なθ=θπを見つければよい。
π=∫1[r(x)≥θπ]p(x)dx この時、precisionはrecallとも同じになるらしい。これはprecision-recall breakeven point(BEP)というらしい。閾値決定の時にこういう条件が理想的である。
アルゴリズム
アルゴリズムの流れ
まず、指定のRisk Estimatorをもとに、r(x)を推定する。そこからθπを推定することで、識別器h(x)が完成する。
r(x)の推定
r(x)=p(x)p(x∣y=+1,o=+1) fから推定する。
r(x)を推定するための手法の1つとして、以下の式を用いるということ。通常のPUのリスクの式ではSCARの場合はPr(y=+1∣x)を予測できるが、こっちではPr(o=+1∣x)=Pr(y=+1,o=+1∣x)を予測するに過ぎない(ここの等式はPUでは必ずラベル付き)。
r(x)=p(x)p(x∣y=+1,o=+1)=p(x)Pr(y=+1,o=+1)p(x,y=+1,o=+1)=Pr(y=+1)1⋅Pr(y=+1,o=+1∣x) 📄 2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data では、以下のような損失の最小化が提案された。しかし、これはSCAR仮定で、バイアスに対しては何も考えていない。(これはl(g)−l(−g)=−xとすれば計算効率が上がるという論文だった)
2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data では、以下のような損失の最小化が提案された。しかし、これはSCAR仮定で、バイアスに対しては何も考えていない。(これはl(g)−l(−g)=−xとすれば計算効率が上がるという論文だった)
しかし、SAR仮定ではEP∼p(x∣y=+1)を得ることはできない。しかし、使えないと割り切っても同じ式をここでは使う。
ここでは、損失関数をl(f(x),+1)=−logf(x),l(f(x),−1)=−log(1−f(x))としている=Logarithmic lossである。
式に関しては、これ以外にも、📄 2017-NIPS-[nnPU] Positive-Unlabeled Learning with Non-Negative Risk Estimator で提案されていたnnPUの式も導入している(DNN用はこちら)。
2017-NIPS-[nnPU] Positive-Unlabeled Learning with Non-Negative Risk Estimator で提案されていたnnPUの式も導入している(DNN用はこちら)。
上のリスクを最小化するf∗を考える。∀ϵ∈[0,1/2]で以下の定理が成り立つ。
D1はラベル付きのデータの分布のπ倍が、
ようわからん。
直接r(x)を推定する
先ほどはPr(y=+1,o=+1∣x)を推定し、そこに1/π=1/Pr(y=+1)を掛けることで、r(x)を求めていた。
ここでは、直接推定する手法を考えてみる。ここでは、最小二乗法による重要度fittingを使っている。具体的には、s(X)という関数を使って、r(X)に近似していくことを考える。
−2s(X)r(X)の部分は、以下のように期待値を展開すると、別の期待値にすることができる。
定数部分を除くと以下の部分を最小化するのと等しい。
実験
実験ではモデルとして、
2019-ECML PKDD-[PWE]Beyond the Selected Completely At Random Assumption for Learning from Positive and Unlabeled Data など。
2017-MLJ-Class-prior Estimation for Learning from Positive and Unlabeled Data
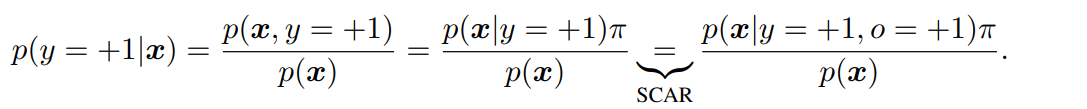

2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data では、以下のような損失の最小化が提案された。しかし、これはSCAR仮定で、バイアスに対しては何も考えていない。(これはとすれば計算効率が上がるという論文だった)
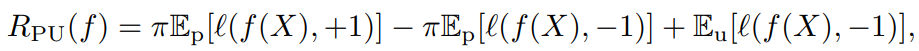
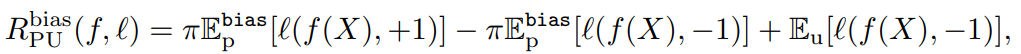
2017-NIPS-[nnPU] Positive-Unlabeled Learning with Non-Negative Risk Estimator で提案されていたnnPUの式も導入している(DNN用はこちら)。