https://arxiv.org/abs/1803.11364
後述の論文 📄2019-CVPR-[PENCIL]Probabilistic End-To-End Noise Correction for Learning With Noisy Labels ではこれよりも良いアーキテクチャを提案したとしている。
Introduction
この論文では以下のものを提案した。
- backbornのモデルに少し他の要素をつけていくアーキテクチャを提案した。
- DNNは高い学習率ではNoiseまで覚えにくいので、Memorization Effectとして簡単な特徴として覚えたい特徴だけ覚えられ、最後に覚えづらいNoiseが覚える形ではないか
Related Work
正則化、遷移行列によるものは次のSurveyで紹介されている。
📄2020-Survey-A Survey of Label-noise Representation Learning: Past, Present and Future
問題設定
- ハードラベルとは、one-hotのラベルであり、空間に属するとしている。
- ソフトラベルとは、合算したら1となるラベルであり、空間に属するとしている。
- 損失は以下のように、Noisyなラベルのハードラベルを対象としたクロスエントロピー損失。
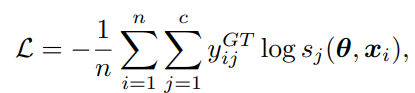
上の式はCleanな場合に使えばいい式だが、Noisy Labelの場合このまま学習するよりもより良い手法でやると提案できる。
提案手法
根本として、ラベルをうまく付け替えることで、いろんな正則化項をつけた損失関数の最小値を計算することに変わりはない。高い学習率で学習すれば、ノイズに適合させずに最適化できる。この時、モデル自体はある程度信頼できるものだと仮定すれば、与えられたNoisy Labelと合致したらCleanなラベルだと考えていい。
なお、ここではアルゴリズムの流れにあるように、事前にある程度パラメタだけ学習させるのではなく、同時にパラメタとラベルの学習を交互に行っている。
そしたら次は、
と、ラベルも更新を行っていく。
は以下のように構成する。
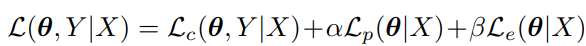
について
これはラベルと予測結果の近さを比較している(つまり普通の損失)。クロスエントロピーの代わりに、分布の近さを計算するKLダイバージェンスを用いた。
について
下記のアルゴリズムでは、どうやらすべて1つのクラスに属するようにラベル付け替えが行われてしまう。なので、事前にどのクラスがどれほどの割合で存在しているか?というのを事前情報として学び、のベクトルにまとめて、以下のようにKLダイバージェンスを計算して離れすぎないようにする。
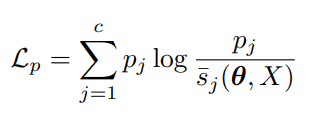
は各ミニバッチごとの各クラスの割合であり、随時更新される。
について
1つのクラスが突出して選ばれる分布にするように、Entropy Regularizationをかける。
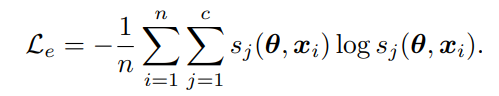
アルゴリズムの流れ

まずはパラメタを学習してから、次にラベルの学習を進める。1エポックの間で1回ずつこの順番で行う。ラベルの学習はソフト、ハードの2つのアルゴリズムがある。
ハードラベルの更新の場合、以下のように更新される。
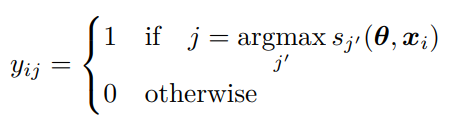
番目のサンプルの所属クラスは、先ほど更新した学習器の予測ラベルにする。
ソフトラベルの更新の場合、以下のように更新する。
つまり、そのまま予測器の出力で更新するか=ソフトラベル、その中で最大のものに属するとしてone-hotで更新するか=ハードラベル。
全体の訓練では以下の3ステップである。
- 損失関数はだけでまずAlgorithm1を計算する。
- 1によってCleanなラベルをまず求める。
- 得られたCleanなラベルを用いて、通常のクロスエントロピー損失で普通に学習する。
Co-Trainingともいえる?
Experimentとか
直系後続研究 📄2019-CVPR-[PENCIL]Probabilistic End-To-End Noise Correction for Learning With Noisy Labels にだいたい同じ方法でやっているので省略。
