https://papers.nips.cc/paper_files/paper/2016/hash/79a49b3e3762632813f9e35f4ba53d6c-Abstract.html
Introduction
PU Learningするには、Uの中に含まれているPとNの割合を知ることが重要である。
既存のClass Prior推定ではNoiseがある高次元のデータ(画像とか)を考慮していなかった。先行研究の多くはPの分布がわかるか、Pが十分にCleanであることが前提であった。
先行研究ではNoiseに対するアプローチはあるが、密度比推定が必要で、これは高次元データではうまく動かない。
この論文では、Noiseある高次元データについてのClass Prior推定の手法を提案する。入力されたデータをある単変量の分布に変換し、そこで密度比推定を行う(次元を落とすってことかな)。
問題設定
Noisy PUの問題設定を考える。
二値分類において、本来は以下のようにの割合で混合分布が与えられるデータであるが、Noisy Labelの場合は、とは違うがClass PriorであることでNoisy Labelを表現している。
この場合、f1, f0の分布自体が違ってくることを想定せず、ノイズはクラスやインスタンスに依存せずに発生すると仮定している。だいぶ限られたノイズパターン。
この問題設定において、うまくをNoisyな高次元データでも推定できるようにするのが目標。
Class Priorの推定
の2つの分布が与えられたときに、Class Priorは一意に定まるとまず仮定する。
実をいうと一般的にはがを含む、その逆もしかりとありえるので、実はこの過程は成り立たないこともある。
これを避けるために、できるだけを相方によってあらわせないようにしたい。これは相互不可約性という。
例えば、一様分布とガウス分布みたいな。
以下のように2つの混合分布を定義する。
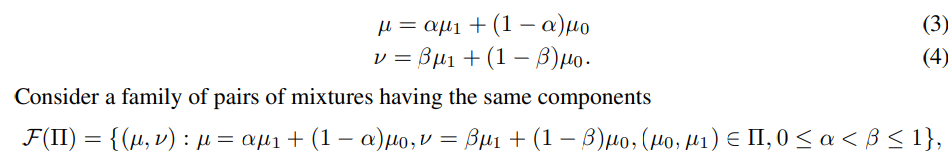
そして、この中での2つの基底の選び方は以下のように選べるすべての組み合わせのうち、全く同じ形以外のもので組み合わせの集合を考えられる。
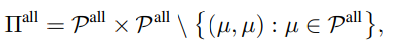
だが、は、同じガウス分布だけどパラメタが違うみたいなものを防げないので、一様分布とガウス分布による混合、みたいに明確に分布の形が違い互いに表せない必要があり、それはという集合とする。こっちのほうが大事。
つぎに、最大成分割合というものを定義する。これは、基底の分布が混入できる最大の割合だとする。
もし、ならば、一切はに混合されないということ。
最後に、基底の直積の集合、2つの混合分布を与えたとき、ありうる混合比率を構成する集合は、とおく。この集合は1つだけ要素を持てば、において識別可能つまり一意に特定できることを指す。
だが、ここで意外なことに、の要素を基底に使うと、識別可能ではないときがある。
説明
まず、混合分布が与えられたとする。ここから式(3), (4)の定義に従うと、以下のように基底となるが得られる。
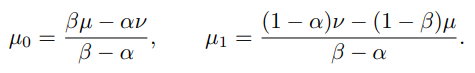
これらが集合上の測度として満たすには、どうやらを満たす必要があるらしい。(はαの最大成分割合、も同様)
だがこの条件を満たすとき、等式ではなく不等式なので明らかには一意に決まらない。
その代わりに、一意に定まるような条件を新たに、以下のように考える。
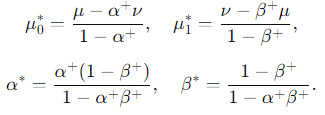
このようにおいたとき、から混合分布を生成すれば、ちゃんとClass priorは一意に決まるらしい。
問題設定
確率変数を入力の真の分布を表す値をとるランダム変数として、確率変数は真のラベルを表すランダム変数だとする。すると、に従い、が分布する(それはそう)。
ノイズについては、以下のように加える。
- 確率変数を各サンプルごとに考える。
- の時は、データセットから除外する。
- の時は、Unlabeledにする。
- の時は、Positiveとする。
- と真のラベルは必ずしも一致しないから、Positiveと言ってもNoisyなPositive(がNegativeであるものが混入するかもしれない)
PUのNoiseがある問題設定として以下の3つを追加で考える。
- Unlabeledの中のClass priorの値はデータセット全体のClass Priorと同じ。
- ラベルを付けるというの意味を持つ潜在変数を引いた時、実際にPositiveである割合は、全体の観測されたClass priorはと同じということ。
- 実際にであるようなのサンプルを引いたら、確率で誤ってPになってしまう、というかたちでNoiseが混入する。
- なお、の場合でも、すべてラベル付けされるということではなく、の確率で誤って、学習に使わない=データセットから除外される(の時のように)。
- 潜在変数は影響しない。
この3点を満たすならば、以下を満たす。
- このようにUnlabeledの分布はの分布と同じ。
- 除外するデータはありうる。
解き方
以下のような識別器を訓練する。
これをうまく予測することで、以下のように真のClass priorを計算できる。

具体的なアルゴリズム
ということで、前述のようにがわかり、がわかったならClass priorが推定できる。しかし、は以下のように定められている。ここで、の正確な推定が難しいということでもある。
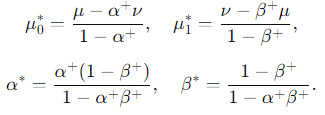
パラメトリック
ガウス混合モデルとみなして、すべてのパラメタを同時に推定できるらしい。しかし、これはモデルに実際データが十分フィットする前提。
ノンパラメトリック
AlphaMaxでを推定する。
